ML（6）——改进机器学习算法

　　现在我们要预测的是未来的房价，假设选择了回归模型，使用的损失函数是：

 

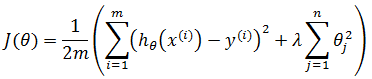
　　通过梯度下降或其它方法训练出了模型函数h_θ(x)，当使用h_θ(x)预测新数据时，发现准确率非常低，此时如何处理？

　　在前面的章节中我们知道，可以选择下面的一种或几种方案：

1. 获取更多的训练样本
2. 选择更少的特征集
3. 增加新的特征
4. 增加多项式特征（x₁x₂, x₂²…）
5. 增加正则化参数λ的值
6. 减小正则化参数λ的值

　　然而遗憾的是，这些方法在不同场景下的作用不同，有时毫无作用，在选择失当的时候甚至会出现反效果。当然不能凭直觉去选择改进方法，我们依赖的是一套被称为“机器学习”诊断法的方法。

模型评估

　　在改进机器学习算法之前先要知道模型的准确率，也就是对新样本的预测程度。即使模型对训练数据全部拟合，也不能证明模有较高的准确率，比如过拟合的时候：

　　也许可以通过作图法观察预测曲线是否存在过拟合线性，但这仅对特征较少的模型有效，大多数时候都无法作图。

留出法

　　有一种被称为“留出法”的方法可以帮助我们对模型做出评估。假设训练集有10个训练样本，为了确保能够过评估假设函数，我们将这些数据分成两部分：

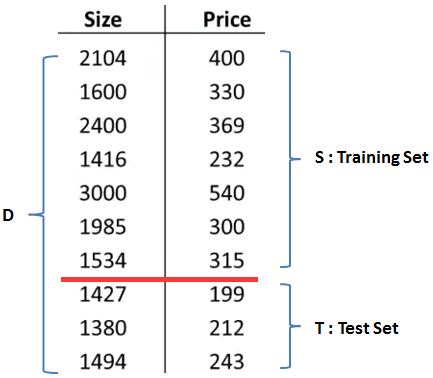
　　留出法将数据集D拆分成两部分，其中一部分S作为训练集，另一部分T作为测试集。这里D = S∪T， S∩T=φ。通常取S和T按照7:3的比例划分。需要注意的是，如果D的数据是排序的，在划分前需要打乱排序，也就是说训练集合测试集都要采用均匀抽样。

　　现在，在S上训练出模型h_θ(x)后，用T作为测试数据对泛化误差进行评估。我们已经知道怎样计算S上的损失值J(θ)，也叫做误差。现在要计算测试集上的J_test(θ)，这与J(θ)类似：

 

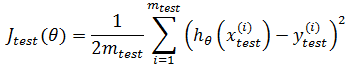
　　J_test(θ)越小，说明模型越好。对于分类，比如逻辑回归，也可以用同样的方法定义J_test(θ)，但是为了便于理解，通常使用“错误率”和“精确度”进行评估。如果T包含300个样本，如果用S训练模型后，T上有90个样本分类错误，那么错误率 = (90 / 300) * 100% = 30%，精度 = 1 – 30% = 70%

模型选择

　　我们的另一个任务是在众多模型中选出最好的那个。

　　现在我们要使用线性回归预测未来的房价，可选的模型集合是Μ = {M₁, M₂, …, M_d}，M的下标代表多项式的次数：

 

　　现在的问题是如何从M中选择最佳的模型？假设下图是其中三种模型的拟合曲线：

 

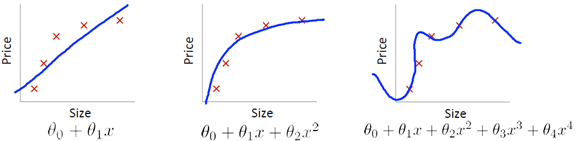
　　虽然d = 4拟合了全部数据，看起来学习的最好，但同时也产生了过拟合，从而失去对新样本的泛化性。

　　很自然地想到用上一节的留出法对M中的每个模型进行评估，先用训练集计算出模型函数，再根据模型计算出测试集上的J_test(θ)：

　　J_test(θ^(d))中θ的上标表示θ中除了θ₀之外分量的个数，这里也是多项式的次数。从中选取J_test(θ)最小的一个作为最佳拟合模型。这看起来没错，但实际上仍然不能很好说明模型泛化时的效果，因为我们选择的是能够最好地拟合测试数据的d的值，也就是说我们这是用测试集T去拟合多项式次数d。比如最后选取了d = 5作为最佳模型，然后用d = 5的模型去进行模型评估；由于d = 5已经是测试集T拟合得到的，再用T去做h_θ(x)的评估，很可能得到相当小的J_test(θ^(d))，但是对新的样本就没谱了。

　　需要注意的是，模型评估和模型选择是两个概念。留出法用于模型评估，可以对任意模型“打分”，但它并不总是适用于模型选择。

留出法的改进版

　　留出法也叫做简单交叉验证，其改进版可以帮助我们进行模型选择。它将数据集D划分为互不相交的三部分：训练集S，交叉验证集CV，测试集T，三者通常按照6:2:2的比例划分：

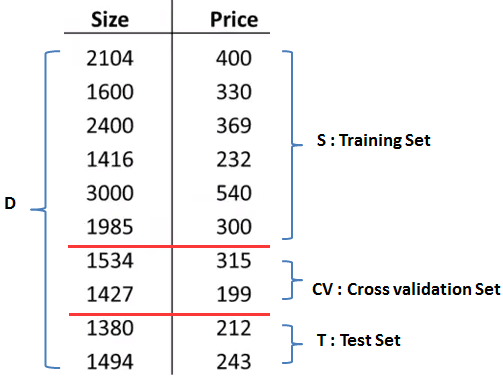
　　训练集、交叉验证集、测试集三者的误差：

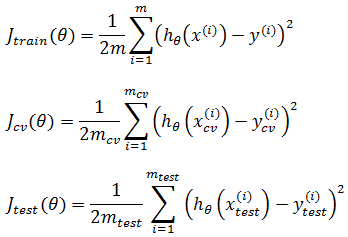
　　对于房价预测的模型选择问题，使用交叉验证处理，先用训练集计算出模型函数，再根据模型计算出交叉验证集上的J_cv(θ)：

 

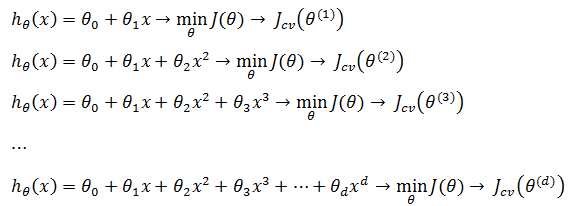
　　选择交叉验证集上误差最小的那个，以此确定多项式次数d的值，假设这里选择的是d=4：

 

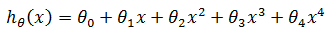
　　由于这个多项式次数并没有和测试集拟合，所以可以放心地使用测试集评估泛化误差。

k折交叉验证

　　先将数据集D划分为k个大小相似的互斥子集，每个自己都尽可能保证数据分布的一致性。轮流将其中k-1个子集作为训练数据，余下那个作为测试集，这样就可以获得k组训练/测试集。然后进行k次训练和测试，得出k个正确率或误差率，最终返回的是k个正确率或误差率的均值。K通常取10，称为10折交叉验证（10-fold cross validation）。

偏差和方差

　　如果一个机器学习算法不理想，多半会是两种情况，一种是欠拟合，另一种是过拟合，在这一节中，我们用交叉验证的知识重新审视拟合问题。

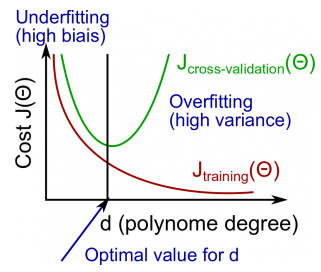
　　上面的例子已经见过多次，中图是较好的拟合，另外两幅分别对应欠拟合和过拟合。如果在训练时使用了交叉验证，那么误差和特征项次数的关系：

 

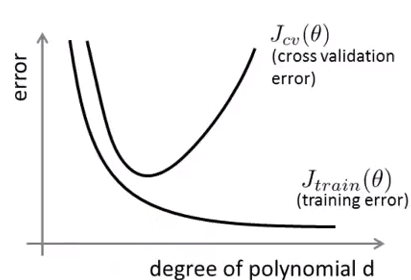
　　高偏差：J_train和J_cv都很大，并且J_train≈J_cv，二者都对应欠拟合，称之为高偏差（hign Bias）。可以理解为对任何新数据（不论其是否属于训练集），都有着较大的误差，偏离真实预测较大。

　　高方差：J_train较小，J_cv>>J_train，对应过拟合，称之为高方差（high Variance）。对于新数据来说，测试集误差有一个比较大的波动，因此说是高方差。

 

与正则化的关系

　　可以通过正则化来处理过拟合问题，比如在线性回归中加入正则化项（过拟合与正则化可参考《ML（附录3）——过拟合与欠拟合》）：

 

　　偏差与方差的作用之一就是能够指导如何放缩正则化系数λ。

 

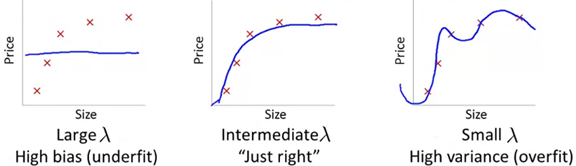
　　上面三幅图中都是在选择了4次函数d=4的基础上使用了正则化，图一的λ值很大，导致最终所有θ都接近于0，模型接近于一条直线；图二是大小合适的λ；图三的λ很小，几乎没起作用，导致模型过拟合。通过下面的步骤选择λ：

　　先通过交叉验证选择线性回归的次数，假设最终选择了d=4：

 

　　然后将损失函数中加入正则化项：

 

　　创建一个λ set， 例如λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}，对于每个λ，使用训练集训练后都将得到新的模型。根据新的模型计算测试误差和交叉验证误差，注意这里的计算测试误差和交叉验证误差不使用正则化项。最后选取最小的|J_cv - J_train|对应的λ为最佳结果，将该结果代入J(θ)_test，检验是否是合适的正则化项。

 

绘制学习曲线

　　当你想检查机器学习算法是否一切正常，或者你希望改进算法的表现，学习曲线就是一种很好的工具。绘制学习曲线可以帮助我们判断一个学习算法是否有高偏差或高方差问题。

　　本章开头提到了6种改进机器学习算法的方案，增加数据样本是其中的一种，那么样本数量和偏差与方差有什么关系呢？

　　假设在房价的例子中，我们选用直线作为假设函数，即h_θ(x) = θ₀ + θ₁x当样本很少时，得到一条直线拟合曲线，效果还算差强人意：

　　但是当数据增多时，无论如何调整直线，都会发生欠拟合：

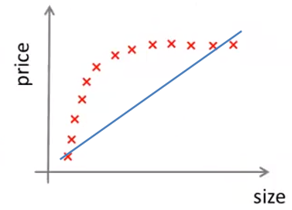
　　对于测试数据来说，由于h_θ(x)不够好，所以一开始就可能出现高偏差，此时，如果增加数据，测试误差最终会趋于平稳，但始终处于高误差状态：

 

　　 所以，如果算法处于高偏差（上图的蓝色曲线），增加数据量是没有意义的，因为训练数据已经发生了欠拟合，需要改变的是模型函数。一个模型可能成为好模型的前提是，在训练数据中不出现欠拟合。

　　相比之下，如果算法处于高方差，增加数据量将会对改进算法起到一定作用。假设我们使用了高次多项式和正则化得到了复杂的拟合曲线：

 

　　数据增加后，尽管拟合变得困难，但最终还是会得到一条复杂的过拟合曲线：

　　如果算法处于高方差，增加数据量会有所帮助，但随着曲线逐渐平稳，增加数据量对算法的帮助也越来越小：

 

　　所以说，当算处于高方差，或者测试数据的误差远远高于训练数据时，增加数据量是有所帮助的。

　　通过绘制学习曲线，可以回答本章开头的问题：

1. 获取更多的训练样本           high variance
2. 选择更少的特征集             high variance
3. 增加新的特征                 high bias
4. 增加多项式特征（x₁x₂, x₂²…）   high bias
5. 增加正则化参数λ的值         high variance
6. 减小正则化参数λ的值         high bias

误差分析

　　在使用机器学习算法解决一个实际问题时，因为缺少如何优化的指导方案，所以通常的做法不是事先选取一个复杂的“完美”模型，而是由一个能够快速实现的简单算法开始。在得到简单模型后，通过绘制学习曲线观察算法处于高偏差还是高方差，从而知道因该用哪种策略改进，比如增加或减少特征、增加数据量、增加或减少正则化系数等。对于算法的改进，还有一点可以做，就是误差分析。

　　所谓误差分析，就是将交叉验证集上拟合失败的数据收集起来重点分析，看看它们有哪些特征，针对这些特征对算法加以改进。

　　以垃圾邮件分类为例，如果在500个交叉验证集中有100封垃圾邮件被误判，那么可以针对这100封邮件进行分析，看看这些邮件是什么类型（药品推销、诈骗邮件、钓鱼还是其它），再分析一下这些邮件中有哪些特征可以对改进算法有所帮助。比如发现钓鱼邮件占了误分类的大多数，就需要重点对钓鱼邮件分析，看看钓鱼邮件中有哪些可供识别的信息；或者发现误分类邮件的标题或正文中有一些特殊的标点符号，比如一连串的感叹号，那么将这个特征提取出来作为垃圾邮件的特征或许是个有效的改进策略。

　　需要注意的是，误差分析并不能直接告诉我们某一种改进策略是否有效，只有经过修改后才能知道，比如通过词干提取能够将错误率从5%减低到3%，那么词干提取就是有效的方法，但是事先并不能知道，总之，先试试再说。

数据偏斜

　　在分类问题中可能会遇到这样一种情况，一类数据样本比另一类多很多，这种情况就称为数据偏斜。

　　比如使用二分类预测肿瘤病人是否患有癌症，但是全部数据集中仅有0.5%的病人真正患有癌症，数据向良性肿瘤一边严重偏斜。假设y=1表示患有癌症，此时设计了一个算法，最终在测试集上仅有1%的误差，那么这个算法是否是好的呢？在一个相对均衡的分类集上，这无疑是个很棒的结果，但是现在就不一定了，因为只需要简单的将预测算法全部返回0，就可以轻易将误差率减小到0.5%：

　　function predict(x)

         y = 0;

         return

　　上面的函数忽略了参数x，虽然预测的误差率下降到0.5%，但并不能说它是更好的预测。实际上我们可以遇到很多类似的问题，比如行人闯红灯是否会发生交通事故，买彩票是否会中奖。

查准率和召回率

　　为了应对数据偏斜，需要使用新的指标去评估算法，典型的是查准率（Precision）和召回率（Recall）。

　　仍然以癌症预测为例，如果实际结果和预测结果都为1时表示真阳性；实际结果为0，预测结果为1，表示假阳性；实际结果为1，预测结果为0，表示假阴性；实际结果和预测结果都为0，表示真阴性。这样一来数据集就可以切分为四方格：

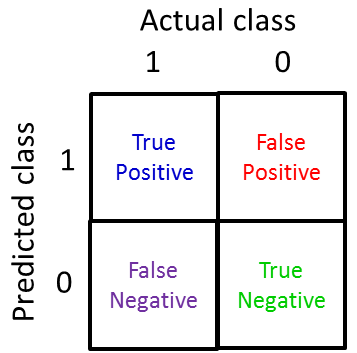
　　将1000个交叉验证集中的数据填充到方格中：

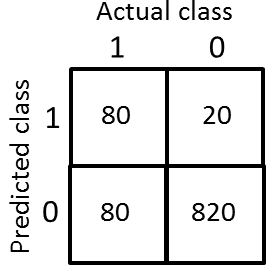
　　其中，查准率表示：预测为阳性（y=1）的数据中，有多大比率实际上也是阳性：

　　召回率表示：有多大比率正确预测了阳性的数据：

 

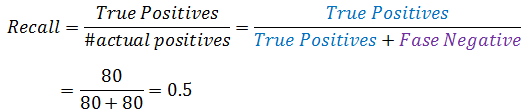
　　查准率和召回率范围在0和1之间，二者越大，表示算法越好。对于永远返回y=0的欺骗性算法，真阳性的方格中永远是0，所以召回率也是0。

如何选择

　　现在我们有了查准率和召回率两个指标来评估结果，那么以那个为准呢？

　　假设使用逻辑回归对进行癌症预测，h_θ ≥ 0.5时，预测结果为1，h_θ < 0.5时预测结果为0。告知一个病人患有癌症，对并病人是件痛苦的事情，所以现在想要对癌症的判断谨慎一点，为此我们稍微增大阈值，h_θ ≥ 0.7时，预测结果为1。此时可能得到一个比较高的查准率，因为对于所有预测为癌症的数据，有很大比率实际上就是癌症，相应地，也将得到一个比较低的召回率，如果继续调高阈值，二者的差距也将继续扩大。这样做未必合理，因为很可能漏掉实际上患有癌症的病人，从而错过了最佳的治疗时间。为了尽可能让不漏掉真正的癌症患者，需要调低阈值，此时得到了较高的召回率和较低的查准率。这实际上是两种思考问题的方法，没有明确的好坏之分。

　　在大多数实际应用中，我们希望查准率和召回率能够平衡。下面是三种算法的查准率和召回率：

 

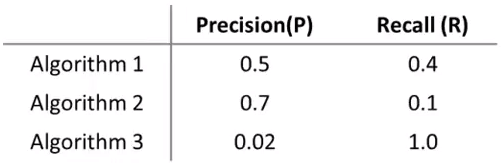
　　对于比较它们的好坏，很自然想到了均值法：

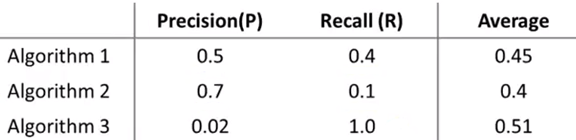
　　均值法判断算法3得分最高，这很明显是不对的，它几乎通知每个肿瘤患者都有癌症。由此可见均值法并不是有效的方法。

　　一种行之有效的方法叫F值法，也叫F₁值：

 

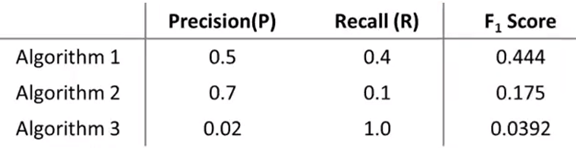
　　通过F值法，选择了最为均衡的第一种算法。

再看数据量

　　机器学习中有一句话：“取得成功的人不是拥有最好算法的人而是拥有最多数据的人”。可见数据量的重要性，然而事实未必总是如此。通常来说，数据量越多，训练出来的模型越不容易发生过拟合，但它的前提是特征向量x足够对结果做出预测；如果x的分量太少，即使数据再多，也不能对结果进行合理地预测，比如在对房价进行预测时，如果仅仅给出了房屋的面积，那么无法有效做出判断，因为影响房价的因素还有位置、楼层、房龄、是否学区房等。所以在判断一个问题能否使用机器学习进行预测时，可以首先问问人类的专家能否就已知条件进行预测，如果答案是肯定的，那么八成也可使用机器学习算法。

参考资料

　　Ng视频 《Advice for Applying Machine Learning》

　　《机器学习》周志华

　　《机器学习导论》

　　《机器学习》 Tom M. Mitchell

 

---

 　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”