ML（5）——神经网络3（随机初始化与梯度检验）

随机初始化

　　在线性回归和逻辑回归中，使用梯度下降法之前，将θ设置为0向量，有时会习惯性的将神经网络中的权重全部初始化为0，然而这在神经网络中并不适用。

　　以简单的三层神经网络为例，将全部权重都设置为0，如下图所示：

 

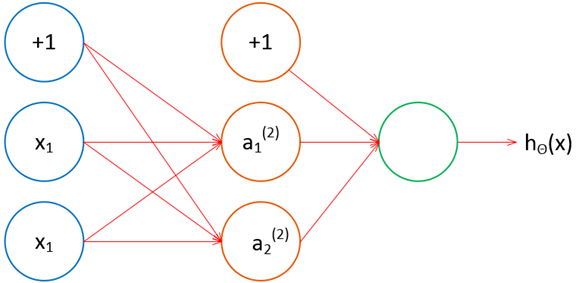
　　假设仅有一个训练数据，使用梯度下降，在第一次迭代时：

 

 

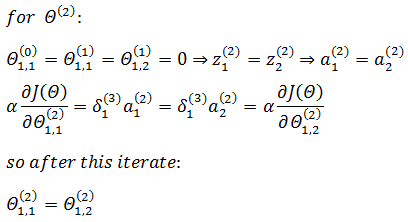
　　可以看到，第一次迭代的结果是：隐藏层的权重和激活值全部相等，输入层的权重相当于所有输入项放缩了相同的倍数。

　　在第二次迭代时：

 

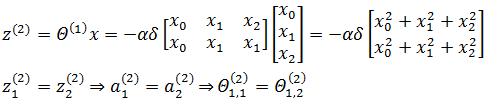
　　此时，隐藏层的激活值又一次全部相等。继续迭代也会得到相同的结果，即a⁽²⁾的所有激活值和权重都一样，这显然不是我们期待的结果。

　　为了应对上述问题，我们使用一种被称为“随机初始化”的方法去初始化神经网络的权值，具体来说，就是将所有权值在一个范围内赋予随机值，通常这个范围取[-1, 1]。下面是代码示例：

 Octave:

init_epsilon = 1;
Theta1 = rand(10, 15) * (init_epsilon * 2) - init_epsilon;
Theta2 = rand(1, 10) * (init_epsilon * 2) - init_epsilon;

Python:

import numpy as np

init_epsilon = 1
theta1 = np.random.random((15,10)) * (init_epsilon * 2)  - init_epsilon
theta2 = np.random.random((10,1)) * (init_epsilon * 2)  - init_epsilon

梯度检验

　　反向传播算法很高效，但对梯度的求解异常繁琐，实际上，即使某处代码计算出错误的梯度，仍然会得到一个模型，尽管这个模型的J(Θ)很小，但对新数据的拟合非常差，此时不得不重新审视所有代码。

　　是否可以从一开始就知道梯度是否正确呢？答案是肯定的，这就是梯度检验法。

　　梯度检验法是通过一种简单的方法取得近似的梯度，将这个近似的梯度与真正的梯度对比，如果很接近，则认为梯度正确，否则认为梯度有误。

　　将J(θ)和θ放入直角坐标系，下图所示是θ取定值时J(θ)的导数：

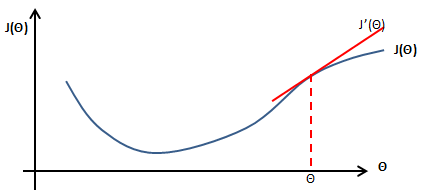
　　ε 是一个很小的值：

 

　　如上图所示：

 

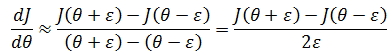
　　当ε→0时，这趋近于导数的定义：

 

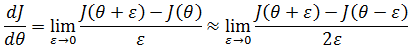
　　我们也不希望ε太小，通常取ε = 10^-4较为合适。

　　假设J(θ) = θ³，θ = 1，ε = 0.01，则：

　　如果J(θ) = J(θ₁, θ₂, …, θ_n)，则θ_j 的偏导：

 

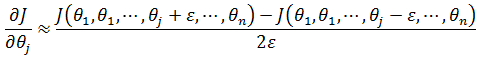
　　需要注意的是，梯度检验是数值计算，其代价远远高出能够使用向量矩阵计算的反向传播，所以一旦确认算法无误，就应当关闭梯度检验。

 数据拟合

　　隐藏层节点越多，层数越多，神经网络的规模越大。在数据拟合上，神经网络的规模越大，拟合效果越好。

　　上图的三个神经网络解决的是同样的二分类问题，后两个的规模要大于第一个。需要注意的是，随着神经网络规模的增大，计算量也大大提高，同时更容易出现过拟合。在出现过拟合问题时，可以尝试调整正则化系数。关于正则化，可参考《ML（附录3）——过拟合与欠拟合》

 

---

 　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”