ML（5）——神经网络2（BP反向传播）

　　上一章的神经网络实际上是前馈神经网络（feedforward neural network），也叫多层感知机（multilayer perceptron，MLP）。具体来说，每层神经元与下一层神经元全互联，神经元之间不存在同层或跨层连接；输入层神经元仅接受外界输入，不进行函数处理；隐藏层与输出层包含功能神经元，对信号进行加工；最终结果由输出层神经元输出。“前馈”是说网络拓补结构上不存在环路或回路，而不是指网络信号不能向后传递。

前向传播(FP)

　　所谓前向传播，就是根据一些列包含偏置项的权重矩阵Θ和输入层向量x，根据激活函数逐层计算，最终计算到输出层，得到输出结果的过程。

　　输入：总层数L，所有隐藏层和输出层对应的权重矩阵Θ，输入向层量x

　　输出：输出层的向量y

学习策略

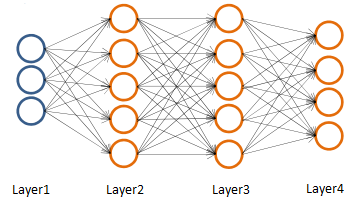
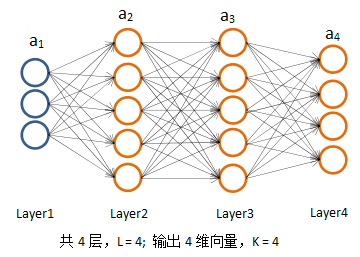
　　首先为下面的4层多分类神经网络定义一些符号。

 

• 训练样本：{ (x⁽¹⁾, y⁽¹⁾), (x⁽²⁾, y⁽²⁾), ……, (x^(m), y^(m)) }
• 神经网络层数： L
• 每一层的神经元数：S_l 下标l 表示神经元所在的层数，S_l 不包括偏置项
• 输出层的维度：K，由于输出层的神经元数=输出层的维度，所以 S_L = K。K=1表示二分类，K≥3表示多分类，K = 2没有意义（K=1已经是二分类，没有必要再添加一个输出神经元）。

　　上图中：

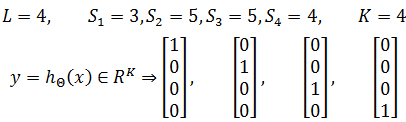
　　我们已经知道逻辑回归的损失函数：

　　上面的损失函数加入了正则化。由于神经元使用了sigmoid函数作为损失函数，所以神经网络的损失函数：

 

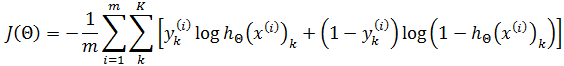
　　其中y⁽ⁱ⁾_k 表示第i个样本在输出层第k个维度的值。例如：

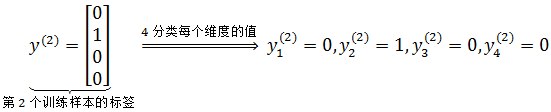
　　每个输出神经元的损失函数都和逻辑回归的类似。如果是单个神经元，即K=1时，正是逻辑回归的损失函数：

单个神经元

　　对于多分类，比如上面的4分类，逻辑回归首先对训练样本的进行预处理，根据分类不同，得到4组相同输入但标签不同的训练样本；然后使用相同的损失函数对每组样本进行训练，得出4个不同的h_θ；最后取置信度最高的h_θ作为预测结果。而神经网络只需要对训练样本进行一次预处理，训练后得到唯一的h_Θ。

　　神经网络的正则化项是所有隐藏层和输出层上所有神经元的正则化之和：

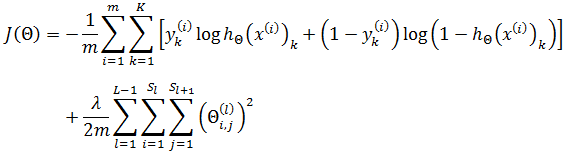
　　这里J(Θ)是一个实数。对于正则化项，L - 1是因为输出层作为最末层，不再继续向后传播。正则化同样不计算偏置项，所以Θ的下标从1开始。S_l 是第 l 层神经元的个数。以上面的4分类神经网络为例，L = 4：

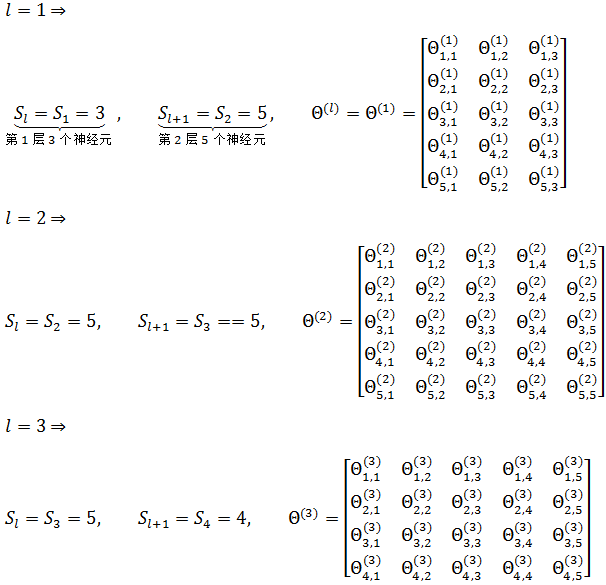
算法——反向传播(BP)

　　神经网络的学习过程就是根据训练数据来调整神经元之间的权值，通过权值可以计算出该层神经元的阈值，换句话说，神经网络学到的东西，蕴含在权值和阈值中。

　　我们的目的是找到最佳的Θ使得J(Θ)最小化，将求解Θ转换为最优化问题，即：

 

　　依然可以使用梯度下降：

 

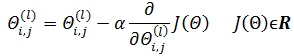
　　这里需要对Θ求导，然而实际推导时会发现，求导的过程远比逻辑回归困难。我们的求导目标：

 

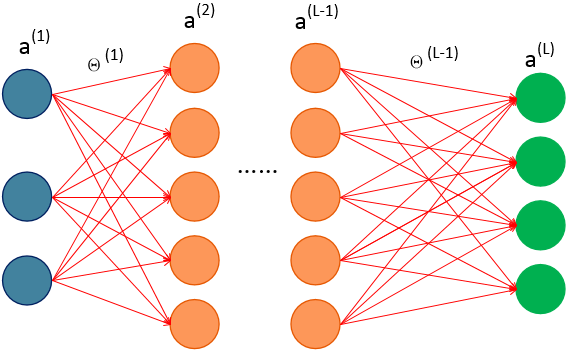
　　以下图为例，尝试进行反向传播的推导：

 

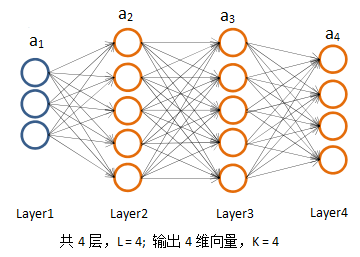
　　简单起见，将J(Θ)的正则化项去掉，并令m = 1，即仅有一个训练样本，此时可以去掉上标并固化一些参数：

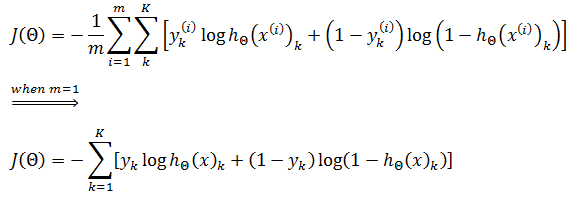
　　通过上一章的内容，我们知道，每一层的节点都依赖于上一层的节点和权重：

　　g是激活函数，这里是sigmoid函数。可以通过z和Θ之间的关联使用链式法则，对Θ_i,j^(l)求偏导：

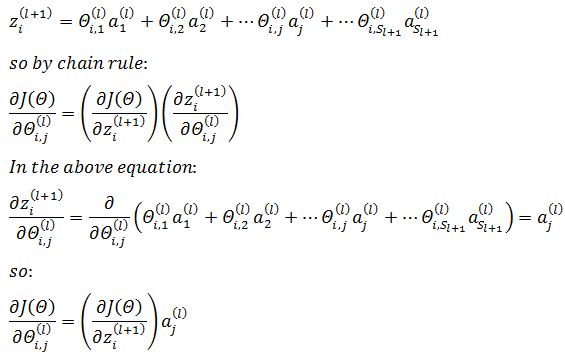
　　现在来重新审视一下J(Θ)的意义，它代表神经网络函数与实际结果的误差，也就是输出层与实际结果的误差，输出层的误差又来源于上一层……就这样从输出层开始，层层追责，直到输入层为止，这也是被称为“反向传播”的原因。

　　由于神经网络每一层有多个神经元，所以每层的误差又是由该层所有神经元的误差组成。对某一神经元的输入加以扰动就能获得该神经元对最终结果的影响，因此定义第 l 层第 j 个神经元a_j^(l)的误差是：

 

　　写成向量形式：

　　因为定义了神经元的误差项δ作为中间变量，所以：

 

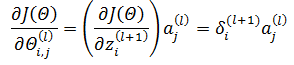
　　l 层的所有权重的偏导可以表示为矩阵：

 

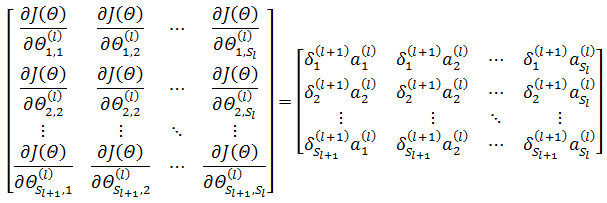
　　上式等于下面的简化形式：

 

　　注意这里Θ^(l)是S_l+1×S_l的矩阵，需要使用矩阵求导公式（y是标量，X是矩阵）：

 

　　最后的结果是一个矩阵，矩阵中的每一个元素都对应神经网络中的一个权重，算法的训练目标正是求得最佳权重。a^(l)可以通过输入层和初始权重求得，现在的问题是如何求解误差项δ。

输出层误差

　　输出层的误差可以直接用真实值和预测值的差值定义：

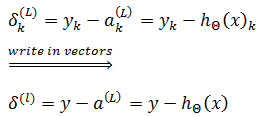
隐藏层的误差

　　对于隐藏层 l 层来说，它的某一神经元节点与 l+1 层的所有神经元都存在关联，如下图所示：

　　目标是计算 l 层的某个输入对最终结果的影响，即：

 

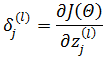
　　这里需要使用多变量微积分的链式求导法则，首先将z_j^(l)关联的节点参数化：

 

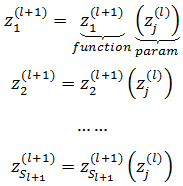
　　其中等式右侧的z_i^(l+1)是一个有唯一自变量z_j^(l)的函数，具体来说，是 l 层神经元的加权和。根据链式求导法则：

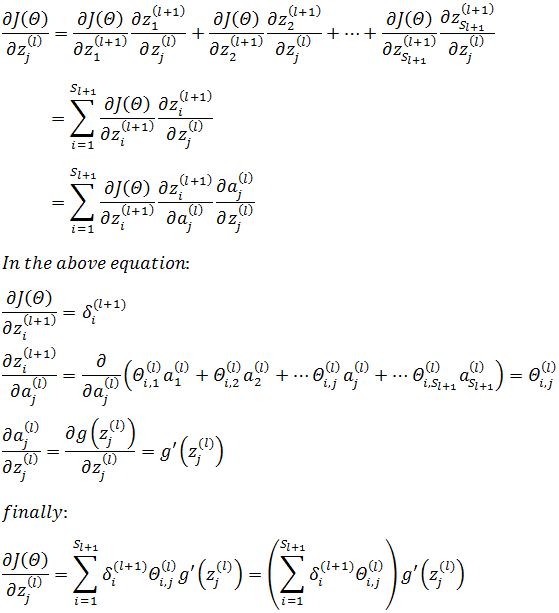
　　关于上式中多变量微积分的链式求导法则，可参考《多变量微积分笔记4——全微分与链式法则》。需要注意下标 i 和 j 的切换。是sigmoid函数，如果继续计算g’：

 

　　推导过程可参见《ML（4）——逻辑回归》。

　　用向量表示误差：

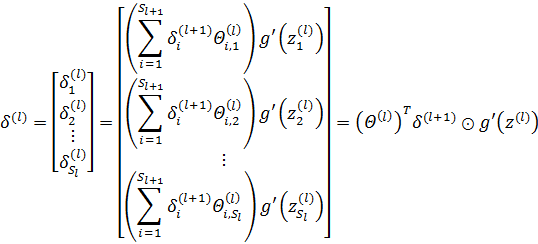
　　⊙表示矩阵的对应元素两两相乘，相当于Octave中的“./”操作。以下面的四分类为例：

　　

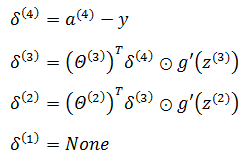
　　在写这篇文章时，本来想直接从网上copy一些推导，但是仔细阅读后，发现大多数网文直接将误差的推导写成下面的形式，最后莫名其妙地得出了结论：

 

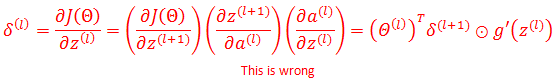
　　实际上这是错误的，对于矩阵或向量的求导无法直接使用标量函数的链式求导法则，即使能够像上面那样使用，也不会得到最右侧的结果。

正则化项

　　正则化项的求导较为简单，可以直接得出结果：

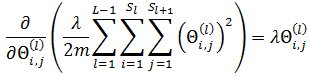
最终结果

　　现在，困难的求解过程已经结束，最初的目标已经能够求解：

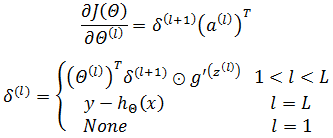
　　注意这里的约束条件是 1 < l，因为输出层没有权重：

　　扩展到m个训练样本，上标 t 表示第 t 组数据：

 

　　如果加入正则化项：

 

　　最终的梯度下降公式：

 

计算过程

　　根据梯度下降算法，需要反复计算权重的偏导，这在逻辑回归中很容易，但在神经网络中就比较麻烦，下面是权重偏导的计算过程：

　　1.训练数据：{(x⁽¹⁾,y⁽¹⁾), (x⁽¹⁾,y⁽¹⁾),…, (x^(m),y^(m))}

　　2.将所有权重初始化，设Δ_i,j^(l)是m个训练数据中所有相同位置的权重和，即：

　　3.开始训练，t = 1 for t to m:

　　　　3.1. set a⁽¹⁾ = x⁽¹⁾

　　　　3.2. 用前向传播方法计算每一层的神经元输出，即a^(l)

　　　　3.3. 计算每一层的误差，需要注意的是输出层和隐藏层的区别：

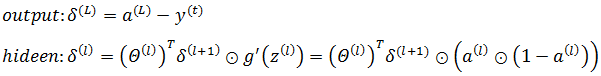
　　　　3.4.  累加Δ_i,j^(l)：

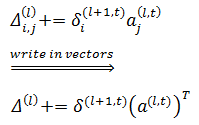
　　4. 求得权重的偏导：

　　注意D^(l)是一个包含 l 层所有权重偏导的S_l+1×S_l矩阵。

 

　　参考：

　　Ng视频《Neural Networks》

　　《机器学习》周志华

　　《视觉机器学习20讲》

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”