ML(5)——神经网络1(神经元模型与激活函数)
上一章介绍了使用逻辑回归处理分类问题。尽管逻辑回归是个非常好用的模型,但是在处理非线性问题时仍然显得力不从心,下图就是一个例子:

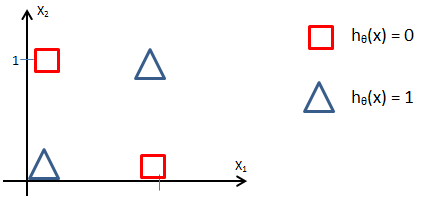
线性模型已经无法很好地拟合上面的样本,所以选择了更复杂的模型,得到了复杂的分类曲线:
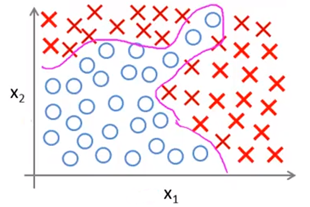
然而这个模型存在两个问题:过拟合和模型复杂度。过拟合问题可参考《ML(附录3)——过拟合与欠拟合》,这里重点讲模型复杂度。
还是非线性分类,现在将输入扩充为100个,为了拟合数据,我们构造了更多的特征:
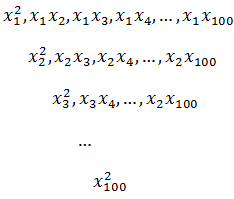
约有 1002/2 = 5000个特征。由此看来,对于n个输入,二次项特征的个数大约以n2/2的数量级增长,在真实世界中面临的输入何止成千上万个,此时将得到噩梦般的模型。
在计算机视觉中,几何数量级的特征无处不在:

如上图所示,虽然人眼能够马上识别出图片是汽车,但是机器就没那么容易,它所看到的仅仅是像素的矩阵。假设仅抽取汽车轮毂和方向盘上的两个点判断图片是否是汽车:
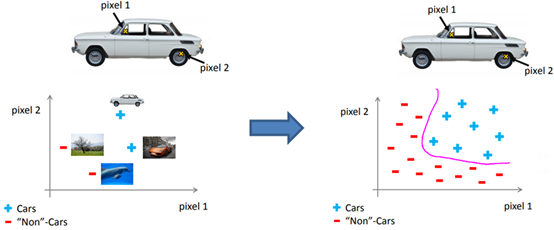
右图中得到了一个非线性曲线。实际上,即使仅有50 × 50的灰度图片,也会有2500个输入值;如果使用全二次项构造特征值,会产生 25002/2 ≈ 3000,000个特征值。由此看来,只是简单的增加二次项或者三次项之类的逻辑回归算法并不是一个解决复杂非线性问题的好办法,因为当n很大时将会产生非常多的特征项。
神经网络就是在解决复杂非线性分类问题上的一种好得多的算法,即使输入的特征维数n很大。
神经网络
1997年世界上发生过两件大事,一是克隆羊多利诞生,另一件是IBM 电脑“深蓝”击败国际象棋世界冠军。就在这一年,我从一本电子游戏杂志上看到了一篇关于计算机不可能战胜职业围棋选手的文章。
二十年过去了,2016 年一月底,谷歌在自然杂志上正式公开发表论文,宣布其以深度学习技术为基础的电脑程序 AlphaGo,在 2015年 十月,连续五局击败欧洲冠军、职业二段樊辉。这是第一次机器击败职业围棋选手。
在这篇文章中,我尝试介绍深度学习的前身——神经网络。
神经元模型
神经元是神经网络中的一个重要概念。其实我觉得,神经网络和神经元都是看似高逼格的名词,这让我们联想到脑神经,从而心生畏惧。我们经常看到下面的图示:
我想说,把脑神经都丢到垃圾桶里吧!
然而我们还是需要知道什么是神经元,如下图所示:
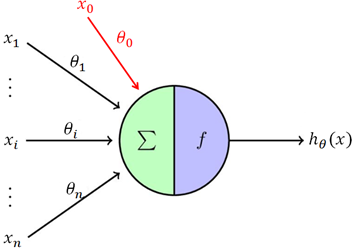
可以把这个神经元看作感知器模型:
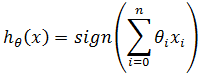
这是一个特殊的有向图,θ称为权重,x0称为偏置项,函数f是激活函数。在感知器模型中,激活函数是sign;在逻辑回归中,激活函数是sigmoid。
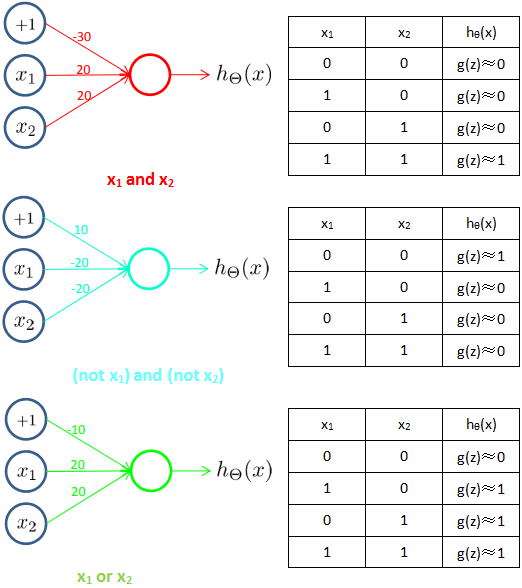
上图的神经元模型似乎有点类似数字电路中的电路门,实际上神经元模型确实可以实现一些电路门运算:
神经网络模型
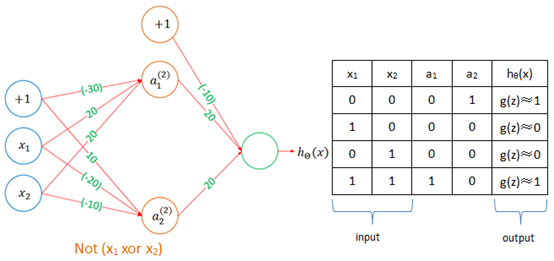
单个神经元模型和感知器模型没什么区别,对非线性分类有些力不从心,比如“异或否(not (x1 xor x2))”的判别:
这就需要使用多层神经网络:
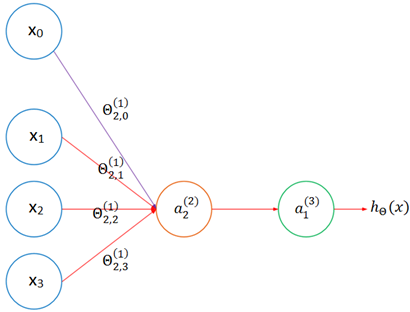
一个典型的神经网络如下图所示:
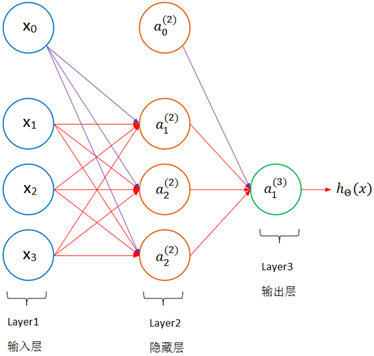
上图是一个三层神经网络,分为输入层、隐藏层和输出层。在隐藏层中,不能通过训练样本观测到节点的值。上图神经网络中有3个输入节点(偏置节点不计在内,通常也不单独画出),3个隐藏节点(偏置节点不计在内)及一个输出节点。
节点的上标表示神经网络的层数,a(2)表示第二层的节点,下标表示节点的序号,包括x0在内,所有偏置节点的序号都是0,值都是1。用大写的Θ表示每一层的权重,第一层的权重是Θ(1)。每个隐藏节点连同它的输入和输出,可看作一个神经元模型,由此:
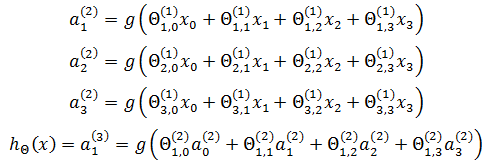
权重的下标分为两部分:第一部分表示指向该权重指向的隐藏节点的序号,第二部分表示权重的序号。Θ2,3(1)表示该权重处于第一层,它是指向a2(2)节点的第3个权重。可以将a2(2)单独列出:
如果神经网络的第j层有Sj个节点,第j+1层有Sj+1个节点,那么第j层权重Θ(j)的权重总数是 Sj+1×(Sj+1 + 1), +1是因为计算了偏置节点。
现在尝试用矩阵表示上面的神经网络模型:
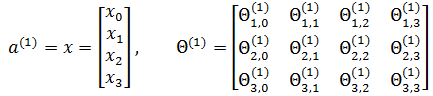
第一层节点x表示输入向量,Θ(1)表示第1层的权重。现在,用z(l)表示第 l 层的输入:
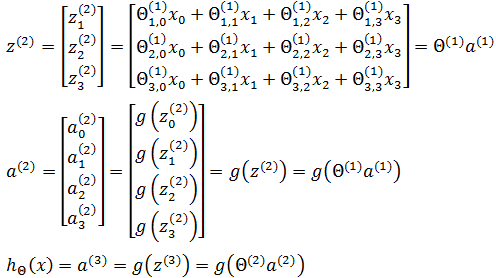
神经网络可以有多个隐藏层,每一层都会计算出更复杂的特征,但只有一个输入层和一个输出层:

激活函数
激活函数的作用是给神经网络加入一些非线性因素,使得神经网络更好地解决较为复杂的问题。
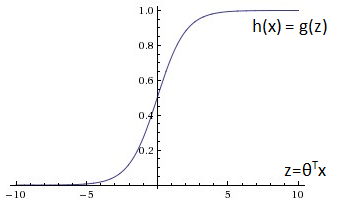
常见的激活函数是sigmoid函数,在《ML(4)——逻辑回归》中介绍过,还有很多其它的激活函数。
如果使用sigmoid作为激活函数,其区间是[0,1],当神经元的输出为1时,表示该神经元被激活,否则称为未被激活。类似地,如果激活函数是双曲正切tanh,其区间是[-1, 1],当神经元输出为1是表示激活,-1表示未被激活。
本节其余部分转自 https://www.cnblogs.com/dudumiaomiao/p/6014205.html
传统神经网络中最常用的两个激活函数,Sigmoid系(Logistic-Sigmoid、Tanh-Sigmoid)被视为神经网络的核心所在.从数学上来看,非线性的Sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在信号的特征空间映射上,有很好的效果,通过对加权的输入进行非线性组合产生非线性决策边界.从神经科学上来看,中央区酷似神经元的兴奋态,两侧区酷似神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区,将非重点特征推向两侧区.
Relu函数为现在深度学习使用比较广泛的激活函数,相比前面两个,其优点在于计算简单,导数简单,收敛快,单侧抑制 ,相对宽阔的兴奋边界 ,稀疏激活性;缺点在于在训练的时候,网络很脆弱,很容易出现很多神经元值为0,从而再也训练不动.一般将学习率设置为较小值来避免这种情况的发生.
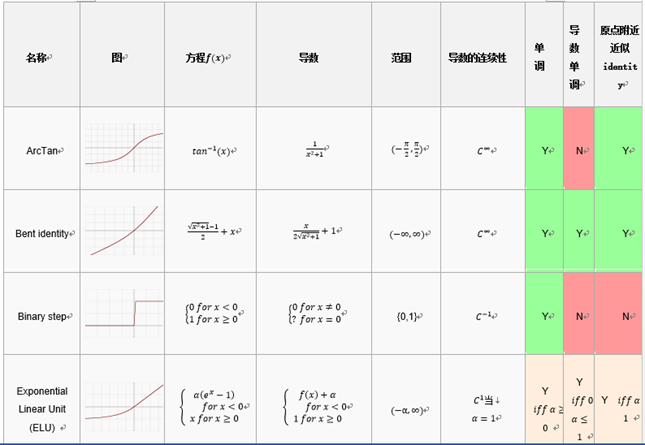
比较:
激活函数的一些可取的属性包括:
非线性:当激活函数是非线性的,然后一个两层神经网络可以证明是一个通用函数近似值.而identity激活函数不满足这个属性.当多层网络使用identity激活函数,整个网络就相当于一个单层模型.
连续可微的:这个属性对基于梯度优化方法是必要的.二进制激活函数在0点没有可微性,它在其他值上全部可导为0,基于梯度优化方法对于它毫无进展.
范围:当激活函数的范围是有限的,基于梯度的训练方法往往更稳定,因为模式显著影响几个有限权重.当范围是无限的,训练通常更有效率,因为模式显著影响大部分权重.在后一种情况下,较小的学习利率通常是必要的.
单调:当激活函数是单调时,与单层模型相关的错误表面是凸的.
平滑性:有单调导数的平滑函数已经被证明在某些情况下推广地更好.这些属性表明这些激活函数和Occam's razor更一致.
原点附近近似identity:当激活函数有这个属性,对于小的随机值初始化权重,神经网络将有效地学习.当激活函数没有这个属性,在初始化权值必须使用特殊例子.在下面的表中,激活函数,表明有该属性




多分类
神经网络也可以处理多分类。现在我们有一个能够区分行人、小汽车、摩托车和货车的四分类神经网络,如下图所示:
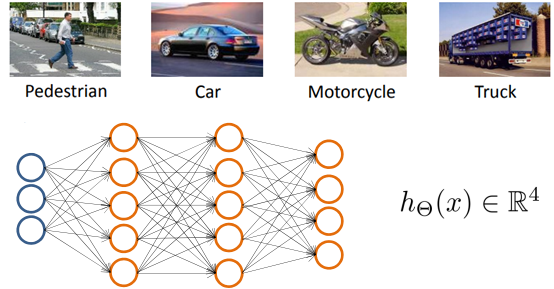
输出层在这里有四个节点,其基本思路和上一章《逻辑回归》的多分类一致,但是对输出需要稍加变动:
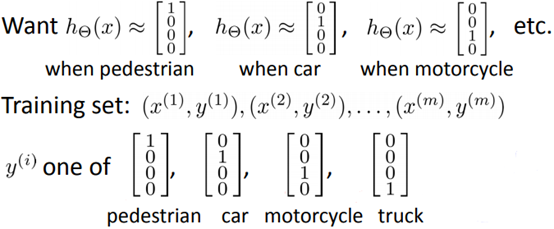
如果输出结果是<0, 1, 0, 0>,则判断图片是小汽车。
参考:
Ng视频《Neural Networks》
《数学之美》第二版
《集体智慧编程》
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号