多变量微积分笔记24——空间线积分
线积分或路径积分是积分的一种。在数学中，线积分的积分函数的取值沿的不是区间，而是特定的曲线，称为积分路径。在物理学上，线积分是质点在外力作用下运动一段距离后总功。
如果把空间向量场F = Pi + Qj + Rk看作力场，C是质点在力场作用下移动的曲线，那么C在力场中线积分就是质点在力作用下所做的功：
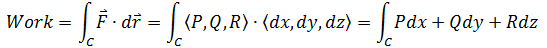
与平面向量场中的线积分类似，空间线积分在dr中多了分量dz。关于平面场中的积分，可参考《多变量微积分13——线积分》
计算空间线积分
和平面向量场的线积分一样，要用某个单变量参数转换x,y,z,最终使空间线积分转换成普通的一元积分。
示例1：
F = <yz, xz, xy>，运动轨迹C：x = t3, y = t2, z = t, 0 ≤ t ≤ 1，计算C的线积分。
先根据C的参数化计算dx,dy,dz：
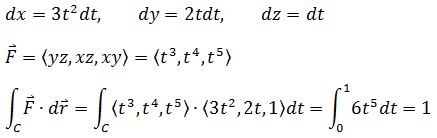
示例较为简单，但是对于没有明确给出的参数化，就需要自己判断如何简单有效地参数化。
示例2：
计算C的线积分，F = <yz, xz, xy>，运动轨迹C由C1，C2，C3组成，如下图所示：
C1，C2在xy平面，所以z = 0，dz = 0
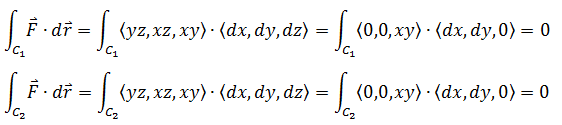
对于C3，x = 1, y = 1, dx = 0, dy = 0；0 ≤ z ≤ 1
独立路径
在《多变量微积分14——保守场和独立路径》中介绍了平面梯度场中线积分的独立路径：在梯度场中，如果需要计算一个线积分，无论怎样的路径，积分值都只跟起点P0和终点P1的值有关。
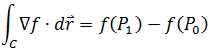
这对于空间向量场的线积分同样适用。在上节的示例2中，F = <yz, xz, xy>，很容易看出，f = xyz，F = ▽f = <yz, xz, xy>，因此向量场是保守场：
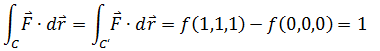
在保守场中，由于起点和终点一致，所以C的线积分和C’一样，f是向量场的势函数。
梯度场的判别
如果存在下面的关系，则表明空间向量场是保守场：
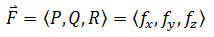
现在的问题是需要寻找到一个有效的方法判断场是否是保守场。这个方法基于一个事实，对于混合二阶导数，求导次序改变，其结果不变：
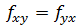
因此，如果场是保守场，则：
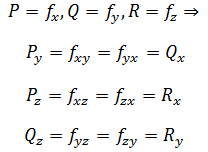
也可以用微分的观点来看待这个问题，如果f是保守场的势函数，则：
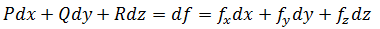
示例
如果axydx+(x2+z3)dy+(byz2-4z3)dz是保守场，a,b的取值是什么？
如果习惯使用PQR，可以将问题转换为Pdx + Qdy + Rdz，P = axy, Q = x2+z3 , R = yz2-4z，如果是保守场，则：
找出势函数
在《多变量微积分15——梯度场和势函数》中介绍过两种方法求解平面梯度场中的势函数，空间梯度场仍然可以使用这两种方法。
在上一节的示例中我们知道，F = <2xy, x2+z3, 3yz2-4z3>是梯度场，现在我们尝试找到它的势函数。
线积分法
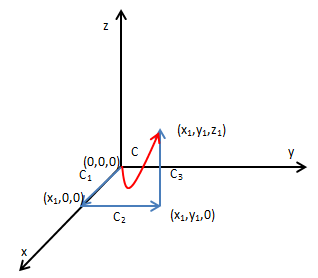
在梯度场中线积分的轨迹C从原点开始，终点是(x1, y1,z1)。根据独立路径的原理，梯度场中的线积分只和起点终点有关，和路径无关，所以可以寻求更简单的计算方法，将C拆分为C1,C2,C3如下图所示：
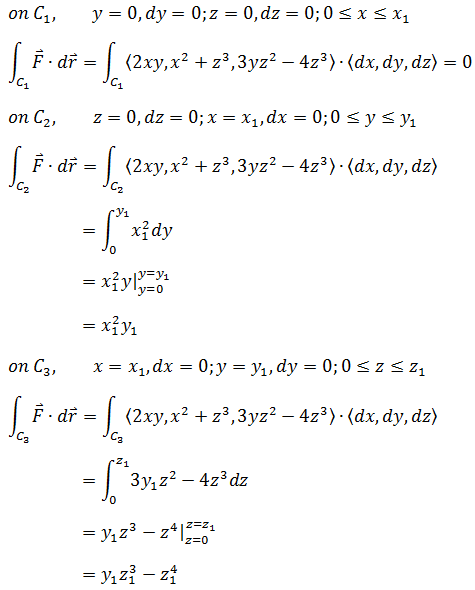
根据独立路径准则：
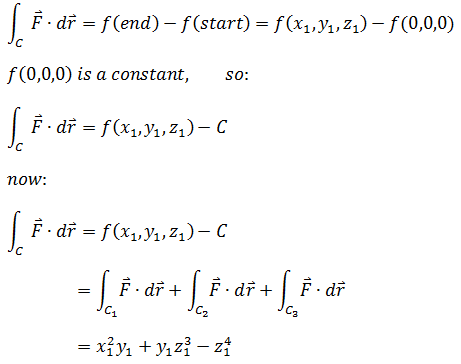
将xyz的下标去掉，就得到势函数：
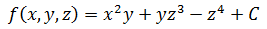
这里C是一个常数，说明f是一个势函数族，就像不定积分要加上常数C一样。
验证：
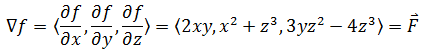
不定积分法
梯度场中的势函数f满足：
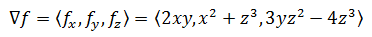
根据微积分基本定理，导数的积分等于原函数，这里将y,z看作常数，对fx求x的积分：
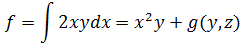
由于fx是偏导，所以积分最后并不是加上常数C，而是一个关于y和z的函数g(y,z)。
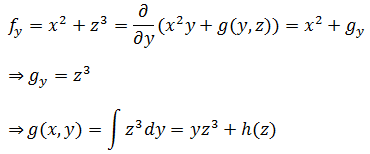
这里的常数是关于z的函数h(z)。现在：
综合示例
示例1
空间向量场F = zxi + zyj + xk，螺旋线C可参数化为(cost, sint, t)，C from (1, 0, 0) to (-1, 0, π)。计算C的线积分。
先来看C的轨迹，如果去掉z轴，那么C的参数化x = cost, y = sint正好是极坐标下的圆。现在加上了z轴，那么C的轨迹应当在柱面上。
示例2
找出b的值，使F = <y, x+byz,y2+1>是保守场；当F是保守场时，找出F的势函数。
验证：
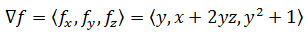
作者：我是8位的
出处：http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注公众号“我是8位的”
