多变量微积分笔记23——散度定理
散度定理，又称为高斯散度定理、高斯公式、高斯－奥斯特罗格拉德斯基公式或高－奥公式，是指在向量分析中，一个把向量场通过曲面的流动（即通量）与曲面内部的向量场的表现联系起来的定理。它经常应用于矢量分析中。矢量场的散度在体积D上的体积分等于矢量场在限定该体积的闭合曲面s上的面积分。
散度定理
散度定理是三维空间中的格林公式，大概是这样说的：如果S是一个封闭曲面，D是被曲面封闭的空间，n是指向D外侧的单位法向量，F = Pi + Qj + Rk是空间向量场，它在D上处处可微，则曲面S的通量等于散度在D上的体积积分：
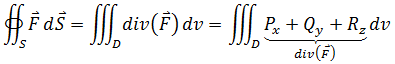
如果结合梯度，散度定理还有另一种写法：
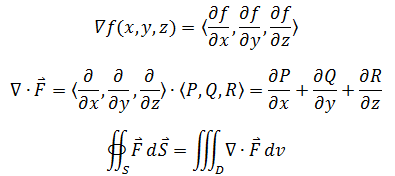
在介绍空间向量场中的通量时，看过这个示例：以a为半径的球面内，求向量场F = <0,0,z>的通量。
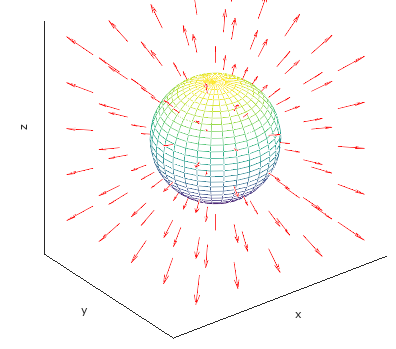
当时是用了球坐标系进行转换，最终得到结果是4πa3/3，现在可以使用散度定理直接计算：
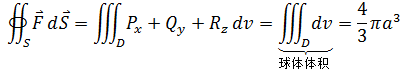
综合示例
示例1
如下图所示，求半径为r的半球，最在场F = yj中的半球球面的通量。
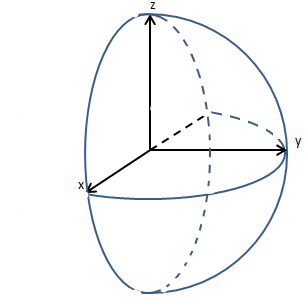
因为散度定理要求曲面闭合，所以这里不能直接使用散度定理。如果设球面是S1，半球在xz轴的切面是S2，由于S1和S2形成了闭合的曲面，所以：
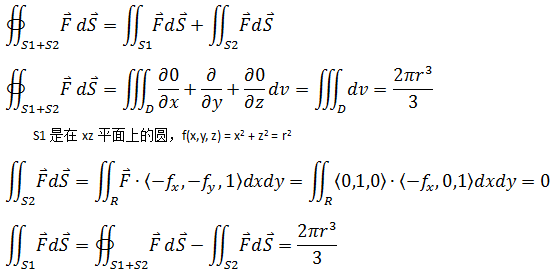
示例2
如下图所示，圆柱体轴心是z轴，底面中心点是原点，半径是R，高是h，求柱体在F = <x4y, -2x3y2, z2>中的通量。
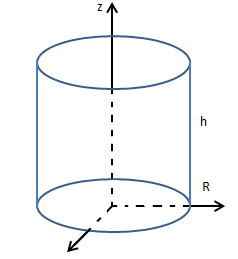
闭合曲面，直接套公式：
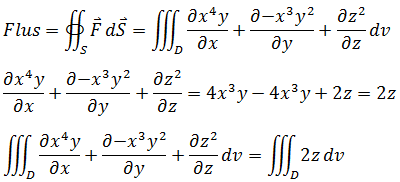
使用柱坐标转换：
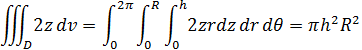
示例3
正方体在向量场F = <x,y,z>/ρ3中，ρ = (x2 + y2 + z2)1/2
a) 如果向量场中正方体中处处有定义，证明封闭曲面的通量是0；
b) 如果正方体的几个顶点是(±2, ±2, ±2)，能否根据a的结论认为正方体表面的通量是0？
a)
根据散度定理，如果闭合曲面在向量场中处处可微，则流过闭合曲面的通量等于散度在闭合曲面的体积积分：
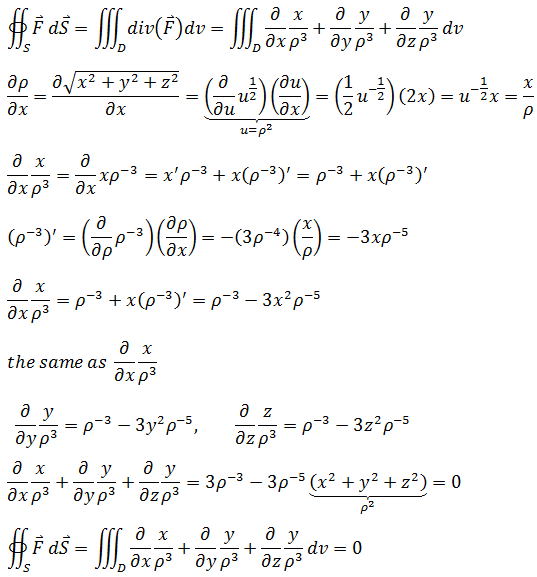
b)
答案是No，因为在0点处不可微，所以不能直接使用散度定理。
作者：我是8位的
