线性代数笔记7——再看行列式与矩阵
前面的文章已经对行列式和矩阵做了简单介绍,在经过向量与平面方程的铺垫后,让我们以新的视角去审视行列式与矩阵。
行列式
如果有两个向量<a1, a2>和<b1, b2>,那么这两个向量组成的行列式是:
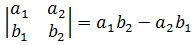
看起来只是表示一个简单的计算,仅仅计算了一个数值,但是别忘了,行列式是由向量组成的,它一定会表示向量间的某种关系。
在《线性代数笔记4——向量3(叉积)》中我们看到,二阶行列式表示了二维平面中以两个向量为临边的平行四边形的面积;三阶行列式表示在三维空间中以三个向量为临边的平行六面体的体积;推广到n维空间,n阶行列式表示在n维空间中图形的n维体积。实际上我们无法有效表示出三维以上的空间。对于物理世界中更多维的空间,绝大多数人都无法想象,但是数学却可以给出明确的定义。
对于n维空间的行列式,可以表示为:
Dn = |An×n|
其中A是一个n×n的矩阵。
行列式是由向量引出的,解释的也是向量的性质,在看到行列式时一定要在头脑中映射出向量,实际上线性代数的本质就是对向量的研究。
行列式的性质
性质1,如果Dn= |A|中某行的元素全为0,那么Dn = 0
这个性质较为明显,在多维空间中,行列式表示的是体积,如果其中一个维度的模为0,那么体积也是0。
性质2,如果Dn= |A|中某两行元素对应成比例,那么Dn = 0
很多时候我们都喜欢用实例推导性质,像下边这样:
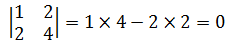
或者用代数形式:
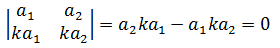
但是性质应当由定义推导,然后用计算去验证,而不是用计算去推导。现在我们尝试用行列式的定义去推导。行列式表示的是向量间的关系,以二维空间为例,如果某两行元素对应成比例,那么说明一种一个向量是另一个向量的延伸,它们的夹角是0°或180°,即二者平行,两个平行的向量围成的面积是0:
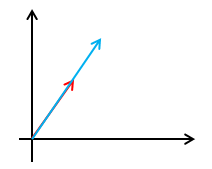
性质3,如果Dn= |A|中某两行元素互换,那么互换后的行列式变号,即|A|= -|A|
两个向量的模长是a和b,与x轴的夹角分别是α和β,如下图所示:
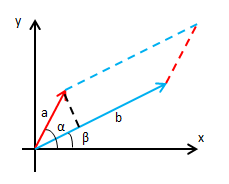
平行四边形的面积:
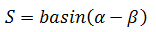
如果两个向量互换:
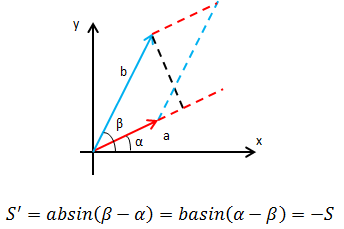
在代数学中,角度、面积、体积可以是负的。用计算去验证:
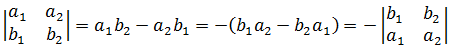
性质4,倍乘性质
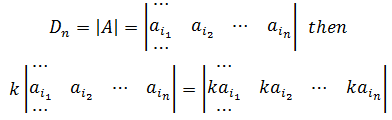
实际上是将外部的k乘到其中的一行,把平行四边形的一条边扩大k倍,则面积也扩大了k倍,如下图所示:
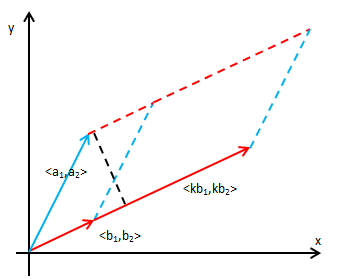
需要注意的是行列式与矩阵的区别,矩阵扩大k倍是将矩阵中的全部元素都乘以k(矩阵中的每个元素都对应了一个向量的分量,这在下文关于矩阵的介绍中会有所说明),这将有下面的关系:
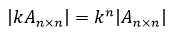
性质5,倍加性质
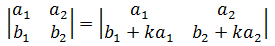
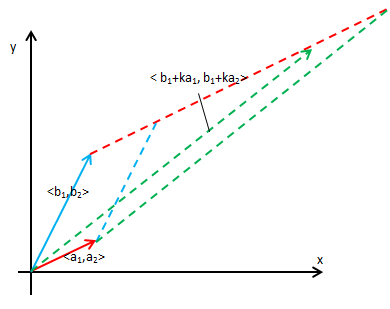
对于更高阶的行列式也一样。下图平行四边形的斜边展示了一个向量加上另一个向量的k倍:
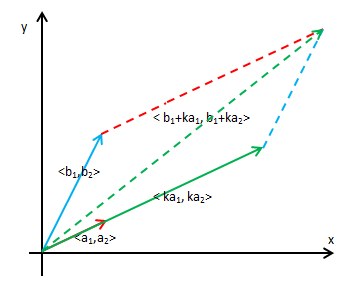
两个平行四边形的面积是相同的,所以倍加公式成立。
性质6,单行可拆(加)性
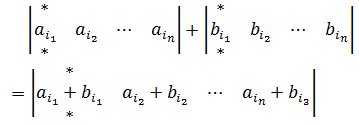
其中*号表元素完全相同,从左到右叫加,从右到左叫拆。以二阶行列式为例:
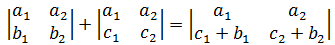
为了简单,将<b1,b2>和<a1,a2>分别设置在两个坐标轴上,如下图示:
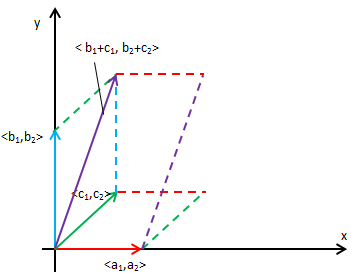
<a1,a2><b1,b2>所围平行四边形面积是a2 b2,<a1,a2><c1,c2>所围平行四边形面积是a2 c2,<a1,a2>< b1+c1, b2+c2>所围平行四边形面积是a2(b2+c2),由此可见性质6成立。
性质7,以上所有作用于行的性质也可以作用于列上,即|A| = |AT|
行列式的意义
行列式是由向量组成的,当Dn = |A| ≠ 0 时,意味着组成|A|的向量全部独立。所谓独立,就是向量围成的n维空间中图形的n维体积不为0。这似乎没有太大价值,但是如果把行列式转换为方程组就意义重大了,以二阶行列式为例:
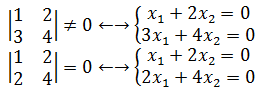
可以看到,对于全部独立的向量,方程组有唯一解,否则方程组无解或有无数解。当|A| ≠ 0时,说明至少有一个向量是“多余”的,正是这个多余的向量使得n维体积为0。以阶行列式为例,当体积为0时,说明三个向量在同一平面内,这意味着,一定可以通过倍乘和倍加性质用另外两个向量表示第三个向量,从而完全消除第三个向量。N元一次方程组需要N个完全不同的等式,现在少了一个等式,所以无法得到唯一解。
线性代数研究的是向量之间的关系,向量间最重要的关系就是独立或不独立,行列式是否等于0正是这种关系的有效描述。
行列式的计算
这里只介绍三阶行列式的计算,更多阶还是交给计算机吧。
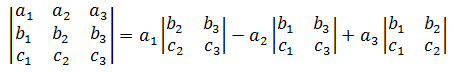
矩阵
矩阵在前几章已经有过介绍,这里需要强调的是,矩阵是由向量组成的。
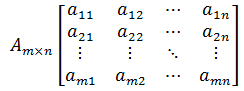
从列上看,A由n个m维列向量组成:
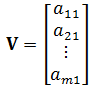
从行上看,A由m个n维行向量组成:
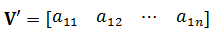
矩阵的秩
如果一个矩阵Am×n存在k阶子式不为0,且任意k+1阶子式全为0,称这个矩阵的秩是k,r(A)=k。
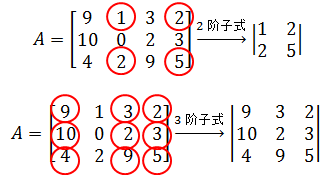
子式是行列式,如果A是一个3×4矩阵,它的一个2阶子式和一个3阶子式是:
这有什么用呢?
在行列式的意义中我们提到:向量间最重要的关系就是独立或不独立,行列式是否等于0正是这种关系的有效描述。由此看来,矩阵的秩r(A) = k表示矩阵中一定存在一个k阶行列式,这个行列式中的向量全部独立;且矩阵中对于任意k+1阶子式,都存在至少一个多余的向量。简言之,秩意味着矩阵中有且仅有k个独立向量。
行阶梯形矩阵
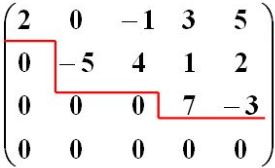
行阶梯矩阵是非零矩阵,它满足这样的性质:1)如果有0行,则0行种最下方;2)从行上看,从左边起,出现连续0的个数自上而下严格递增,如下所示:
若行阶梯矩阵还满足:1)台角位置元速为1;2)台角正上方元素全为0,则称该矩阵为行最简阶梯矩阵,如下所示:
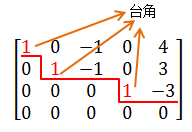
这有什么用呢?还是联系向量来看问题,在行阶梯矩阵中,阶梯数就是矩阵中独立向量的个数,也就是矩阵的秩;如果矩阵的秩是k,该矩阵一定能通过“初等变换”转化为阶梯矩阵,进而转化为行最简阶梯矩阵。
矩阵的初等变换
在经过变换后,矩阵表示的“数表”改变了,但是如果将矩阵看方程组,那么方程组的本质没有变,可以将初等变换看成方程组的消元过程。
变换1 ,互换变换

变换2,倍率变换
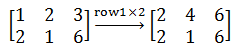
变换3,倍加变换
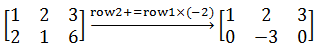
可逆矩阵与行最简阶梯矩阵
先给出结论,可逆矩阵一定能够通过若干次变换,转换成同阶单位矩阵,如下所示:
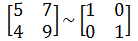
示例
将下列两个矩阵化为行最简阶梯矩阵:
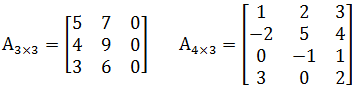
1) A3×3
首先计算矩阵的秩,A的最高阶子式是3阶。根据矩阵的性质:某行的元素全为0,那么Dn = 0;|A| = |AT|,所以D3=0。
现在取一个二阶子式:
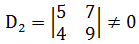
所以矩阵的秩r(A) = 2,这说明矩阵有2个独立向量,或者说矩阵中的第三个向量是多余的,因此矩阵可变换为:
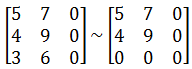
再来看D2,因为D2≠0,所以D2组成的矩阵可逆,也就是:
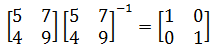
由此看来可逆的矩阵一定没有多余向量。既然方程组有唯一解,那么矩阵必然能够最终变换为右侧单位矩阵的形式,由此,A的行最简阶梯矩阵是:

2) A4×3
4×3矩阵,必然有矩阵的秩r(A) ≤ 3,说明行向量中一定有至少一个是多余的。由于行向量之间没有明显的倍数关系,所以我们将最右一行视为多余向量:
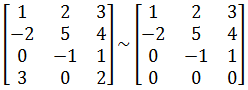
经过倍加变换:
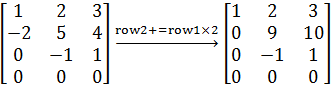
此时可以看出,<0,9,10>和<0,-1,1>围成的平行四边形面积不为0,<1,2,3>是空间向量,与前两者不在同一维度,所以:
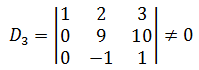
D3对应的矩阵有逆矩阵,并且可变换为同阶单位矩阵,所以:
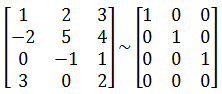
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号