多变量微积分笔记21——空间向量场中的通量
向量场 vector field（矢量场）是由一个向量对应另一个向量的函数。向量场广泛应用于物理学，尤其是电磁场。
建立坐标系(x,y,z)。空间中每一点(x0,y0,z0)都可以用由原点指向该点的向量表示。因此，如果空间在所有点对应一个唯一的向量(a,b,c)，那么时空中存在向量场F: (x0,y0,z0)→(a,b,c)
空间向量场
空间向量场与平面向量场类似，在空间中的每个点都有一个向量，它由三个分量PQR表示，这三个分量都是x,y,z的函数：
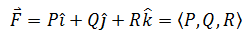
画出平面向量场已经很难，所以通常不要求画出空间向量场，但我们应当知道空间向量场中向量大致的朝向，是发散还是指向原点。空间向量场有着广泛的应用，比如万有引力场，空间中的流体场。
假设一个空间力场由一个指向原点的向量场给出，向量的大小与其到原点的距离的平方成反比，向量场如下图所示：
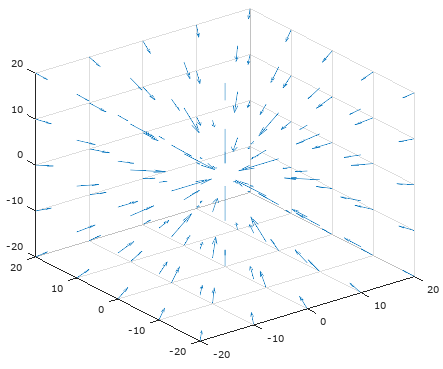
其中：
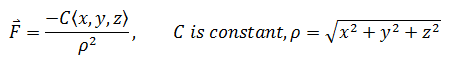
空间中的通量
在《多变量微积分笔记17——通量》介绍了平面向量场中的通量，它度量了单位时间内流体通过曲线的量；空间中的通量与之类似，只不过在三维空间内流体通过的是一个面而不是一条曲线，通量由流体通过的表面积来度量，所以要用面积分而不是线积分。
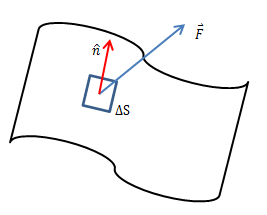
如上图所示，曲面处于三维空间的向量场F中，在每个点上都会产生不同的向量，通量就是F在法向量方向的分量。在平面的每一个点上，平面的法向量都有两个，这需要规定其中一个法向量的方向为正方向。对于面积小块ΔS来说，其通量就是单位时间内通过ΔS的流体的量：
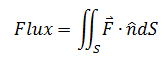
其中F·n就是F在单位法向量n方向的分量，之所以使用dS而不是dA代表面积积元，是因为我们习惯于把dA看成平面坐标中的面积。当向量与曲面相切时，通量为0，此时没有流体流过曲面。
在平面的通量中，用dy,-dx来化简nds：
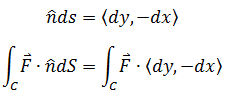
在空间中，用向量dS化简ndS，使向量dS与曲面垂直，其模长与面积积元有关：
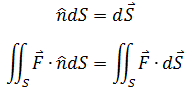
面积分
球面积分
在以a为半径的球面内，求向量场F = <x,y,z>的通量。
F是从原点向外散射的，所以球面的法向量与F平行，根据公式：
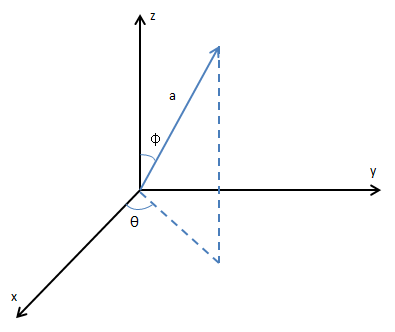
现在需要找到正确的α，使得n变成单位法向量。来看球的xy剖面图：
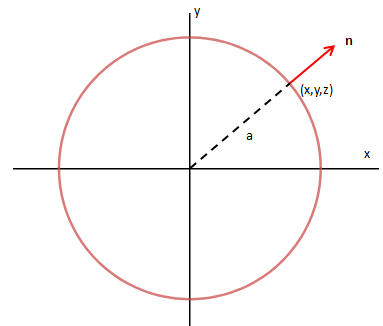
由上图可见：
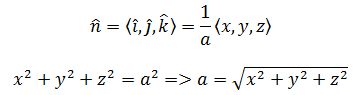
现在，在球面上，F在单位法向量n方向的分量：
也可以以点积的方式计算：
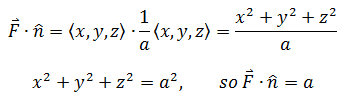
最终：
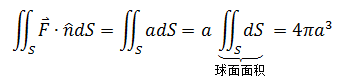
仍然是同样的球体，现在向量场变成了 H = <0,0,z>，重新计算通量：
问题转换为如何求解二重积分，这就需要知道dS是什么以及如何将dS和z参数化。在《多变量微积分笔记20——球坐标系》中介绍了球坐标，现在我们可以用球坐标化替换x,y,z：
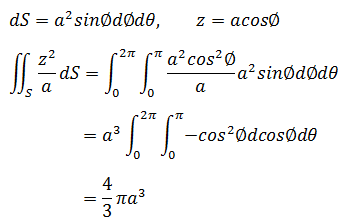
需要注意的是，由于这里计算的是面积分且dS并不在xy平面，所以无法用dxdy代替dS；但有时候，根据场景的不同，可以用dxdy代替dS，比如求水平面z = a在场中的通量。这里的关键就是明确dS究竟是什么，如果平面平行于yz轴，那么dS = dydz。
总结一下，如果在向量场中存在一个以原点为球心，以a为半径的球，那么：
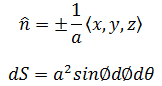
n的正负号取决于单位法向量的方向。
柱面积分
现在来看看柱体的面积分。下图是轴心在z轴，半径为a的柱体：
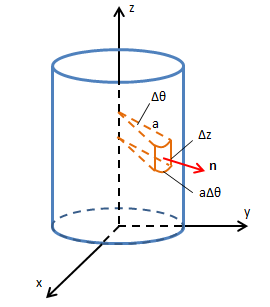
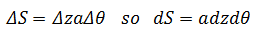
n与xy平面平行，所以n在z方向上的分量是0，因此：
综合示例
示例1
a) 计算空间向量场F = <0, 0, 1>中，x2 + y2 = 1的通量。
b) 计算空间向量场F = <0, 1, 0>中，在xz平面的单位正方形的通量。
a)
很明显x2 + y2 = 1是一个以z轴为轴心的无限柱体；向量场中的所有向量都与xy平面垂直，没有xy方向的分量，所以 x2 + y2 = 1的通量是0。
如果计算的话：
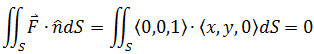
b)
向量场中的所有向量都垂直于xz平面，也就是与正方形的法向量方向相同，所以：
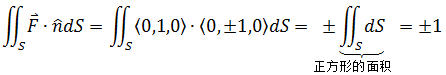
示例2
如下图所示，求在向量场F =<z,x,y>中1/4柱面向外的通量。
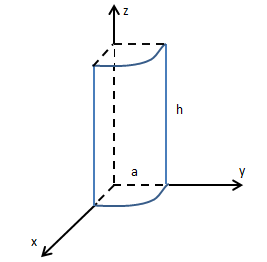
从柱面很自然联想到柱坐标系，在柱坐标系中：
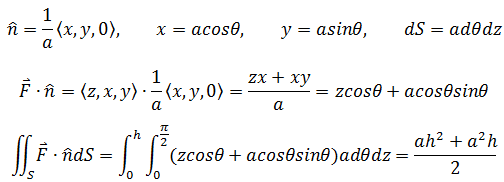
示例3
如下图所示，求在向量场F =<xz,yz,z2>中半径为a的1/4球体在第一象限向外的通量。
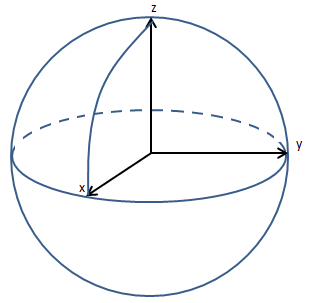
在球坐标系中：
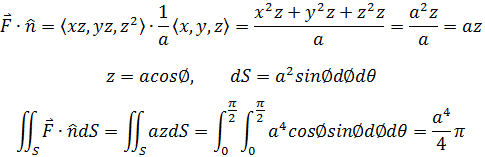
作者：我是8位的
