多变量微积分笔记20——球坐标系
球坐标系是三维坐标系的一种，用以确定三维空间中点、线、面以及体的位置，它以坐标原点为参考点，由方位角、仰角和距离构成。球坐标系在地理学、天文学中都有着广泛应用。
球坐标系
球坐标中是这样表示空间中一点的：用ρ表示点到原点的距离，0 ≤ ρ≤ +∞；在ρz平面上，从z轴正半轴向ρ偏转的角度是φ，0 ≤ φ≤ π；从x轴偏转到平面的角度是θ，0 ≤ θ≤ 2π，如下图所示：
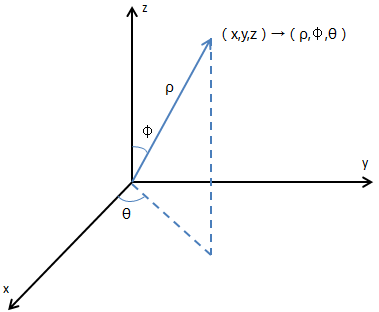
被称作球坐标的原因是，如果固定了ρ=a作为半径，通过移动ρ就可以得到一个球面，φ就是ρ的南北朝向，0°≤ φ < 90°，ρ朝北，90°<φ≤ 180°，ρ朝南：
如果将上图看作地球，φ和纬度相似，都是衡量点到南北极点的距离。当然，在具体度量上有所差别，地理上赤道是0°纬线，然后向两极递增；球坐标的φ从北极点出发，向南极递增，赤道位置是90°。θ和经度类似，用来衡量东西方位，因此可将x轴正半轴的指向看作本初子午线，也就是0°经线，由于球坐标中θ的取值是[0, 2π],所以只有东经没有西经。
也可以通过柱坐标来理解球坐标（关于柱坐标，可参考《多变量微积分笔记19——直角坐标系和柱坐标系下的三重积分》）：
球坐标到柱坐标的互相转换相当于rz平面的极坐标表示法：
以上是球坐标系的所有公式，实际上只要记住图形就可以了。
如果仅定义了ρ和φ，相当于向量绕着z轴旋转；特别地，当ρ从原点出发绕z轴旋转，将形成一个圆椎体，如下图所示：
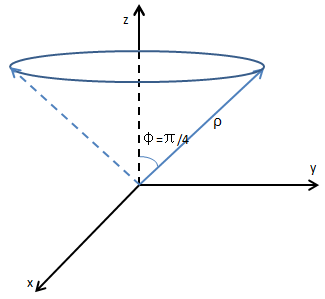
如果φ=π/2，则变成扁平的高度为0的圆锥——xy平面的圆。
球坐标系的积分
想要计算三重积分，就需要知道体积积元dv，在球坐标系中dv需要转换成dρdφdθ，那么三者的顺序，也就是面积积元应当是什么？
尝试用dφdθ作为面积积元，如下图所示：
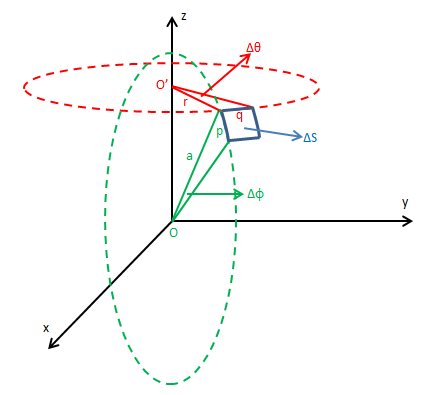
ΔS是三维空间中物体便面积的微小面积块，在球坐标系中，当Δφ和Δθ足够小时，ΔS的两边p和q可以看作以O和O’ 为圆心的圆的微小弧长，两个圆互相垂直。如果两个圆的半径分别为r和a，则：
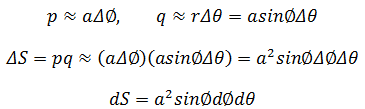
Δρ是ΔV的厚度积元，对于球坐标来说，a = ρ：
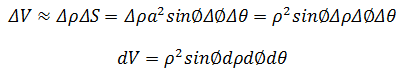
通常按照dρdφdθ的顺序计算最为简单。
综合示例
示例1
计算单位球和z = 2-1/2所围的区域的体积：
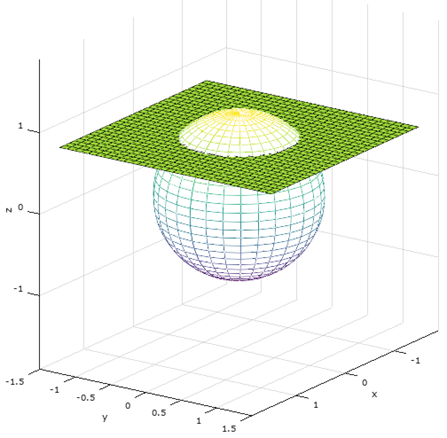
尝试使用球坐标处理，积分很简单：
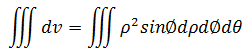
问题转换成确定ρφθ的取值范围。因为是球体，很明显θ的取值范围就是[0, 2π]。通过球体的切面图形确定其余两个积元的取值：
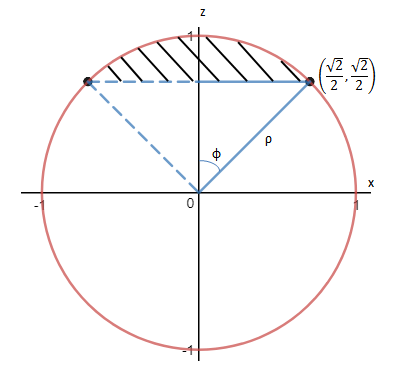
切面左右两侧对称，只需要观察一侧即可。φ是直角三角形的一角，随着ρ的滑动，φ的取值将是[0, π/4]。无论φ怎样取值，ρ的最大值都在球面上，所以ρ的最大值是1。当φ=0时，ρ在z轴上，此时ρ的最小值是2-1/2。这里很容易将ρ的取值误判为[2-1/2, 1]，这需要用下图解释：
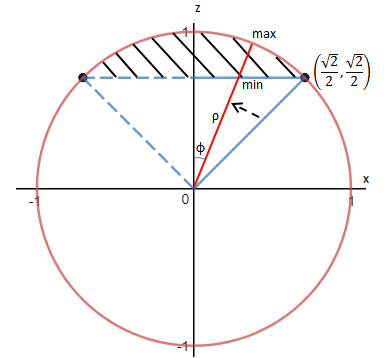
ρ向z轴方向旋转，此时φ减小，ρ的最大值始终位于球面，最小值是ρ与平面的交点处，所以ρ与φ有关。当ρ取最小值时，z始终是2-1/2，通过球坐标的公式可知：
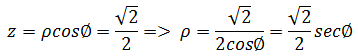
最终：
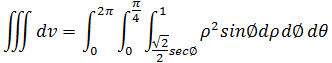
分步计算（三角函数的积分可参考《数学笔记21——三角替换2（tan和sec）》）：
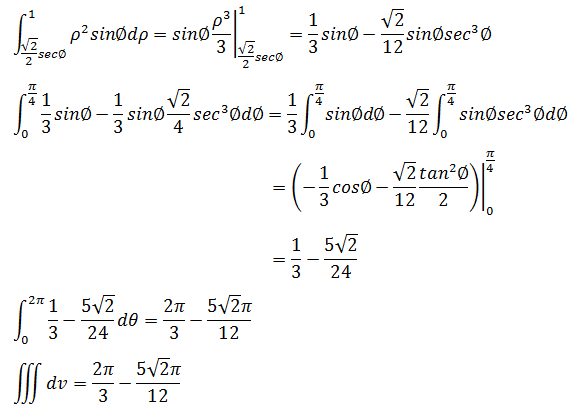
示例2
立体区域D是圆心在(0, 0 , 1)的单位圆的上半球，计算D的体积和圆点到D的平均距离。
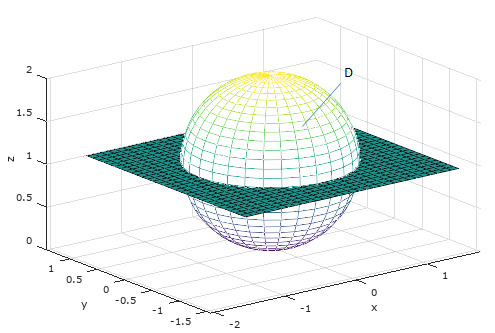
根据球的图体积公式：
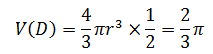
现在使用积分去计算。和示例1一样，很容易确定θ的积分域是[0, 2π]。通过zx轴的截面确定φ的积分域：
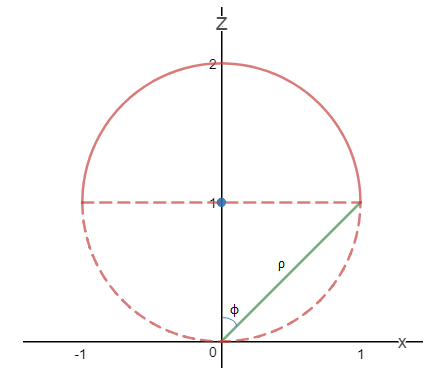
上图可以看出，φ的最大值是π/4，φ的积分域是[0, π/4]。ρ的取值如下图所示：
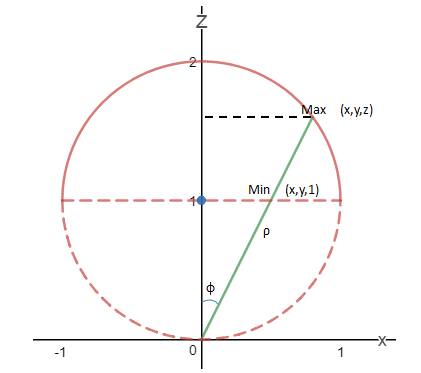
可以看到，ρ的积分上下限都不固定，它们随着φ的变换而改变，Max点是(x,y,z)，其中：
现在的问题是如何求得ρ的积分上限？求解方式是从几个已知条件和极坐标的公式中让ρ变成θ和φ的函数：
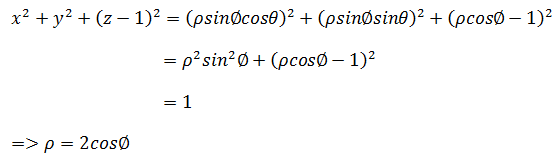
最终：
又是一个冗长的三角换元，分步计算如下：
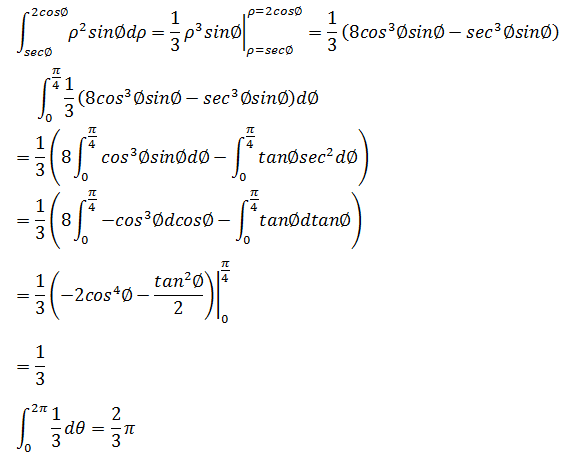
球的体积也可以使用一元积分的圆盘法球的，可参考《数学笔记17——定积分的应用2（体积）》。
在《多变量微积分笔记10——二重积分的应用》中介绍过均值问题，三重积分与之类似，距离的均值相当于在D区域内对ρ进行积分处理：
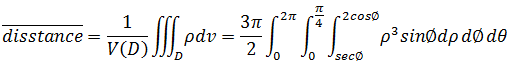
作者：我是8位的
