概率笔记4——重要公式
概率公式是概率计算中的重要环节,全概率公式、贝叶斯公式等可以运用于复杂事件的概率, 而所有这些公式又是由基本公式推导出来的。
基本公式
对于任意事件A和B
公式1说的是A发生的概率等于1减去A不发生的概率(对立事件的概率)。换种说法可能更好理解,A发生的概率加上A不发生的概率等于1,也就是A事件要么发生要么不发生。这是废话,也是很重要的实话,因为很多时候直接计算A发生的概率很困难,但计算A不发生的概率确很简单。
公式2说的是当A发生且B不发生的概率;公式3是当且仅当A,B中至少有一个发生的概率;公式4不解释。2、3和集合运算一致,公式3还有两个等同写法:

值得注意的是,不能像下面这样写:
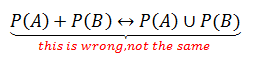
A和B是事件,事件是集合,所以可以使用集合符号,但P(A)和P(B)是概率,是具体的数值,所以不能使用集合符号。
互斥事件
如果有两个事件A和B,发生了A就不会发生B,发生了B就不会发生A,那么他们两个是互斥的,如果用集合表示,则A∩B = φ。互斥事件也叫互不相容事件。
对于互斥事件A和B:
这实际上来自基本公式:
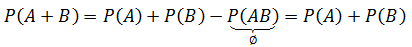
对于更多的互斥事件,如果A1,A2,A3…An两两互斥,则当且仅当A1~ An中至少有一个发生的概率:
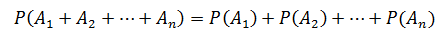
上式更专业的写法:
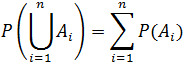
独立事件
什么是独立
两个事件是独立的,直觉上是指:在一次实验中,一个事件的发生不会影响到另一事件发生的概率,二者没有任何关系。如,骰子掷出“6点”的事件和骰子掷出“1点”的事件是相互独立的。
需要注意的是,“互斥”是描述的是集合关系,“独立”描述是概率关系,二者间不在同一维度,不要试图将二者联系到一起。
独立事件有一个充要条件:如果n个事件互相独立,那么如果它们中的任意一部分换成各自的对立事件后,所得的新n个事件互相独立:
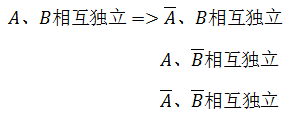
公式
对于独立事件A和B,二者同时发生的概率等于二者的乘积:
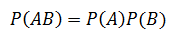
其等同写法:
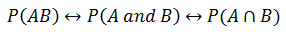
注意,只有在A和B是独立事件时上式才成立。
推广到更多独立事件,如果A1,A2,A3…An相互独立,则A1~ An同时发生的概率:
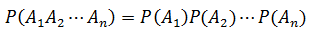
更专业的写法:
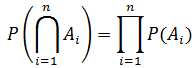
如果A1,A2,A3…An相互独立,则当且仅当A1~ An中至少有一个发生的概率:

条件概率
垂帘听政
条件概率是指在A事件发生的条件下,事件B发生的概率,用符号表示:
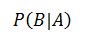
中间的竖线看成帘子,A是太后,B是幼主,A对B垂帘听政。
公式
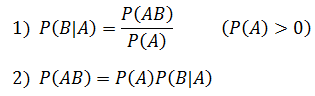
实际上两个公式是一样的,将公式1左右两侧同时乘以P(A)就得到了公式2。
需要注意的是,这里并没有指明A和B是独立事件。如果A和B是独立事件,根据独立事件公式,P(AB) = P(A)P(B),最后一项由P(B|A)变成了P(B),意思是B的发生与A无关,即太后想要垂帘听政,但是幼主长大了,不听她的。
注意,虽然P(AB) = P(BA),但P(A|B)≠P(B|A):

对于更多事件,可以反复使用公式1和2:
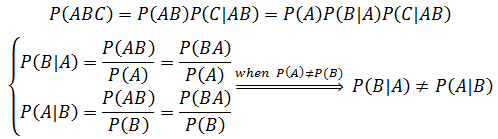
全概率公式
引例
一个村子里有三个独立作案的小偷,小偷参与盗窃的概率和盗窃能力已知,每次盗窃事件仅与其中一人有关,求村子失窃的概率。
有点难度了。
首先需要将问题转换成数学模型。令B事件为村子失窃事件,所求的是P(B);设三个小偷A1,A2,A3,小偷的全集就是 Ω = { A1∪A2∪A3};每次盗窃事件仅与其中一人有关,A1,A2,A3是互斥的;小偷盗窃能力相当于该小偷在实施偷盗的情况下失窃的概率,P(B|Ai)。现在:

最终得到的就是全概率公式了,实际上就是由简单概率一步步推导而来,最重要的还是建立正确的概率模型。
公式
如果事件A1、A2、A3…An 构成一个完备事件组,即它们两两互不相容,其和为全集Ω;并且P(Ai) > 0,则对任一试验B有:
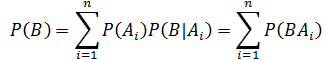
右侧的两个表达式之所以相等,是因为:
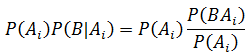
不同的马甲
全概率公式的马甲众多,下面是教科书中的一个示例。
电子厂所用原件是由三个厂家提供的,已知以下数据:
|
原件场 |
次品率 |
供货份额 |
|
1 |
0.02 |
0.15 |
|
2 |
0.01 |
0.80 |
|
3 |
0.03 |
0.05 |
原件在仓库混合存放,每个元件没有明显区别,从仓库中随机取一个,次品的概率是多少?
数学模型:A1,A2,A3分别表示元件是由三家元件场生产的,Ω = { A1∪A2∪A3};从仓库中随机取一个,得到次品的事件是B,P(B)为所求;P(Ai)是供货份额,P(B|Ai)是Ai的次品率。
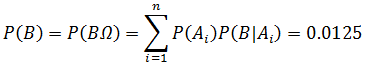
贝叶斯公式
公式
大名鼎鼎的公式,常见的一个版本:
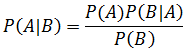
很多时候,求P(A|B)很困难,但求P(B|A)却很容易。上面的公式实际上是条件概率公式简单的推导:
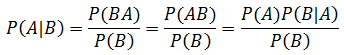
结合全概率公式:
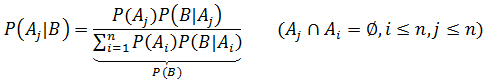
示例
对于上一节的元件次品问题,从仓库中随机取一个,如果是次品,那么该次品是哪个厂商的概率最大?
数学模型:A1,A2,A3分别表示原件是由三家元件场生产的,从仓库中随机取一个,得到次品的事件是B,P(Ai|B)就表示次品是Ai生产的概率。

先下手为强
最后来看一个示例,甲乙二人轮流独立地对同一目标射击,谁先命中谁获胜,甲命中的概率是α,乙是β。现在由甲先射击,求二人获胜的概率分别是多少?
甲获胜的全集:{第1次射击时获胜∪第3次射击时获胜…∪第2n-1次射击时获胜},n是自然数,n ≥ 1;甲第3次射击获胜的前提是,甲第1次射击失败且乙第2次射击失败,以此类推,甲的获胜全事件Ω = {甲第1次射击获胜∪(甲第1次射击失败∩乙第2次射击失败∩甲第3次射击获胜)…∪(甲第2n-1次射击时获胜(甲之前都失败∩乙之前都失败))}。用A、B分别表示甲乙的获胜事件,各事件之间相互独立(轮流独立射击),获胜事件之间互斥(谁先命中谁获胜,只能有一人胜出),下标表示二人出场次数,则:

幂级数可参考《数学笔记31——幂级数和泰勒级数》
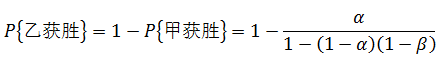
如果甲乙实力相当,α = β = p < 1,q = 1-p < 1 则:

所以说二人势均力敌时,先下手者为强。该结论也出现在其它运动中,比如围棋,先手需要胜出后手5个棋子才算获胜,而后手只需要胜出一个棋子就算获胜。
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号