ML(附录1)——梯度下降
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。
简单地说,梯度下降就是沿着沿梯度下降的方向求解极小值时的自变量。
关于梯度的知识可参考《多变量微积分5——梯度与方向导数》
梯度下降的原理
二元函数w(x,y) = (x – 10)2 + (y – 10)2,其梯度:
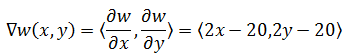
如果在w上选取一点(xn, yn),w沿着梯度下降方向,在x方向上的变化率:
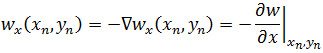
自变量x沿着梯度下降方向的变化:
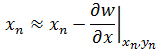
反复迭代,在达到临界点时,就可求得w在极小值时的x;同理可求得在极小值时的y。
问题是这样做实在太慢,迭代过程及其耗时,所以人们在此基础上设计出更加快速的处理办法——舍弃精确值,求得可接受的近似值。
学习率
实际应用中,梯度下降法增加了“学习率”的概念:
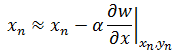
上式中的α就是学习率,也称为“步长”。梯度下降算法每次迭代,都会受到学习速率α的影响。偏导指明了变化的方向,而学习率则指明变化的步伐,实际上每次迭代一下,就可以更换一个新的α,只是为了方便才用一个。
本节剩余内容摘自 https://blog.csdn.net/chenguolinblog/article/details/52138510
如果α较小,则达到收敛所需要迭代的次数就会非常高;如果α较大,则每次迭代可能不会减小代价函数的结果,甚至会超过局部最小值导致无法收敛。如下图所示情况:
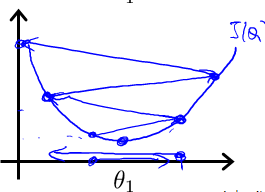
根据经验,可以从以下几个数值开始试验α的值,0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …
α初始值位0.001, 不符合预期乘以3倍用0.003代替,不符合预期再用0.01替代,如此循环直至找到最合适的α,然后对于这些不同的 α 值,绘制 J(θ)随迭代步数变化的曲线,然后选择看上去使得 J(θ)快速下降的一个α值。观察下图,可以发现这2种情况下代价函数 J(θ)的迭代都不是正确的:
根据经验,可以从以下几个数值开始试验α的值,0.001 ,0.003, 0.01, 0.03, 0.1, 0.3, 1, …
α初始值位0.001, 不符合预期乘以3倍用0.003代替,不符合预期再用0.01替代,如此循环直至找到最合适的α,然后对于这些不同的 α 值,绘制 J(θ)随迭代步数变化的曲线,然后选择看上去使得 J(θ)快速下降的一个α值。观察下图,可以发现这2种情况下代价函数 J(θ)的迭代都不是正确的:
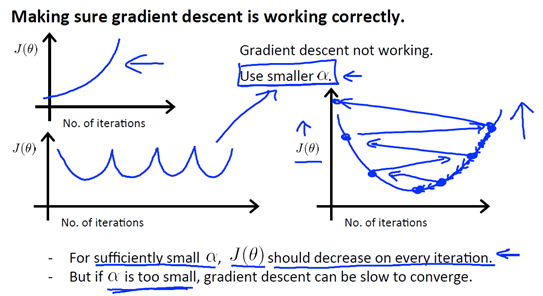
第一幅图,曲线在上升,明显J(θ)的值变得越来越大,说明应该选择较小的α
第二幅图,J(θ)的曲线,先下降,然后上升,接着又下降,然后又上升,如此往复。通常解决这个问题,还是选取较小的α。
在机器学习中的应用
如果机器学习算法的假设函数(hypothesis function) hθ(x)如下:
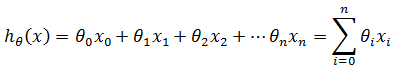
hθ(x) 是线性回归模型,设x0= 1,θ是权重,每个训练样本有n个特征,即训练样本是n维数据。对于初始权重,可全部设为一个常数。
对于给定的训练集,目标是找到最佳的hθ(x)以拟合最多数据,此时损失函数J(θ),也就是机器学习策略函数达到最小。如果全部预测正确,则对于所有训练数据都有hθ(x) – y =0
如果用平方和定义J(θ),则:
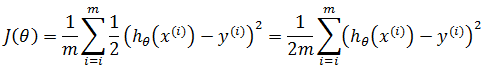
上式表示共有m训练样本,y表示实际结果,上标表示第i个训练样本,hθ(x(i)) - y(i) 表示在训练集的第i个样本中,预测结果与实际结果的差值。前面加上1/2是为了在求导时使J(θ)简化,在后续推导中可以看到。
假设m = 1,即仅有一个训练样本,此时:
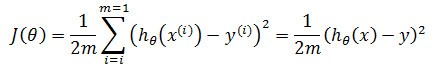
目标是使J(θ)达到最小,由于x和y已知,此时的 θ 值即为所求参数,根据梯度下降法:
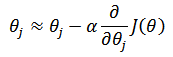
当i = 1时,第一个权重:
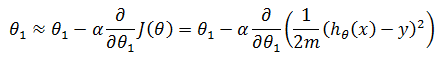
根据链式求导法则计算偏导(可参考《多变量微积分》的相关章节):
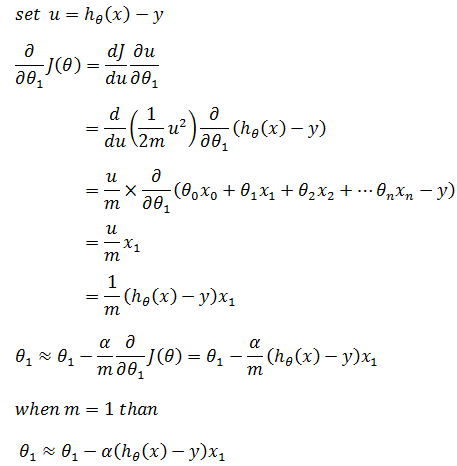
推广至m个训练样本,对于任意θ,梯度下降迭代表达式为:
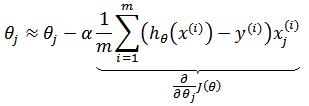
如果令θ是n维向量,可将上式化简:

如果用矩阵表示,梯度下降可以更加简洁:

当梯度下降到一定数值后,每次迭代的变化很小,这时可以设定一个阈值,只要变化小于该阈值,就停止迭代,而得到的结果也近似于最优解。需要注意的是,在新一轮迭代时,因为θ已经得到了更新,所以将使用新的hθ
以二元特征为例,下面是正确做法和错误做法的对比:
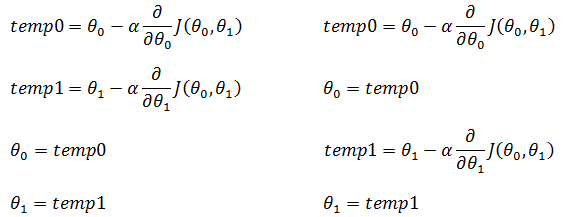
批量梯度下降法
上面对于权重的推导过程就是批量梯度下降法,每一次迭代都要遍历所有训练样本,不适用于训练样本数量极多的情况,于是提出了随机梯度下降。
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
随机梯度下降法
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是每次仅仅选取第 i 个随机样本来求梯度:
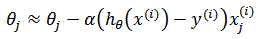
i 不是定值,在每次迭代时都重新选取。随机梯度下降法速度比批量梯度下降快了很多。随机梯度下降的每次迭代,有可能变大或变小,但总体趋势接近全局最优解,通常参数值会十分接近最小值。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
小批量梯度下降法
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于m个样本,我们采用其中的k个来迭代,1<k<m。一般可以取x=10,当然根据样本的数据,可以调整k的值:
优点:两种算法的折中;
缺点:两种算法的折中。
如果样本量比较小,采用批量梯度下降算法。如果样本太大,或者在线算法,使用随机梯度下降算法。在一般情况下,采用小批量梯度下降算法。
与最小二乘法的比较
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。最小二乘法可参考《多变量微积分笔记2——最小二乘法》。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”





 浙公网安备 33010602011771号
浙公网安备 33010602011771号