多变量微积分笔记11——变量替换
在二重积分中,极坐标替换是一种特殊情况,更一般的变量替换后的面积元是通过雅可比行列式来关联,替换后的积分域也会随之变动。
变量替换
二重积分可以计算面积,现在有一个椭圆 (x/a)2 + (y/b)2 = 1,如何计算该椭圆的面积?
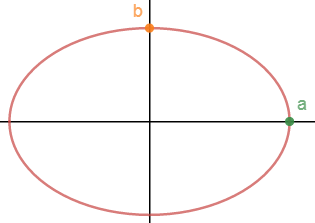
很容易写出Area = ∫∫Rdxdy,积分区域是(x/a)2 + (y/b)2 = 1,现在的问题是如何计算的内外积分的积分域?这当然可以通过代数法转换,将x写作y的表达式,但这个复杂的表达式多少会有些尴尬。椭圆也不能轻松地转换为极坐标,因为r的上限也是变化的。
现在尝试一种新的方案,如果令u = x/a, v = y/b,则椭圆将转换为 u2 + v2 = 1,退化成圆。对u和v计算微分:

变量替换的主要目的是简化被积函数或积分域,从而更容易地求得积分。
变量的变化率
上面方法将原变量表达式转化为一个新的简单变量,从而求得结果,其中最重要的步骤是求得dxdy和dudv之间的关系,那么对于更复杂的情况,这种方法还能否适用?
假设出于某种目的,我们做了这样的变换:u = 3x – 2y,v = x + y。现在dA是xy坐标系的面积积元,dA = dxdy;dA’ 是uv坐标的面积积元,dA’ = dudv。二重积分的思想是ΔA的面积乘以ΔA的函数值从而得到小柱体,再把这些小柱体相加,但是变换成uv坐标后,ΔA’的面积并不等于ΔA的面积:
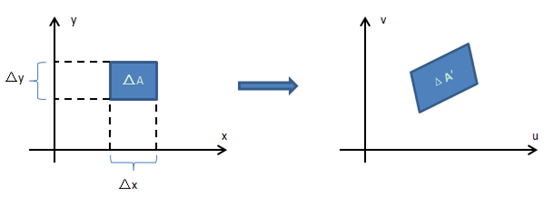
ΔA≠ΔA’
这实际上是线性变换,用一个简单的方法说明,让ΔA是小正方形,Δx = Δy = 1,变换后将得到一个平行四边形:
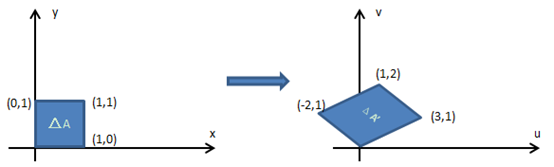
可以利用叉积求得ΔA’ 的面积:

由此可见,ΔA’ = 5ΔA。
值得注意的是,如果将Δx和Δy代入u和v,得到Δu = 3Δx – 2Δy,Δv = Δx + Δy,由于变换后的图形并不是正方形,所以ΔA’ ≠ ΔuΔv,ΔA’ 是平行四边形两条边的向量的叉乘:
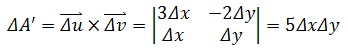
至此,我们确定了dxdy和dudv之间的关系:
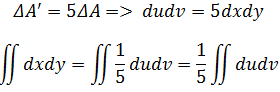
雅可比行列式
如果二元积分的被积函数f(x,y)中的变量被替换为u = u(x, y),v = v(x, y),那么u和v的微小改变,是轻轻扰动x和y的综合结果:

如果用矩阵表示:
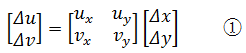
这实际上说明,对于线性变换,小矩形将转换为平行四边形,面积的放缩比例就是偏导的行列式。如果A = ΔxΔy是一个顶点在原点的矩形:
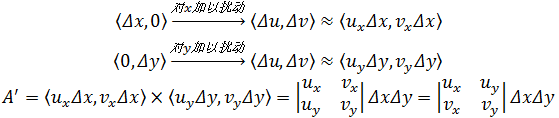
由于这个行列式的结果和转置后结果一致,所以放缩的倍数就是之①的矩阵行列式。这个行列式被称为雅可比行列式,用数学符号表示:
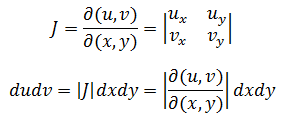
雅可比行列式描述了从xy坐标到uv坐标后,面积积元的变换比率。需要注意的是,雅可比行列式需要加上绝对值,因为行列式可能出现负值,但面积一定是正的。
用雅可比式验证极坐标
在《多变量微积分9——极坐标的二重积分》中提到过,从xy坐标转换到极坐标后,面积积元的变换率是 dxdy = rdrdθ:
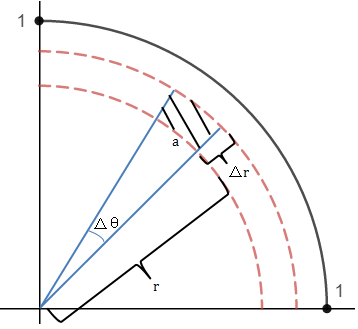
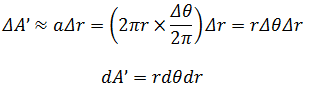
用雅可比式转换,注意此处是用x和y替换r和θ:
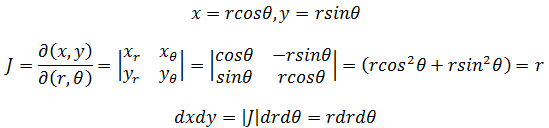
这再一次说明数学是可以互相佐证的,高级理论可以证明低级理论,低级理论又可以为高级理论的提供推导步骤。
变量替换后的积分域
用变量替换计算下面的积分:
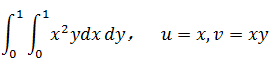
如果不使用变量替换,直接计算结果:

在试用变量替换时,首先使用雅可比式计算dudv和dydx之间的比率,然后转换被积函数:
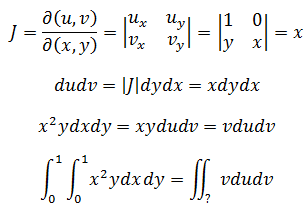
现在的主要问题是转换后的积分域。先来看xy坐标系,由于积分域0 < x < 1,0 < y < 1,所以积分的范围就是一个正方形:
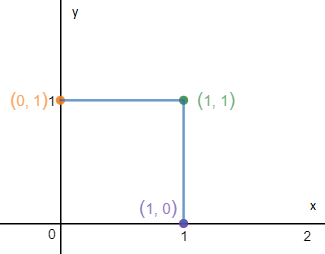
现在需要找出u和v是如何变化的。
在原坐标系计算积分域
可以这样思考,对于∫∫vdudx,先计算内积分,也就是先对u积分,把v看作常量,u看作变量,也就是把v = xy看作常量,u = x看作变量。把v = xy看作常量,意味着xy = C是一个双曲线:

如果v的值固定,那么v就是双曲线上的一点。对于不同的v,能取到不同的双曲线:
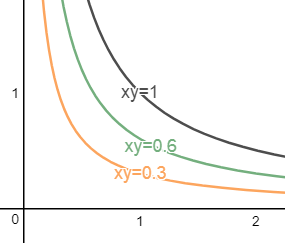
把双曲线加入到正方形中:
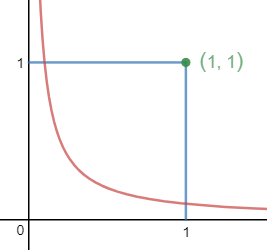
现在u = x是变量,v = xy是常量,这意味着当x变化时,就是在其中一条双曲线上移动。对于∫∫vdudx,我们首先回答的问题是当v固定时,u是积分域是什么?
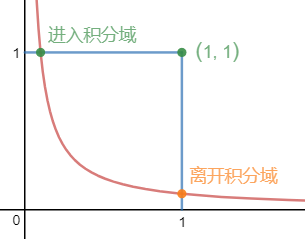
如上图所示,在离开积分域时,u = x = 1;在进入积分域时y = 1,所以:
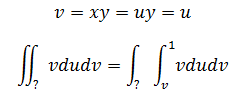
现在完成了内积分。对于外积分来说,就是在正方形区域内双曲线族所能达到的最大值和最小值:

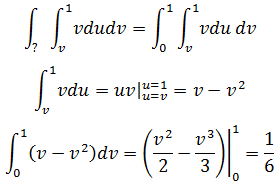
通过坐标变换计算积分域
还可以通过坐标系变换的方式计算积分域。xy坐标系在转换成uv坐标系时,有4条边需要解释:

x = 0和x = 1转换后:

y = 1,转换后,v = xy = x = u;y = 0,转换后v = 0:
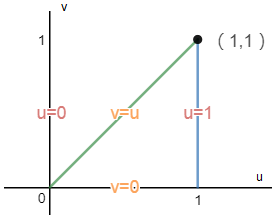
转换后的积分域就是三角形围成的面积。
如果以u为外积分,v为内积分,可以确定0 < u <1,v的取值如下图所示:
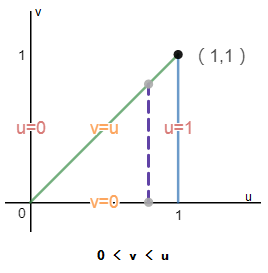
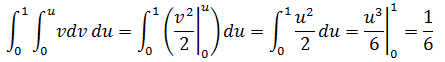
可以看到,转换前后的计算结果相同。
综合示例
示例1
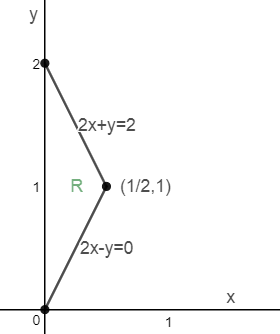
用变量替换计算积分∫∫R(4x2 – y2)4dxdy,u = 2x – y,v = 2x + y,R区域如下图所示:
雅可比行列式:
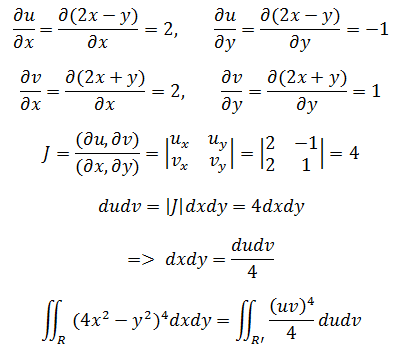
为了计算R’,尝试将xy坐标系转换为uv坐标系,只需要对边和点进行解释:

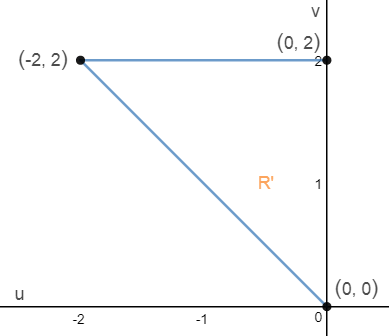
对比两个三角形,R的面积R = 1/2(2 * 1/2) = 1/2;R’的面积R’= 1/2(2 * 2) = 2;R’ = 4R,坐标转换后面积放大了4倍,这也验证了雅可比表达式,dudv = 4dxdr 。
三角形的斜边是u = -v,现在可以很容易得出转换后的积分域:

示例2
计算变量替换后的积分域。
∫∫R1/x2dxdy变量替换u = x2 – y2,v = y/x,xy坐标系的R区域中第一象限,在y=1/x下方,x2 – y2=1上方,如下图所示:
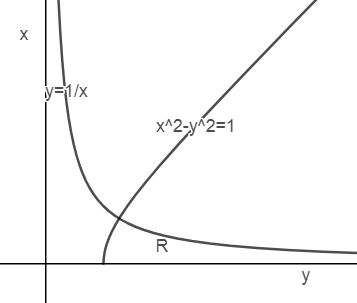
转换坐标系后,u = x2 – y2 = 1:

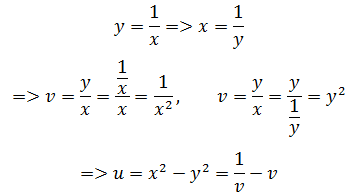
坐标系转移后:
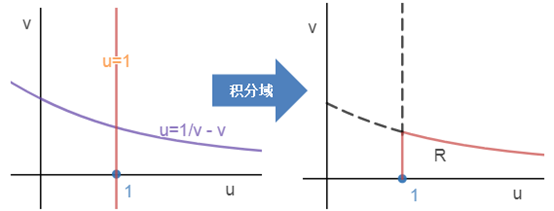
设两条曲线的交点是(1,a),可知积分域:
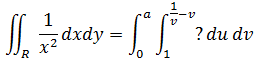
雅可比行列式:
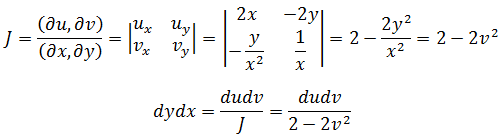
现在需要用uv代替1/x2:
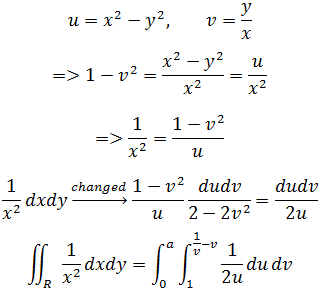
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号