多变量微积分笔记10——二重积分的应用
二重积分的几何意义是计算物体的体积，但是在实际问题中，二重积分还可以用来计算面积和均值。
计算面积
计算面积容易联想到单变量积分的几何意义，但通常这是用二重积分来完成的。
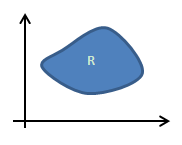
给出一个平面上的区域R，求R的面积。如果使用一元积分计算，会发现这并不容易，因为一元积分的几何意义是曲线与x轴围成的面积，而现在是要计算闭合曲线围成的面积。此时二元积分会比较有用。
将R区域的面积分成无数个小块，每个小块的面积都是dA，R的面积也就是dA之和（可参考《多变量微积分8——二重积分》）。如果用二重积分表示，R区域的面积就是函数f(x,y) = 1在R上的二重积分：
如果按照体积去思考，上式就是函数f(x,y) = 1的图形下的体积。由于在三维坐标中，f(x,y) = 1的图像是高度为1的水平面，所以二重积分表示底面积是AreaR，高度为1的棱柱的体积；体积等于底面积AreaR乘以高，高度是1，所以体积等于底面积。
通常我们不按照体积去思考，而是直接把∫∫RdA看成R区域的面积微元dA的总和。
考虑一个均匀的平面物理物体，比如一个金属板，它的质量就可以用二重积分计算。平面金属板的质量是板上每一小片质量的总和。一个平面物体的密度是每单位面积元的质量，因此可以对密度积分求平面物体质量。用Δm表示质量，ρ表示密度，ΔA表示小块区域，则：
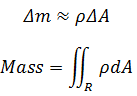
需要注意的是，二重积分只能处理平面，上式表示对密度做积分得到平面物体的质量。如果要计算空间物体的质量，就必须计算体积，这是三重积分的工作。
计算平均值
二重积分的另一个应用是求区域上数量的平均值，即在区域R上求函数f的平均值。
我们知道在有限数据集上求平均值的方法——用数值总量除以数值个数，比如计算一个班级学生的平均身高。如果是无限数据集的平均值呢？比如测量一个房间的平均温度，我们通常的做法是选取一些点去测量，然后计算这些点的平均值，结果的真实度取决于测量点的个数。理论上有无限多个点，所以这种方式无法表述真正的数值。
实际上，数学上定义连续平均值的方法是对整个数据集上的函数f做积分，然后再除以这个集合的大小（也就是区域R的面积）：
上式可以看作所有点处f值的和除以所有点的个数，前提是各点的权重一致，也就是等权平均值。
如果是加权平均，还需要在积分内乘以权重系数：
其中δ权重系数，如果f是关于x和y的函数，那么δ也应当是关于x和y的函数，也就是每一个f(x,y)都有对应的δ(x,y)。
示例
如下图所示，在直角坐标系下有平面一个物体，该物体的密度是ρ = xy，求该物体的质量和质心位置。
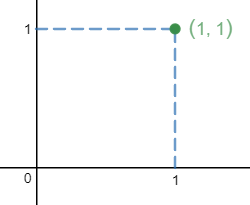
由于是平面物体，其质量是面积的积分；由于物体是不均匀的，所以还需要乘以权重：
在x方向上的质心：
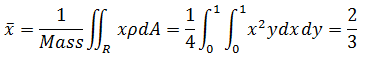
由于该物体是关于y=x对称的，所以y方向上的质心也是2/3
作者：我是8位的
出处：http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注公众号“我是8位的”
