多变量微积分笔记7——非独立变量
1．独立变量，即一个量改变不会引起除因变量以外的其他量的改变。只有将某物理量由独立变量来表达，由它给出的函数关系才是正确的。
2．非独立变量，一个量改变会引起除因变量以外的其他量改变。把非独立变量看做是独立变量，是确定物理量间关系的一大忌。
正确确定物理表达式中的物理量是常量还是变量，是独立变量还是非独立变量，不但是正确解答有关问题的前提和保障，而且还可以简化解答过程。
在理想的气体状态方程中，PV/T=C，其中C为常数。可以将其看作一个约束关系g(P,V,T) = C，当其中一个变量改变时，也必将引起其它两个变量的改变，P、V、T就是g的三个非独立变量。
非独立变量的变化
如果有一个包含三个非独立变量的函数 g(x,y,z) = C，理论上每一个变量都可以用另外两个变量表示，例如z用x,y表示：z = z(x,y)，这样就可以更加清晰的知道z与x,y的关系，即当x,y变化时是怎样影响z的。然而在大多数情况下，求解z(x,y)都比较困难，这时应当怎样理解变量之间的关系呢？也就是在z = z(x,y)中，z的变化率是多少？
有一个关系式 g(x,y,z) = x2 + yz + z3 = 8，在点(x,y,z) = (2, 3, 1)附近观察，如果稍微改动x和y，x和y对于z的变化有什么样的影响？
在这里，直接解出z的表达式会很困难，需要寻找一个更简单的方法。
先来看一下g的全微分（全微分可参考《多变量微积分4——全微分与链式法则》）：
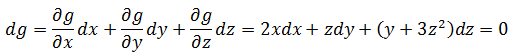
由于g(x,y,z) = C = 8，所以dg = 0；或者说由于g(x,y,z) 是一个常数，g的变化率为0。在(x,y,z) = (2, 3, 1)处：
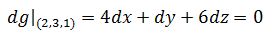
这个式子告诉我们，在等值面上变化量之间的关系，其中两个变量改变时，第三个变量会怎样变化。如果把z看成x,y的函数z = z(x,y)，z的变化：
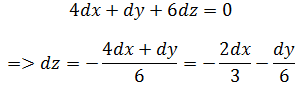
z关于x的变化率就是x的偏导，此时y值不变，dy = 0：
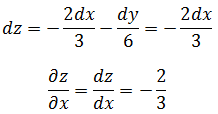
z关于y的变化率就是y的偏导，此时x值不变，dx = 0：
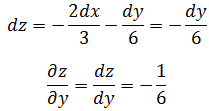
一般地，如果g(x,y,z) = C，那么：
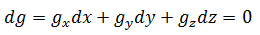
这样任何变量的微分都可以由其它变量表示，例如z的变化：
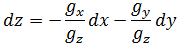
z关于x的偏导，y是定值，dy = 0，此时：
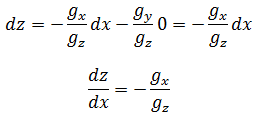
这个结果就是当x改变时，x对于z的变化率，即：
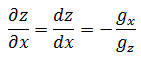
同理：
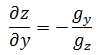
通过这种方式，可以表达非独立变量之间的变化。
相关变量的偏微分
有一个函数f(x,y) = x + y，现在x的偏导：
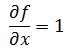
如果令x = u, y = u + v：
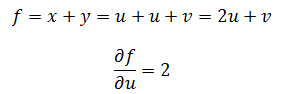
现在的结果有些令人迷惑了，因为x = u，所以x和u等价，但是得到的结果并不相同：
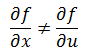
这点在《多变量微积分4——全微分与链式法则》中做过介绍，实际上：
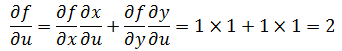
这需要认真审视偏导，当计算fx时，意味着保持y不变的同时改变x；而fu意味着保持v不变的同时改变u。由于x = u，所以改变u和改变x是一样的，但保持v不变和保持y不变并不相同。如果保持y不变，因为x = u，所以改变x的同时也意味着改变了u，所以为了保持y不变，v也势必发生改变，从而使y = u + v不变。当保持v不变时，v = y – u = y – x，可以看出，保持v不变实际上是保持y – x不变，这和保持y不变是两回事。这些偏导虽然看似简单，但使用起来其实是有风险的，因为让它们保持恒定并不是显而易见的。
现在，我们用新的符号明确是指出谁是恒定不变的：
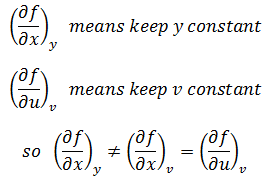
三角形的面积
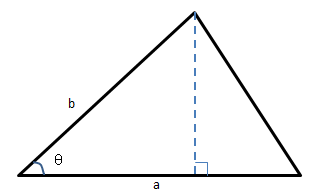
三角形的两边分别是a和b，ab的夹角是θ，面积A = (absinθ)/2，可以将其看作是关于a、b、θ的函数A(a,b,θ)。假定三个变量之间存在某种约束关系，比如三角形是直角三角形，那么a = bcosθ就是变量之间的约束，现在我们想知道面积是怎样依赖于θ的？
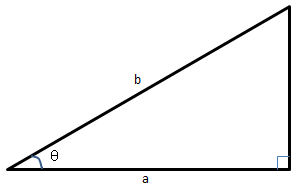
面积关于θ的变化率当然是面积A关于θ的偏导，问题是a,b,θ不是相互独立的变量，直角三角形就是三者之间的约束，当θ改变时，为了维持直角，a或b也会随之改变。下面将分情况加以说明。
1） a,b保持不变
实际上这意味着放弃直角这一约束。如果保留直角，将有两个选择，保持b恒定或a恒定。
2） a保持不变，θ改变时，面积的变化率是：
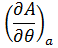
3） b保持不变，θ改变时，面积的变化率是：
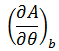
现在需要进行一些计算，以第二种情况为例，看看面积的变化率具体是什么。
方法1）利用最简单的代数法，这种方法仅对于简单的约束关系有效。
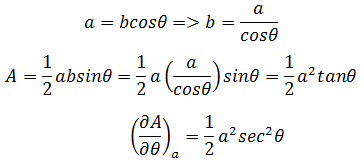
方法2）微分法
如果保持a不变，意味着da = 0
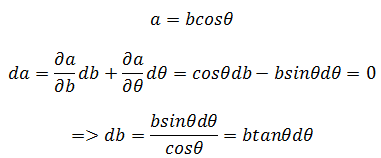
这实际上是求出了b关于θ的变化率。
这个结果就是当a保持不变时，A对于θ的变化率，即：
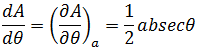
结果中含有b是因为改变θ的同时b也将发生改变，因此b也要被看作因变量。
综合示例
示例1
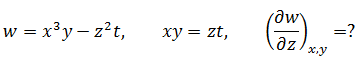
示例中的约束条件是xy = zt，可将其看作g(x,y,z,t) = xy – zt = 0，在假定x,y不变的前提下计算w关于z的变化率。
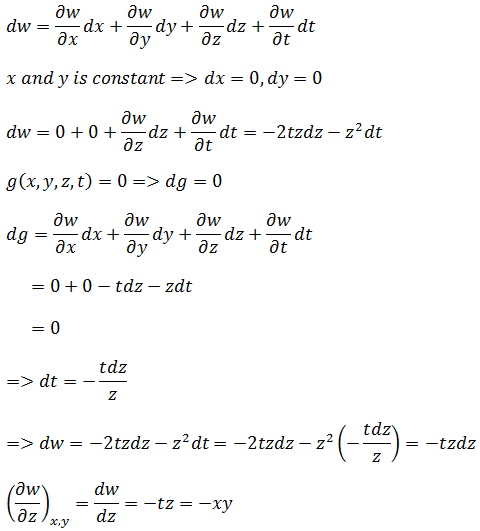
示例2
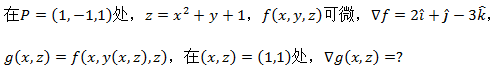
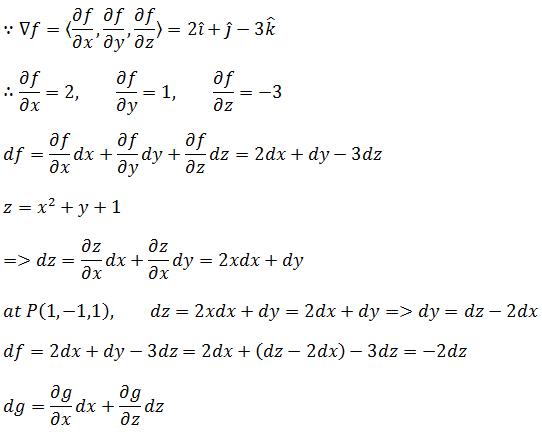
作者：我是8位的
出处：http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
