多变量微积分笔记2——最小二乘法
回归分析
回归分析是一种预测性的建模技术，用于连续性数据的机器学习（在监督学习中，如果预测的变量是离散的，称其为分类；如果预测的变量是连续的，称其为回归），它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。
一元线性回归
在机器学习中，一元线性回归是回归分析中最简单的一种，它有一个自变量和一个因变量，它是这样描述的：如果能够一系列训练数据(x1, y1), (x2, y2)…(xn, yn)寻找出一条最佳拟合直线y = ax + b，用这条直线近似地表示x和y的关系，那么这种分析就称为一元线性回归分析。
多元线性回归
多元线性回归和一元线性回归本质上是一样的，只不过数据样本有n个维度（或称为n个特征向量），即：
这里x的上标表示第i个样本集。线性回归的目的是找到x的系数θ：
通过求解θ得到最终的拟合曲线，也就是预测模型：
简写为：
这正是y = ax的形式。如果令x0 = 1，则多元线性回归就可看作一条直线y = ax + b，实际上，多元线性回归是n维空间的一个超平面。
误差的计算
一元线性回归的目标是找到最佳的a和b，这里“最佳”是说我们找出的这组a和b能使得所有训练数据误差的总和达到最小化。
计算误差的办法有很多种，其中两种典型的做法，一是计算数据到直线的距离，二是数据和直线所对应的y值。根据计算方法的不同，得到的最终训练模型也不同。
实际应用中，如果计算点到直线的距离，就需使用两个维度的数据进行计算，而实际上两个维度大多数时候都不存在直接的计算关系，比如时间和房价，二者并不能直接进行加减运算，想要运算必须通过成本函数转换。基于上述原因，通常使用第二种方法，也就是计算数据和直线所对应的y值：
最小二乘
找到最佳拟合直线的方法有很多，其中一种就是最小二乘法。
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。最小二乘法的计算公式：
其中h是预期模型，h(xi)是模型预测的结果，yi是实际结果。对于一元线性回归来说：
D(a, b)是关于a和b的函数，把xi和yi代入到最小二乘法的式子中，就得到了一个关于a和b的方程。在这个方程中，a和b是未知数，x和y是已知数。使D(a, b)最小的方法就是找到临界点，也就是D关于a的偏导和D关于b的偏导同时等于0的点：
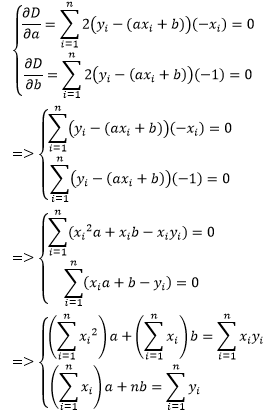
这就是最终的方程组，可以根据该方程组求出a和b。可以看到，如果数据集的不同，求出的a和b也不同，也就是最终的预测模型不同。
示例
用最小二乘法把下列数据拟合成直线和曲线，(0, 1), (2, 1), (3, 4)
最佳拟合直线是y = 6x/7 + 4/7
如果拟合为曲线，则y = ax2 + bx +c，
将(0, 1), (2, 1), (3, 4)代入方程：
为了把这个无聊的方程交给计算机处理，将其变为矩阵方程：
1 import numpy as np
2
3 a = np.matrix([[97,35,13],[35,13,5],[13,5,3]]) ** (-1)
4 b = np.matrix([[40],[14],[6]])
5 print(a * b)
最终的拟合曲线是y = x2 –2x + 1
可以看出，三个点全部在曲线上，最小误差是0。这实际上正是期望的结果，因为训练数据只有三个点，所以根据这三个点得到的三元一次方程组：
这也从侧面反映出最小二乘法的正确性。
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
