单变量微积分笔记29——反常积分和瑕积分
我们已经学习了有限区间上的积分，但对于无穷的情况和区间上有奇点的情况仍无法理解。这就需要无穷积分和瑕积分来处理了，它们看起来十分有趣。
增长和衰减速率
通过上一章的内容，我们已经可以做出一些总结，在洛必达法则中，如果f(x) << g(x)且f,g > 0，那么当x→∞时，f(x)/g(x)→0；如果f(x) >> g(x) 且f,g > 0，那么当x→∞时，f(x)/g(x)→∞
反常积分
收敛和发散
反常积分是这样定义的：
从定义来看，也就是正常积分的上限N趋于∞。如果极限存在，它就是收敛的，否则就是发散的。
积分表示面积，在收敛的情况下，面积是有限的，如下图所示，面积最终将趋于定值：
在发散的情况下，面积是无限的，比如一条与x轴平行的直线。
计算反常积分
示例1：
也可以采用一种更简短的写法：
示例2：
在上限是∞的时候，1/x的积分是发散的。这似乎与直觉相反，虽然被积函数f(x) = 1/x随着x的递增而减小，但它的衰减速度还不够“快”，它仍然是发散的。
示例3：
到这里就可以结束了，如果我们还想继续探索一下，就要看看P的取值范围。首先p的值不能为1，当p < 1时，
当p > 1时，
对于该例来说，p < 1时是发散的，p > 1时时收敛的。
审敛法
我们通常对反常积分是发散还是收敛很感兴趣，然而计算极限往往令人沮丧，幸而我们了解增长和衰减速率，将被积函数替换成更快或更慢的函数，以此判断反常积分的收敛性，这种方法就是审敛法。
审敛法大概是这样描述的：
当x→∞且f,g ≥0时，
- 如果f(x) ∽ g(x)，即f(x)/g(x)→1，则
- 如果g(x) >> f(x)且
是收敛的，则
也是收敛的 - 如果g(x) << f(x)且
是发散的，则
也是发散的
示例1
判断 
的收敛性
如果求解原函数，就需要动用三角替换，经过一些列转换后再求解极限，可能还要使用洛必达法则……现在尝试使用审敛法判断。
所以答案是发散的。
这里需要注意的是，相似的反常积分的下限是1。这么做有两点原因，第一点当然是分母不能为0；第二点是，当上限为∞是，下限不构成影响结果的主要因素。在反常积分中，我们关注的是趋于∞的尾端。将下限写为1仅仅是便于理解和书写，实际上可以写成大于0的任意数。
示例2
判断
的收敛性
结果是收敛的。
示例3
判断
的收敛性
结果是收敛的，其中用到的衰减率是 1 ≤ x ≤ x2，- x2 ≤ -x
瑕积分
定积分的奇点
这很简单，
这个答案对吗？
我们熟知1/x2的图像，积分表示面积，那么它不可能是负数，一定是哪个环节出现了问题。
如果只计算x ≥ 0时的面积：
这个结果是无意义的，对1/x2在[0,1]上积分没有任何意义。换个角度看这个问题，假设积分下限是是一个无限接近0的数值，结果趋近于∞，这个积分是发散的。
在这个例子中，将0称为积分的奇点，对于不同的积分来说，奇点也不同。积分在奇点上是无意义的。
结论是，如果我们这计算时不注意积分的奇点，很容易导致计算错误。看来在今后的积分运算中又多了一条注意事项。
瑕积分的定义
将存在奇点的积分称为瑕积分，用数学符号表示就是：
需要注意的是a是从右侧接近0，这实际上和处理无穷的思路是一样的。
就是一个典型的瑕积分，奇点是0，结果是∞。
收敛和发散
与反常积分一样，我们关注的是瑕积分在奇点的收敛性。
当x→0+时：
当x→+∞时：
这里用红色的被积函数表示发散，绿色表示收敛，很容易对其进行计算。
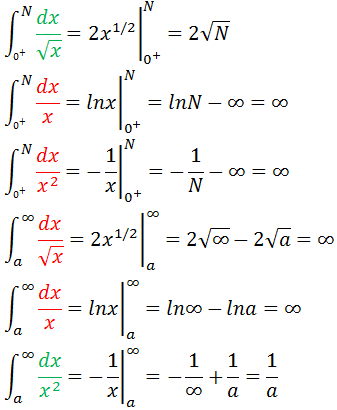
可以通过图像直观地了解一下：
示例
判断
的收敛性
看起来很简单，
当x→∞时，1/x2的积分是收敛的，所有结论是收敛。
真相确实如此吗？1/(x – 3)2的图像如下：
看起来没那么简单了，答案应该是发散才对。问题的原因就在于积分存在奇点，就是x = 3。一个简单的判定奇点判定法是当x = 3时被积函数没有意义。
等式右侧的第一个积分跨越了奇点，在奇点一节中提到过：积分在奇点上是无意义的，如果一个积分跨越了奇点，那么这个积分就是发散的。所以最后答案是发散。
综合示例
示例1
判断积分的收敛性
其结果是在-1和1之间波动，所以题目积分是不可积的。
更简单的方法是在0和∞之间，cosx的图像是来回摆动的，并未趋近于某个值，可以直接得出不可积的结论。
示例2
判断积分的收敛性
积分的奇点是0，需要判断这奇点上是否是收敛的。
先用分部积分求解，
极限是0·∞型，需要对其进行转换以便使用洛必达法则，
题目积分在奇点收敛于0，最终收敛于-4。
示例3
判断积分的收敛性
积分的奇点是0，积分跨越了奇点，需要分成两半：
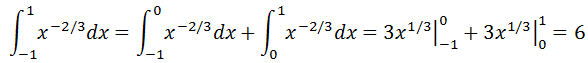
题目积分在奇点收敛于0，最终收敛于6。
示例4
曲线f(x) = 1/x绕x轴旋转，求x在[1, ∞)上形成图形的表面积和体积。
上面的计算通过弧长计算表面积（弧长和表面积可参见数学笔记25——弧长和曲面面积），再利用审敛法求反常积分。这看起来没什么问题，但是有些繁琐。由于我们已经知道1/x在x→∞上是发散的，所以可以直接判断表面积也发散。
根据圆盘法（圆盘法可参见数学笔记17——定积分的应用2（体积））求计算体积：
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
