单变量微积分笔记25——弧长和曲面面积
积分的概念来源于实际应用。对一个函数积分可以理解为求曲线下的面积，但积分的作用不仅仅如此。作为牛顿一生最伟大的发明，有了积分，我们就可以去计算曲线的弧长，可以去求区域的面积，也可以去计算很多物理问题。
弧长
弧长的定义
曲线上两点之间的曲线长度称为弧长，现在我们试图用积分定义弧长。
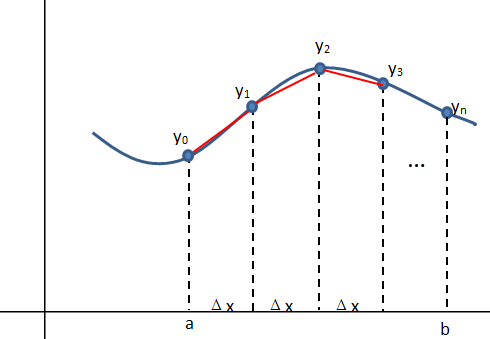
将上图的曲线分为n段，用直线连接相邻的两点，当Δx→0时，两点间的线段长度趋近于弧长：
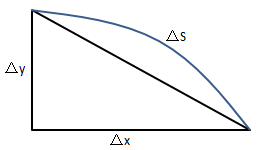
将s定义为弧长，则：
用微分表示上式，可以去掉约等号：
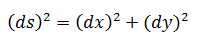
习惯上，上式去掉括号：
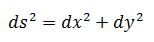
其它两种常见的变形：
由此得到a、b两点间弧长的表达式：
线性函数的弧长
如果有曲线y = mx，则y’ = m，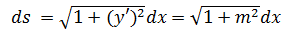 
，曲线在0 ≤ x ≤ 10处的弧长：
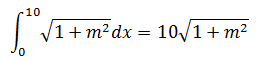
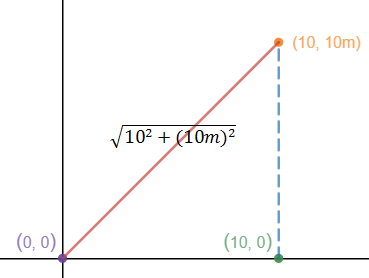
如上图所示，可以抛开积分直接计算两点间的弧长，其结果和积分运算相等。对于这个例子来说，结果是显然的，但是其表达的含义是：如果我们能对线性函数推导出这些公式，那么微积分也能告诉我们应该怎么做。微积分的思想就存在于这个简单的，甚至不需要微积分计算的过程中。所有这些工具，微分、积分、极限，可以应对任何曲线，因为我们将曲线分割成了无限小，这就是建立积分的思想。
单位圆的弧长
计算下图单位圆上的弧长s：
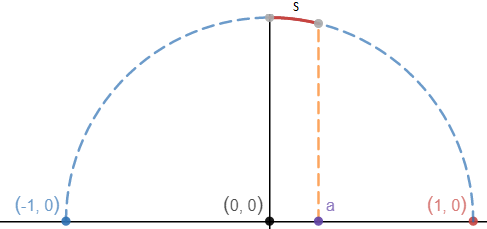
单位圆中：
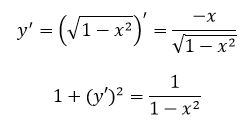
根据弧长公式：
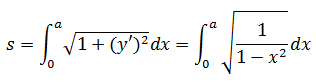
接下来就是求解积分的问题。
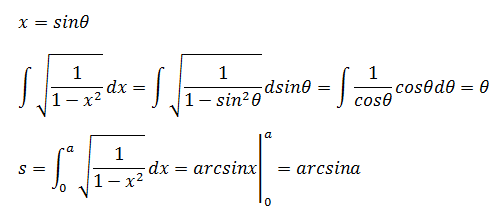
也可以写成：a = sins
在单位圆中，弧长s = 弧长夹角θ，a = rsinθ = sinθ，上面的计算结果与定义相同。
抛物线的弧
求曲线y = x2在x∈[0, a]上的弧长。
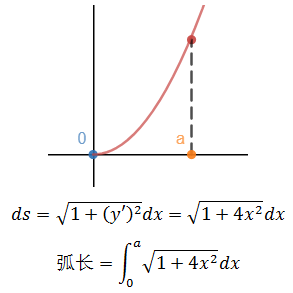
接下来是求解积分问题，令x = tanθ/2
令u = secθ， v’ = sec2θ， v = tanθ, u’ = secθtanθ
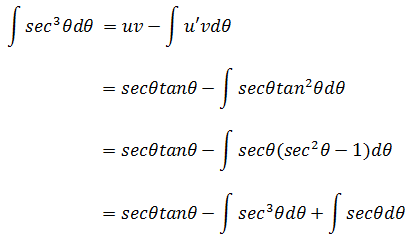
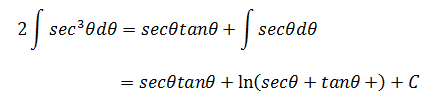
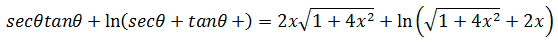
最终弧长：
曲面面积
求解方法
曲线y = x2绕x轴旋转一周，求在x在[0, a]上，立体图形的外表面积。
图形类似于喇叭口，可以使用圆盘法求解，只是将dx换成ds，上图中圆盘的表面积：
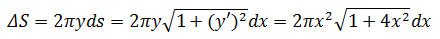
总面积：
这个复杂的积分还是交给计算机吧。
球面面积
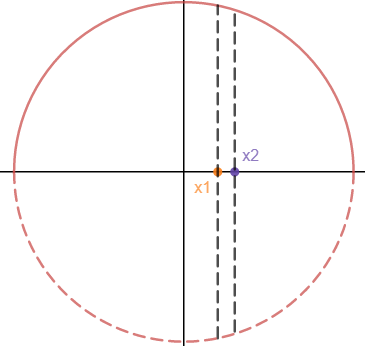
可以将球看作为半径为a的半圆y2 + x2 = a2绕x轴旋转一周形成的图形，计算x在[x1, x2]处形成圆盘的球面面积：
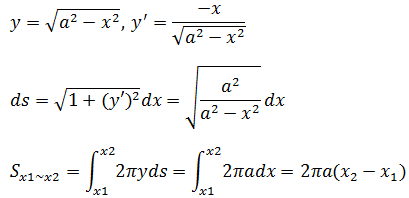
整个球体的表面积：
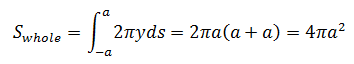
结果与球体表面积公式一致。
综合示例
示例1
计算y = x3/2在0 ≤ x ≤ 4处的弧长。
y = x3/2
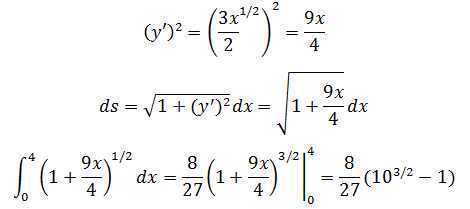
示例2
如下图所示，求圆心为R，半径为r的圆绕y轴旋转一周形成的环的表面积
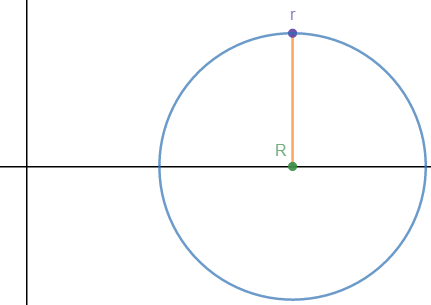
由于是绕y轴旋转，表面积的微分是da = 2πxds，接下来就是如何求解ds和da的积分。
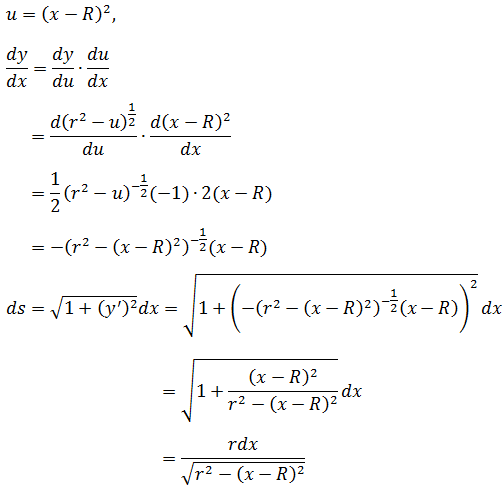
上半圆的表面积：
又是求解积分的问题了，令u = x - R
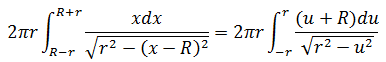
令u = rsint，du = rcostdt；u的取值范围是[r, -r]，所以t的取值范围是[π/2, -π/2]
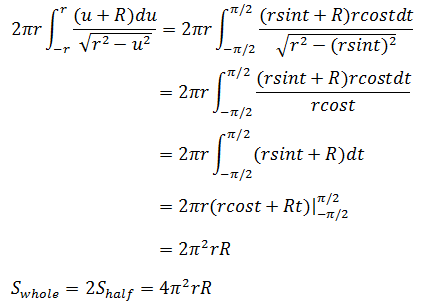
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
