单变量微积分笔记24——分部积分

　　不是所有被积函数都能解析地写出原函数。对于那些可能写出来的函数，也需要一定的积分技巧才能随心所欲，分部积分正是其中很重要的一种技巧。

基本公式

　　部分积分演变自积分的乘法法则：

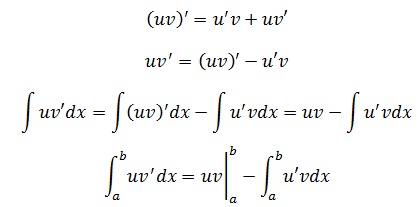
示例1

 

　　看起来很难对付，现在尝试用部分积分解决。

　　令u = lnx，u’ = (lnx)’ = x’/x = 1/x 

　　令v’ = 1，v = x，u’v = 1

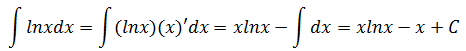
示例2

 

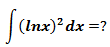
　　解法1：

　　令u = (lnx)²，u’ = 2lnx/x 

　　令v’ = 1，v = x，u’v = 2lnx/x

 

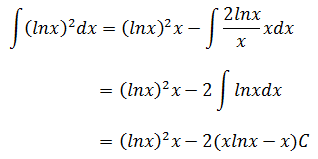
　　解法2：

　　令u = lnx，u’ = (lnx)’ = x’/x = 1/x 

　　v’ = lnx，通过示例1得知，v = xlnx – x

　　u’v = lnx - 1

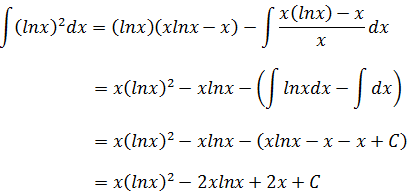
换算公式

　　换算公式使用递归的方式运用部分积分公式，最终得到结果。

 

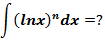
　　这与前面的示例类似：

　　令u = (lnx)ⁿ，u’ = n(lnx)^n-1/x 

　　令v’ = 1，v = x，u’v = n(lnx)^n-1, uv = x (lnx)ⁿ

 

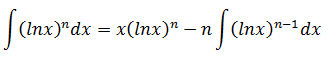
　　再对后半部分反复使用分部积分，使lnx降次，直到其为0为止。如果用F_n(x)表示(lnx)ⁿ的积分，则：

 

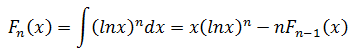
　　根据该公式：

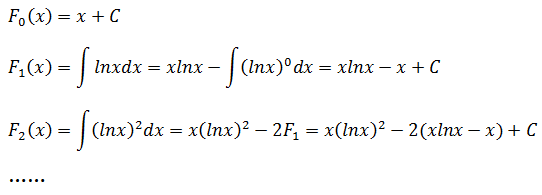
示例1

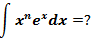
　　令u = xⁿ，u’ = nx^n-1

　　令v’ = e^x，v = e^x，u’v = nx^n-1e^x, uv = xⁿe^x

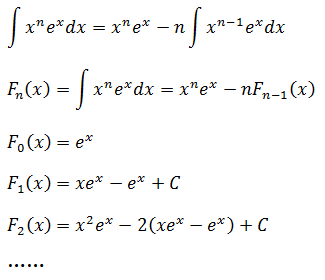
示例2

　　有如下图所示的高脚杯，其侧壁的曲线函数是y = e^x，开口宽度为2，手柄高度为1，求高脚杯的容积。

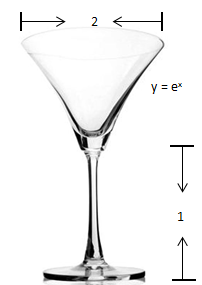
求高脚杯容积

　　首先将其转换为下图所示的数学模型，容积就是曲线绕y轴旋转一周的体积：

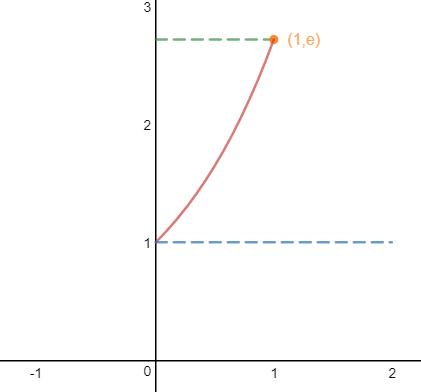
　　可以使用圆盘法和壳层法计算体积（可参考数学笔记17——定积分的应用2（体积））。

　　圆盘法：

　　壳层法：

 

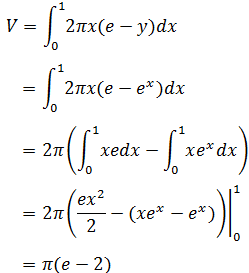
综合示例

示例1

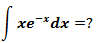
　　令u = x，u’ = 1

　　令v’ = e^-x，v = -e^-x，u’v = -e^-x，uv = -xe^-x

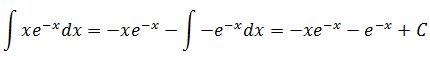
示例2

　　解法1：分部积分

 

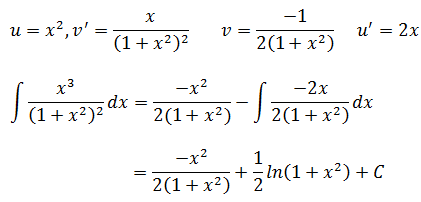
　　解法2：部分分式

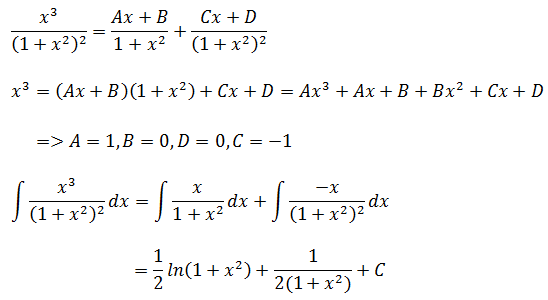
　　解法3：三角替换，令x = tanθ

 

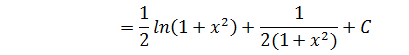
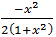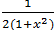　　注意到解法1和后两种方法的结果不同，但由于 和 的导数相同，所以二者是等同的。

　　也可以从另一个角度证明，现在回顾一下解法3：

 

　　如果替换为sinθd的函数，则： 

 

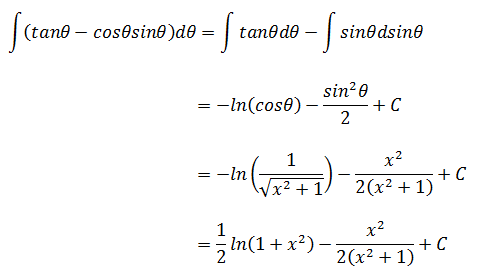
　　所以两个结果相等。

　　实际上两个函数是同族的：

 

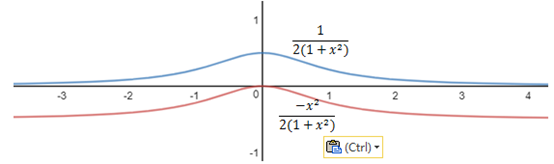
示例3

 

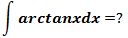
　　u = arctanx, u’ = 1/(1 + x²), v’ = 1, v = x

　　下面是arctanx的求导过程：

　　y = arctanx, x = tany, 对x = tany两边同时对x求导：

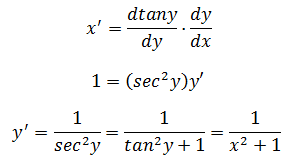
　　关于反函数的求导，可参考数学笔记4——导数4（反函数的导数）。

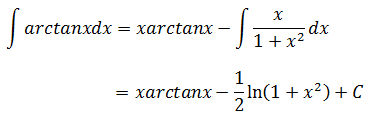
示例4

 

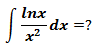
　　u = lnx, u’ = 1/x, v’ = x^-2, v = -1/x。

 

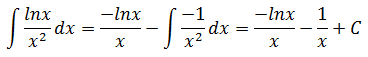
示例5

 

 

---

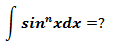
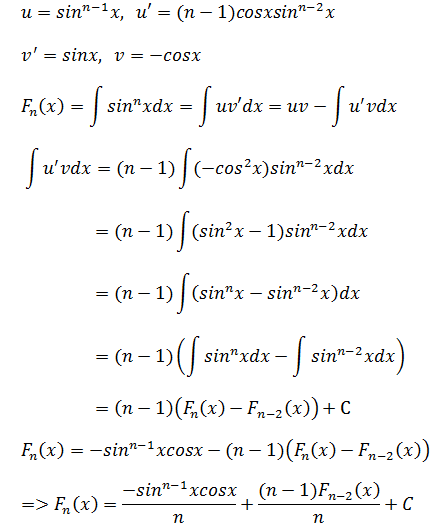
　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”