单变量微积分笔记22——三角替换3（反向替换和配方）

反向替换

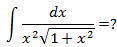
　　若想求解，就必须去掉根号，但是现在发现没法用以往的知识求解了。

　　现在尝试求助于三角函数。在上篇文章中，我们提到：

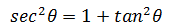
　　这正好吻合根号下的表达式。现在令 x = tanθ，则：

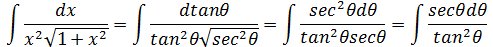
　　在三角函数中，只有sin和cos是比较友好的，其它都是变态。所以除非一眼能看出如何简化，否则应该把所有项都写成sin和cos的形式。

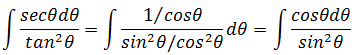
　　已经变成熟悉的三角函数积分了。

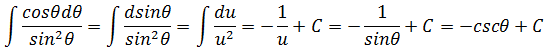
　　现在的问题是如何将θ转换为x。这需要求助于三角函数的几何意义，实际上已经使用过多次，如下图所示：

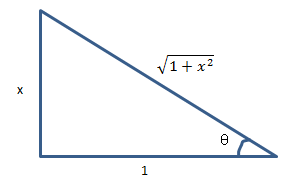
　　由上图可知：，最终，经过反向替换：

三角替换的基本套路

配方

　　很多时候，根号下的表达式并不是上面表格中的标准套路，这就需要使用配方法将其凑成标准套路。

 

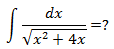
　　如果根号下是x²+4就好办了。我们的目标是将其变成标准套路中的一种，然后使用三角替换将根号去掉。

　　现在，结果符合标准套路了

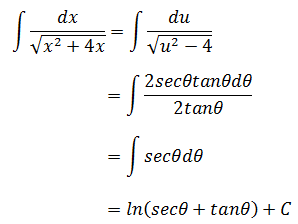
　　最后需要利用反向替换将θ转换为x。

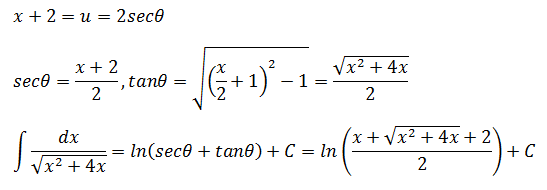
示例

　　根号下的东西看起来能够凑成平方差：

 

　　根据套路3进行配方：

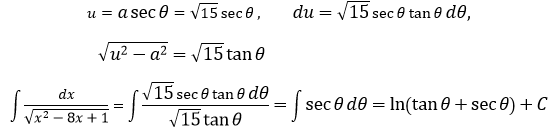
 　　最后根据三角函数的几何意义将θ替换回x：

 

---

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”