单变量微积分笔记17——定积分的应用2（体积）
定积分除了计算面积外，还可以应用在计算体积上。
圆盘法
一条曲线y = f(x)，如果曲线绕x轴旋转，则曲线经过的区域将形成一个橄榄球形状的体积，如下图所示：
曲线绕x轴旋转一周
现在要计算体积。我们依然按照黎曼和切片的思路去计算，只不过这回需要一点想象力。
将上图的矩形绕x轴旋转一周将得到一个半径为y，高度为dx的圆盘：
矩形框绕x轴旋转一周
该圆盘的面积S(x)≈π(f(x))2，体积： Δv ≈ S(x)Δx，如果将整个图形的体积切成n个圆盘：
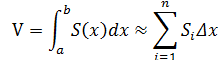
这就是圆盘法。
示例
求半径为a的球的体积。
通过球体的公式可知，V =πa3(4/3)，假设我们不知道这个公式，使用圆盘法求解。
先将球体的最大横截面投影到直角坐标系上，在对圆的上半部分切割，旋转，如下图所示：
圆盘的底面积≈πy2，由此可以得到球体体积：
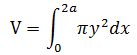
还需要将y转换为x。根据上图中圆的公式(x – a)2 + y2 = a2，可得出y2 = 2ax - x2，于是：
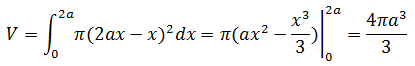
实际上我们得到了更多的信息，如果仅计算部分球体的体积，依然可以使用上面的结论，仅改变积分上限即可，如下图所示：
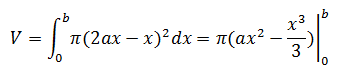
实际上可以把V = π(ax2 – x3/3)看作球体切片的公式。
壳层法
假设坩埚内壁的横截面曲线是y = x2，深度是a，计算坩埚的容积。
计算坩埚的容积
我们依旧可以使用圆盘法计算，这是这次是绕y轴旋转：
圆盘法
圆盘的高度是Δy，所以需要将原函数转换成y关于x的函数，在正半轴上，x = y1/2
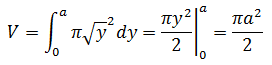
对于本例来说，圆盘法没有问题，如果曲线的公式再复杂一点，就需要在反函数的转换上耗费时间，如果我们直接纵向切割，使用dx代替dy，就无需对原函数进行转换：
矩形绕y轴旋转一周将得到一个圆环，其厚度是dx，半径是x，高度是a – x2，如下图所示：
如果展开圆环，将得到一个底面积是圆环周长，高度是dx的长方体，其体积：
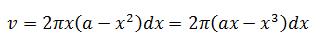
由此，坩埚的容积是：
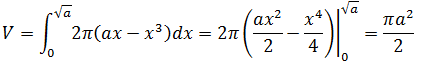
单位产生的悖论
在计算坩埚的容积时，我们最终得到V = πa2/2，如果坩埚深度是1m，代入公式得到π/2（m3）；现在将1m换成100cm，因为高度是一样的，所以我们期待得到同样的结果，但是代入公式后，最终得到10000π/2（cm3）= 0.01π/2（m3）相差了100倍！这回有意思了。
问题出在哪呢？仔细观察最终结果的积分形式：
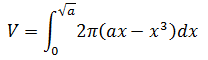
积分的上限是a1/2，11/2 = 1，1001/2 = 10，因此单位不同将得到不同的结果。实际上这个公式违背了比例原则，将所有问题数学化的同时并没有考虑到物理学中的量纲。这就好比重力加速度是9.8，但这个9.8是有单位的，单位是米每二次方秒，如果长度单位采用厘米，这个常数9.8也需要相应变化才能适用。
示例
示例1
求y = 5和y=x2 + 1所围图形绕y轴旋转后得到的体积。
用圆盘法计算，圆盘绕y轴旋转，如下图所示：
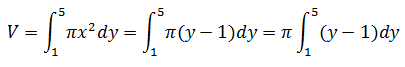
示例2
求x=4和y=x1/2，x轴所围图形绕x=6旋转后得到的体积。
本例根据壳层法计算，如下图所示：
壳层（或圆环）的高是x1/2，半径是6 – x，厚度是dx：
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
