单变量微积分笔记13——定积分

　　定积分是积分的一种，是函数f(x)在区间[a,b]上的积分和的极限。这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值（曲边梯形的面积），而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式），其它一点关系都没有！一个函数，可以存在不定积分，而不存在定积分，也可以存在定积分，而不存在不定积分。一个连续函数，一定存在定积分和不定积分；若只有有限个间断点，则定积分存在；若有跳跃间断点，则原函数一定不存在，即不定积分一定不存在。

什么是定积分

　　有一块形状不规则的土地，要测量它的面积，怎么办呢？

 

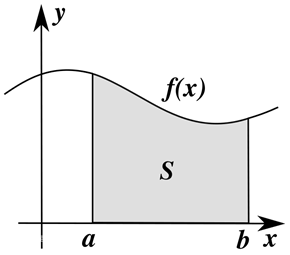
　　这意味着我们要求解曲线下的面积，该面积从a开始，到b结束，用 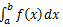表示，这就是定积分。对比不定积分，发现定积分有起点和终点。不定积分是已知导数求原函数，定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。即由 y=0,x=a,x=b,y=f(X)所围成图形的面积。

黎曼和

　　如何求解曲线下的面积呢？为了简化问题，我们假设f(x) = x²，这是一个较为简单的曲线，同时设a = 0， b = 1：

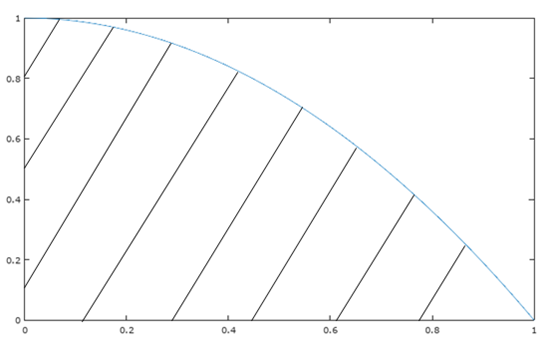
　　分为三步计算面积：

1. 首先把阴影部分却成一系列等宽的矩形；
2. 把这些矩形的面积加起来：
3. 修正之前的算法。

　　如下图所示：

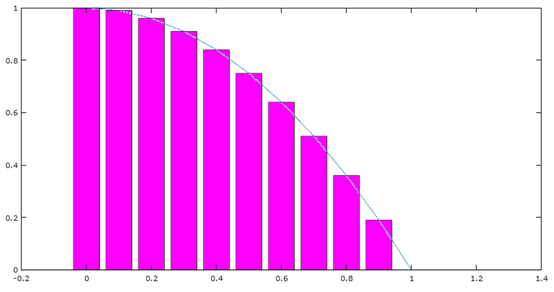
将面积分为成一系列矩形

　　我们看到，每个矩形都可能超出或小于实际面积，所谓“修正之前的算法”，是修正矩形增加或减少的面积，具体做法是通过让矩形变窄来取得极限值，如下图所示：

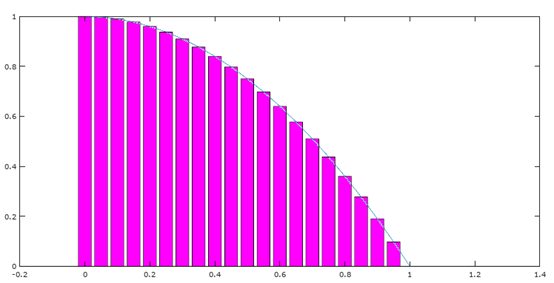
矩形变窄

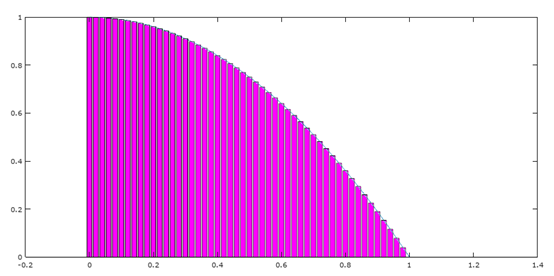
变得更窄的矩形

　　矩形越窄，就越接近实际面积。

　　当矩形宽度很小时，把所有矩型面积加起来就是这块不规则图形的面积，这就是著名的“黎曼和”。矩形宽度趋于0时，即为面积微分；各个面积求和取极限即为定积分。虽然牛顿时代就给出了定积分的定义，但是定积分的现代数学定义却是用黎曼和的极限给出。

　　就上图而言，f(x) = x²，a = 0，把ab分为n份：

　　曲线下的面积之和就是当n→∞时的矩形面积之和。现在的问题是如何求得(1²+2²+3²+...+n²)/n³。

　　这需要一点技巧，用作图法求解。

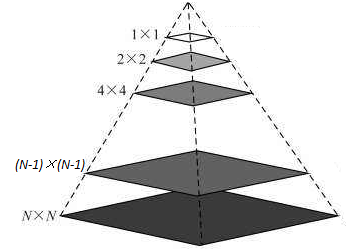
　　想象一下金字塔，每一层都是有若干块砖头堆砌而成，其模型如下：

　　垂直切割面如下面两图所示：

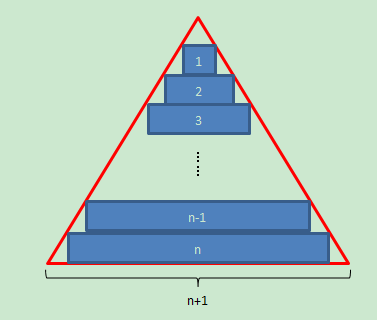
图1 三角形面积大于金字塔面积

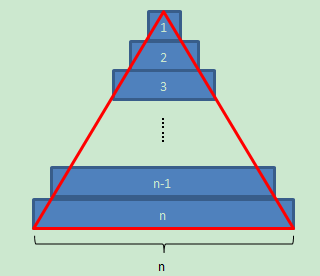
图2 三角形面积小于金字塔面积

　　由此可以将问题转换为求金字塔的体积。

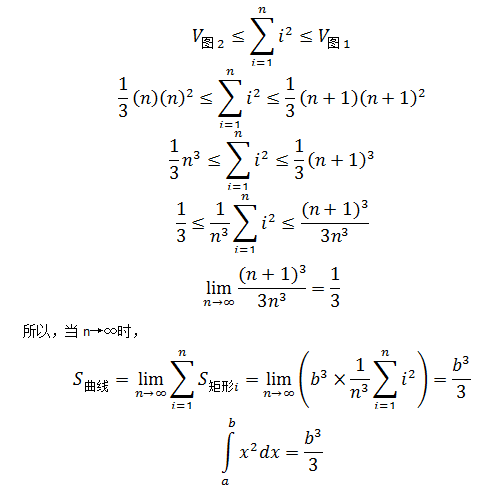
面积的示例

三角形的面积

　　f(x) = x，求阴影部分三角形面积。

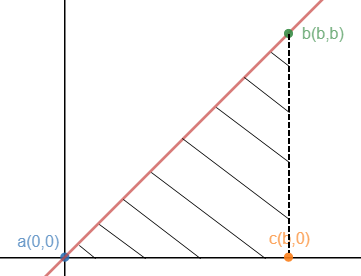
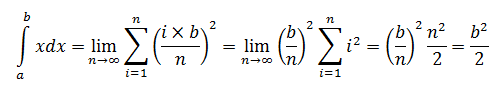
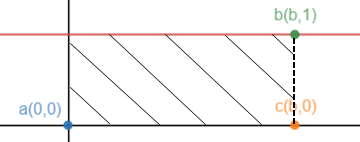
长方形的面积

　　f(x) = 1，求阴影部分长方形的面积。

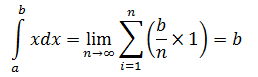
定积分的公式

　　结合上面的例子，设Δx = (b - a)/n，给出定积分公式：

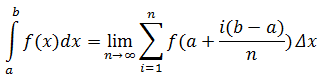
　　可以得到下面的表格：

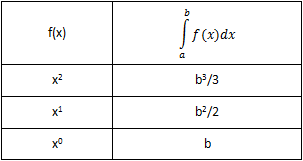
　　可以大胆地猜测，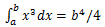

示例

　　估算f(x) = x3在[-1, 3]上的定积分。

　　设Δx = 1，

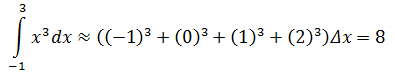
 总结

1. 定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。
2. 当矩形面积很小时，把所有矩型面积加起来就是这块不规则图形的面积，这就是著名的“黎曼和”。
3. 定积分公式：

 

---

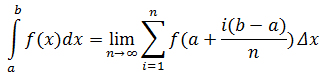
　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”