单变量微积分笔记12——常微分方程和分离变量

 常微分方程

　　含有未知函数的导数，如

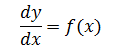
　　的方程是微分方程。 一般的，凡是表示未知函数、未知函数的导数与自变量之间的关系的方程，叫做微分方程。未知函数是一元函数的，叫常微分方程；未知函数是多元函数的叫做偏微分方程。本文主要介绍常微分方程。

　　概念往往令人迷惑，还是看看实际的例子：

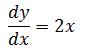
　　目标是求解x和y的关系。将等式转换：

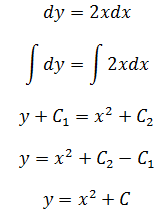
　　这就是最终答案。

　　实际上，常微分的求解过程就是利用不定积分的知识：

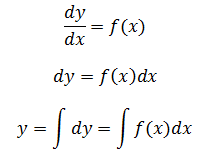
分离变量

　　分离变量是求解常微分方程的一种方法，适用于dy/dx = f(x)g(y)的形式。先看下面的示例：

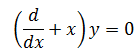
　　在物理学中它有一个专有名称，叫做“淹没算符”。此处没必要去纠结物理学概念，仅需要在数学上求解这个方程。但这个表达式和以往所见的微分表达式不一样，首先将方程展开，将其转换为我们熟悉的形式：

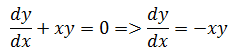
　　想要求解方程，需要继续转换：

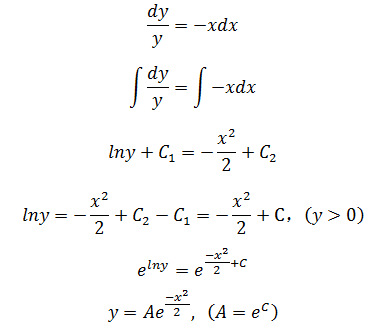
　　这就是求得的答案。

　　但上述答案只求解了y>0的情况，y≤0时尚未考虑。可以通过求导来验证答案是否是通解：

　　令a为任意常数，将解转换为y=ae^{-x^2}/2，当a≠0时，实际上a=±A

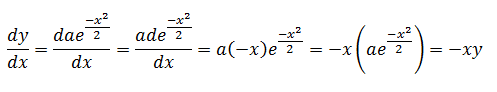
　　答案是通解，最终答案是y=ae^{-x^2}/2，a是任意常数。

　　实际上该答案就是正态分布函数，也就是著名的高斯函数，其原型：

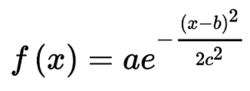
　　其中a,b,c∈R

　　高斯函数的图形在形状上像一个倒悬着的钟。a表示得到曲线的高度，b是指曲线中心线在x轴的偏移，c半峰宽度（函数峰值一半处相距的宽度）。

　　当b=0,c=0,a=5时，图像如下：

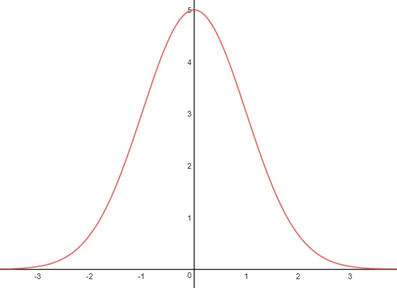
y=ae^{-x^2}/2

示例

示例1

　　曲线切线与经过原点的直线相交，曲线在交点的切线是直线斜率的两倍，求曲线表达式。

　　首先将上述文字转换为方程，设交点是(x,y)，曲线是y=f(x)，则曲线切线的斜率为y’，直线斜率为y/x，于是得到下面关系式：

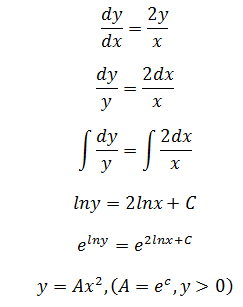
　　通过验证寻找通解，设a=±A，则a为非零的任意常数，y=ax²，验证该解：

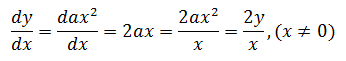
　　答案符合最初等式。最终结果是y=ax²，a∈R，x≠0

　　当a=1时，曲线y= x²，y’=2x；则在(2,4)点的切线斜率是4，切线是y=4x+b；将(2,4)代入切线，4=4×2+b，b=-4，在(2,4)点的切线为y=4x-4。下图是满足条件的曲线：

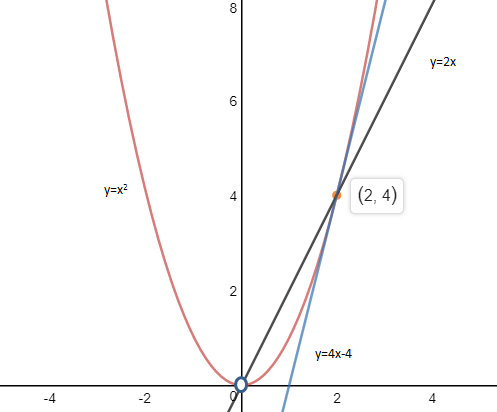
　　y=ax²实际上是一族曲线：

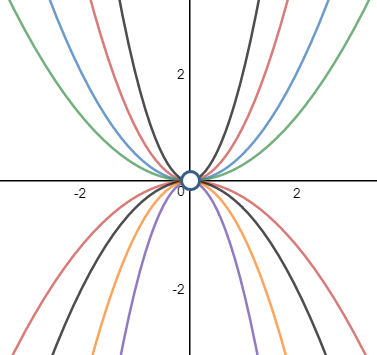
y=ax²

示例2

　　微分方程xdy/dx = (x²+x)(y²+1)，求y=f(x)

 

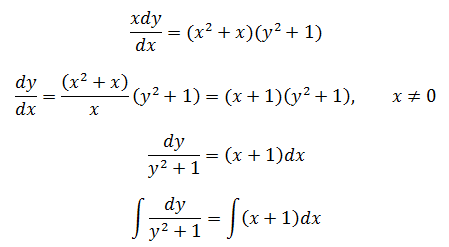
　　此处需要复习一下三角函数的求导公式：

　　由上面的公式15，

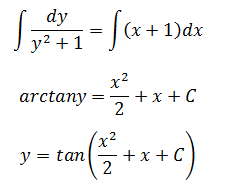
　　验证，已知三角函数公式tan²x+1=sec²x

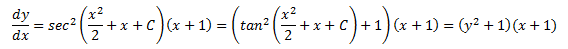
示例3

　　d²y/dx²=6x，求y=f(x)，y=f(x)在(1,1)点有水平切线。

　　题目中涉及到二阶导数和一个限制条件。

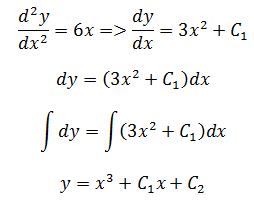
　　通过限制条件得知：

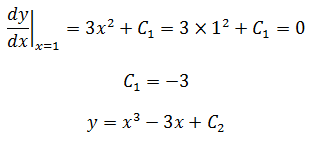
　　将(1,1)代入上式，1 = 1 – 3 + C₂，C₂ = 3

　　最终，y = x³ – 3x + 3

 总结

1. 使用不定积分求解常微分方程
2. 分离变量是求解常微分方程的一种方法，适用于dy/dx = f(x)g(y)的形式

---

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”