单变量微积分笔记9——牛顿迭代法
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
示例1:求解平方根
先来看如何用牛顿迭代法求解5的平方根。在计算器上的结果是2.236067…
问题可以看作解方程x2=5,下面尝试用牛顿迭代法求解。
首先令f(x)= x2 – 5 = 0,这是标准步骤,取得一个新函数,令该函数为0。这是一个抛物线:
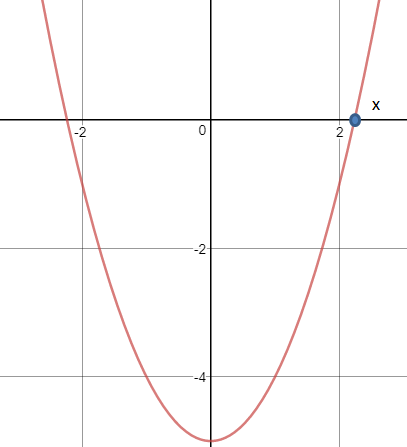
抛物线与x轴的交点x就是方程的解,它比2稍大一点。
现在在x=2处对f(x)做切线:
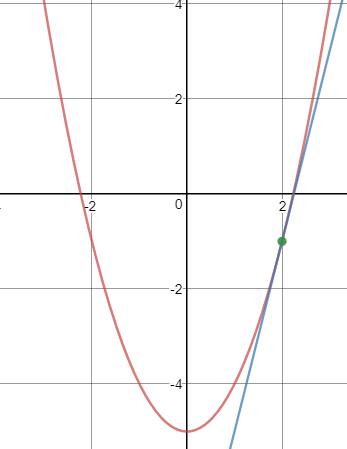
f(x)的切线
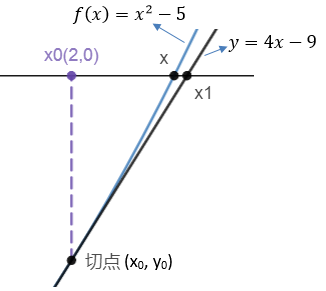
切线与x轴的交点
x0=2,y0= x02 – 5 = -1,设k是切线斜率:

在x1处做f(x)的切线,重复上面步骤,
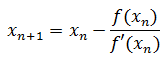
这就是牛顿迭代法的公式。通过作图可以看出,每一次迭代,x都将更靠近最终解。
f’(x)=2x,将公式代入目标方程f(x)=x2-5:

已经相当接近计算器的结果。
示例2:2cosx=3x
解方程2cosx=3x
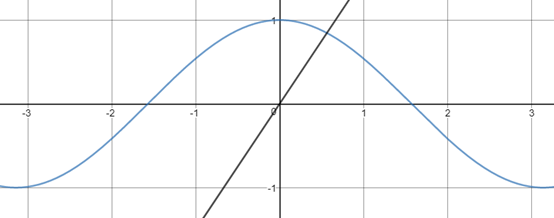
由图像可知,方程存在唯一解。
f(x)=2cosx-3x=0,f’(x)=-2sinx-3,x0=π/6≈0.52
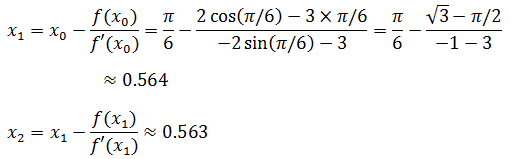
注意事项
牛顿迭代法几乎可以求解所有方程,但它仍然有一些限制。
通过前两个例子可以看到,在使用牛顿迭代法时,需要选取一个较为解接近真实解的x0作为迭代基数,x0如何选取呢?一句参考是:“f’不能太小,f’’不能太大,x0要在x附近”,这似乎要凭经验和感觉了,没有什么太好的办法;实际上,如果x0和x的差距过大,可能会得到一个没谱的解。
设第n次迭代的误差是En=|x-xn|,那么需要满足En+1<En。如果选择和计算都正确,误差缩小的速度将非常快。
以计算5的平方根为例,如果选择x0=-2,结果将偏向于-2.236067…;如果选择x0=0,则f’(0)=0,没法继续迭代,函数曲线如下图所示:
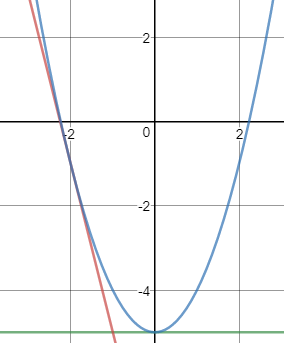
选择了错误的x0
代码示例:牛顿迭代法开平方
设x2=a,则f(x)= x2-a,根据牛顿迭代法公式:
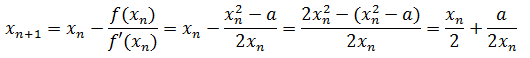
1 const float EPS = 0.00001; 2 double sqrt(double x) { 3 if(x == 0) 4 return 0; 5 double result = x; 6 double lastValue; 7 do{ 8 lastValue = result; 9 result = result / 2.0f + x / 2.0f / result; 10 }while(abs(result - lastValue) > EPS); 11 return (double)result; 12 }
上面方法开平方会很快,但 https://www.2cto.com/kf/201206/137256.html 中提到了一个更快的方法。
1999年12月,美国id Software公司发布了名为“雷神之锤III”的电子游戏。它是第一个支持软件加速的游戏,取得了极大成功。(由于影响力过大,文化部于2004年将它列入了非法游戏名单)雷神之锤III并不是id Software公司的第一次成功。早在1993年开始,这家公司就以“毁灭战士”系列游戏名闻天下。1995年,“毁灭战士”的安装数超过了当年微软的windows 95。据传比尔盖茨才曾经考虑买下id software。(id software公司后来被推出过“上古卷轴”系列的Bethesda公司买下)
id Software所取得的成功很大程度上要归功于它的创始人约翰·卡马克。马克尔也是一个著名的程序员,他是id Software游戏引擎的主要负责人。 回到刚才提到的雷神之锤,马克尔是开源软件的积极推动者,他于2005年公布了雷神之锤III的源代码。至此人们得以通过研究这款游戏引擎的源文件来查看它成功的秘密。
在其中一个名字为q_math.c的文件中发现了如下代码段:
1 float Q_rsqrt( float number ) { 2 long i; float x2, y; const float threehalfs = 1.5F; 3 x2 = number * 0.5F; 4 y = number; 5 i = * ( long * ) &y; // evil floating point bit level hacking 6 i = 0x5f3759df - ( i >> 1 ); // what the fuck? 7 y = * ( float * ) &i; 8 y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration 9 // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed 10 #ifndef Q3_VM # 11 ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE? 12 #endif 13 #endif return y; 14 }
这段代码的作用就是求number的平方根,并且返回它的倒数。
经过测试,它的效率比上述牛顿法程序要快几十倍。也比c++标准库的sqrt()函数要快好几倍。此段代码有一个奇怪的句子:
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
没错,一般的求平方根都是这么循环迭代算的但是卡马克(quake3作者)真正牛B的地方是他选择了一个神秘的常数0x5f3759df 来计算那个猜测值,就是我们加注释的那一行,那一行算出的值非常接近1/sqrt(n),这样我们只需要2次牛顿迭代就可以达到我们所需要的精度。好吧如果这个还不算NB,接着看:
普渡大学的数学家Chris Lomont看了以后觉得有趣,决定要研究一下卡马克弄出来的这个猜测值有什么奥秘。Lomont也是个牛人,在精心研究之后从理论上也推导出一个最佳猜测值,和卡马克的数字非常接近, 0x5f37642f。卡马克真牛,他是外星人吗?
传奇并没有在这里结束。Lomont计算出结果以后非常满意,于是拿自己计算出的起始值和卡马克的神秘数字做比赛,看看谁的数字能够更快更精确的求得平方根。结果是卡马克赢了... 谁也不知道卡马克是怎么找到这个数字的。
最后Lomont怒了,采用暴力方法一个数字一个数字试过来,终于找到一个比卡马克数字要好上那么一丁点的数字,虽然实际上这两个数字所产生的结果非常近似,这个暴力得出的数字是0x5f375a86。
Lomont为此写下一篇论文,"Fast Inverse Square Root"。
论文下载地址:
http://www.math.purdue.edu/~clomont/Math/Papers/2003/InvSqrt.pdf
http://www.matrix67.com/data/InvSqrt.pdf
向牛顿致敬
牛顿是近代科学的先驱,智商290,在多个领域都有非凡的成就。
他在1687年发表的论文《自然定律》里,对万有引力和三大运动定律进行了描述。这些描述奠定了此后三个世纪里物理世界的科学观点,并成为了现代工程学的基础。他通过论证开普勒行星运动定律与他的引力理论间的一致性,展示了地面物体与天体的运动都遵循着相同的自然定律;为太阳中心说提供了强有力的理论支持,并推动了科学革命。
在力学上,牛顿阐明了动量和角动量守恒的原理,提出牛顿运动定律[1] 。在光学上,他发明了反射望远镜,并基于对三棱镜将白光发散成可见光谱的观察,发展出了颜色理论。他还系统地表述了冷却定律,并研究了音速。
在数学上,牛顿与戈特弗里德·威廉·莱布尼茨分享了发展出微积分学的荣誉。他也证明了广义二项式定理,提出了“牛顿法”以趋近函数的零点,并为幂级数的研究做出了贡献。
在经济学上,牛顿提出金本位制度。
在天文成上,牛顿1672年创制了反射望远镜。他还用万有引力原理说明潮汐的各种现象,指出潮汐的大小不但同月球的位相有关,而且同太阳的方位有关。牛顿预言地球不是正球体。
在哲学成上,牛顿的哲学思想基本属于自发的唯物主义,他承认时间、空间的客观存在。如同历史上一切伟大人物一样,牛顿虽然对人类作出了巨大的贡献,但他也不能不受时代的限制。例如,他把时间、空间看作是同运动着的物质相脱离的东西,提出了所谓绝对时间和绝对空间的概念;他对那些暂时无法解释的自然现象归结为上帝的安排,提出一切行星都是在某种外来的“第一推动力”作用下才开始运动的说法。《自然哲学的数学原理》牛顿最重要的著作,1687年出版。
向伟大的牛顿致敬!
总结
- 牛顿迭代法的公式:
- 注意事项,f’不能太小,f’’不能太大,x0要在x附近
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号