单变量微积分笔记8——最值问题和相关变率
寻找最值
在上篇文章曲线构图中,我们可以非常容易地从图上找到函数的最值点。想要求得一个函数的最值点,自然会联想到通过构图寻找,但是构图并不是一个轻松的过程。观察最值点在函数曲线上的位置,可以得出结论:最值点可能存在于临界点、无限远端或驻点。因此仅需要知道这几个点便可以知道函数的最值点。
正方形的最大面积之和
很多情况下最值问题会以文字叙述的形式出现,下面是一个典型的例子:
将一段长为1米的绳子剪成两段,每段围成一个正方形,这两个正方形的最大面积之和是多少?
利用初等代数知识,设其中一段绳长为x米,则另一段是1-x,隐含约束是0 < x < 1
两个正方形的面积之和S = (x/4)2 + ((1 – x)/4)2 = (2x2 – 2x + 1)/16
边界值:当x→0+, S → 1/16; x→1-, s → 1/16
开始寻找驻点。

唯一驻点x0 = 1/2,驻点值S(x0) = 1/32
由于知道S是一个抛物线,所以可以确定驻点值就是最小值;最大值应当在抛物线两端,根据x的定义域,S的极限值是1/16,结合实际就是:其中一段绳子越短,两个正方形的面积之和最大。
盒子的最小表面积
固定容积的无顶盖的盒子,盒子底部是正方形,使其表面积最小是多少?

如上图所示,设盒子的底边x,高为y,则体积V = x2y,表面积S = x2 + 4xy
由于体积固定,将y用x表示,y=V/x2,S = x2 + 4V/x
这里含的条件是 0 < x < +∞,当x→0+, S → +∞; x→+∞, S → +∞
边界值没有指望了,寻求驻点:

有唯一驻点:

表面积的最小值就是3×21/3V2/3
这个表达式太长了。我们注意到在驻点x和y是跟体积有关的定值:

这就是答案,当x/y=2时,表面积最小。
解法2,使用隐函数微分法
V = x2y, S = x2 + 4xy

最短时间
一辆汽车从小路上的某一点开往高速路尽头的工厂,汽车在小路上和高速的速度是30和60。假设小路上处处可走,且能够随意进入高速,如果汽车要在最短时间内到达工厂,应该从哪里进入高速?

首先将其转化成数学模型:

高速路段BE的长度是b,汽车从C点进入高速,问题转换为求最佳的x。A到E的总时间:

当t’ = 0时,耗时最短,此时a2 = 3x2,所以x = 3-1/2a耗时最短。
然而这并不是全部答案,如果x > b,那么直接走直线就是最短的耗时。
相关变率
相关变率是微积分在实际问题中的一类应用,求解的是变化率问题,通常很有趣。在求解最小表面积时,我们最后使用了隐函数微分法求解,使答案直指目标,在相关变率问题中,继续尝试隐函数微分法。
汽车测速
路段的限速为100km/h,交警手持测速设备在距公路垂直距离为30米的地方对过往车辆测速。一辆汽车在该公路上行驶,测速设备探得该汽车现距离交警50米,以80km/h的速度接近交警,该车是否正在超速行驶?
根据题目可以得到下面的模型:

直角三角形的三边都是已知的,一个隐藏的因素是时间t,随着时间的变化,D和x都将发生变化。汽车对于交警的速度相当于距离D对于时间t的导数,汽车在公路上的速度相当于x对于t的导数。可使用隐函数微分法求解:

汽车未超速。
水平面上升速度
圆锥体的底面半径为4m,高为10m,以2m3/sec的速度向圆锥体注水,在高5m处,水平面上升的速度是多少?

首先将题目进行一次转换,将水深5m的图形画出来,但是再次使用圆锥体已经没有多大意义,只需要圆锥的横截面即可。由此可以把图形转化为直角三角形:

一个已知条件是注水速度,速度相当于水量对于时间的导数,要求解的是水平面高度对于时间的导数。
r和h已知,r=2h/5,利用体积公式,通过隐函数微分法:

答案是(1/2π)m/sec
悬挂模型
有一根固定长度的绳子,绳上穿有一个可移动的重物。把绳子两端固定,重物将自然下垂,问题是,重物下垂点是什么?
题目中有两个隐含的常量,绳长和两个端点的位置。这很明显要用到椭圆的知识,当绳子两端都在水平面上时,可以得到下面的几何模型:

△ACB是等腰三角形,AB和AC已知,很容易知道C的位置。
然而实际问题往往不这么简单,AB通常不在水平面上,我们将得到一个倾斜的椭圆:

这下有点难度了。
如果我们把椭圆想象成一个密闭的容器,C点看作一个小钢珠,那么无论怎样倾斜这个椭圆,小钢珠都将滑落到椭圆的最低点,也就是切线为0的点。
现在设C点的坐标为(x, y),C就是椭圆曲线的驻点,约束公式是椭圆曲线的公式,我们又可以使用隐函数微分法了。
这似乎没有问题,但实际操作时会发现,由于椭圆是倾斜的,我们不得不引入一些其他变量,这使得该方法异常麻烦,以至于一开始就放弃了。必须想办法把约束公式转换为更简单的模型:
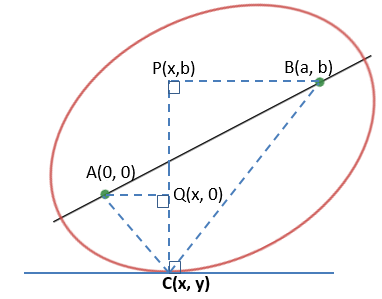
如上图所示,引几条辅助线,形成两个直角三角形,并且PC⊥切线。设A点的坐标是(0,0),B点坐标为(a,b),由此可知P和Q的坐标分别是(x,b),(x,0),QA=x,QC=-y,PC=b-y,PB=a-x;设绳长为L,于是约束公式变成了:

可以使用隐函数微分法了,此处分开计算。
1) 设u=x2+y2,根据链式求导法则:

2) 设u=(a-x)2+(b-y)2,根据链式求导法则:

1)和2)的求导都反复使用了链式求导法则。
3) 结合约束公式:

看上去很复杂,但是由于C点是驻点,所以y’=0,代入上式后:

这就是答案了,它展示了xy与ab的关系,但是太过复杂,严重怀疑在实际应用中是否有价值。
代数上太复杂了,可以看看它的几何意义。
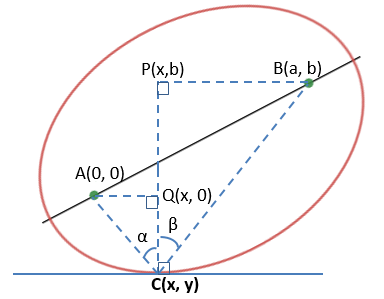
如果把等式代入上图,那么得到下面的结果:

这就是有意义的结果了。
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号