单变量微积分笔记7——曲线构图

 　　曲线构图的目标是根据f’(x)和f’’ (x)画出原函数f(x)的图像。

　　原函数：f(x) = 3x-x³

　　f’(x) = 3-3x²

　　f’’(x) = -6x

函数的凹凸性

　　前提是：设f(x)在[a,b]上连续，在(a,b)内具有一阶和二阶导数。

　　如果函数f’(x) > 0，则f(x)在(a,b)内是递增的；如果f’(x) < 0，则f(x)在(a,b)内是递减的。这很好理解，f’(x)是f(x)在x点切线的斜率，只有函数递增时，切线的斜率才能大于0。

　　如果f’’(x) > 0，则f’递增；如果f’’(x) < 0，则f’递减。这相当于上一条结论的扩展，因为f’’是f’的导函数。

　　凹凸性：

　　（1）若在(a,b)内f’’(x) < 0，则f(x)在(a,b)上的图形是凹的，f’递减，即f的切线斜率递减；

　　（2）若在(a,b)内f’’(x) > 0，则f(x)在(a,b)上的图形是凸的，f’递增，即f的切线斜率递增。

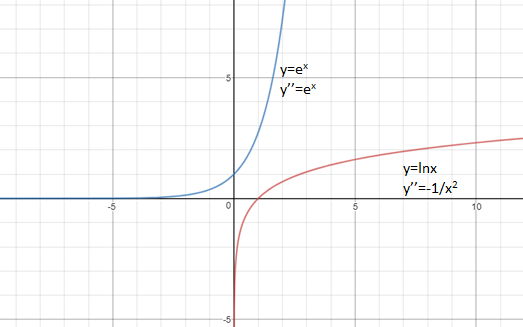
　　上图中y=e^x的二阶导数y’’=e^x > 0，y=e^x是凸的；y=lnx的二阶导数y’’=-1/x²<0，y=lnx是凹的。

　　奇怪的是，国内外的教材对凸凹的定义是不一样的。同济大学的教材中，f’’大于0，函数为凹，f’’小于0，函数为凸，跟上面的定义正好相反。在一些微积分教材中，有将凸称为上凸，凹成为下凸；还有反着叫的……越来越乱了。

极值点和驻点

　　原函数f(x) = 3x-x³

　　f’(x) = 3 - 3x² = 3(1-x²)

　　

　　由此可以画出f(x)的简图：

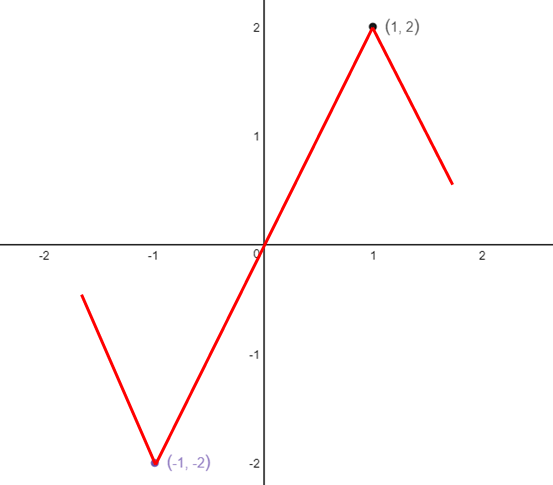
　　(-1, -2)和(1, 2)是两个重要的点，经过这两个点后，f’的符号改变，f的递增递减发生变化，在这两个点上，f’(x)=0，这两个点称为函数的极值点。需要注意的是，极值点不是最值点，仅仅决定了导数的符号改变。

　　当f’(x₀) = 0时，称x₀为驻点，f(x₀)为驻点值。原函数f(x)=3x-x³有±1两个驻点，对应的驻点值为±2。显然，极值点一定是驻点，但驻点不一定是极值点，因为驻点两侧的导数符号可能相同。如下图所示，y=x³的驻点x₀=0，驻点两侧的导数符号相同，函数的增减性未发生变化：

拐点

　　此时，我们已经得到原函数f(x)=3x-x³的两个极值点(1,2)(-1,-2)，再将x=0代入，得到第三个点(0,0)。

　　由于极值点确定了函数增减的改变，又知道f(x)=3x-x³是一个曲线，所以经过极值点的一定是一段弧线，f(x)的简图：

　　

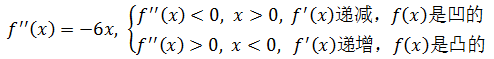
　　由此可知f’’(x₀)=0是原曲线的凹凸分界点，称x₀为f(x)的拐点。

　　有了拐点信息后就可以知道曲线凹凸性，即切线的变化率。

无限远端

　　还有一点无法在有限的二维平面内展现，就是曲线的无限远端，但这并不妨碍我们对其探索。

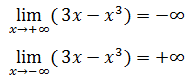
　　由此可知曲线的两端向±∞方向无限延伸。

　　可以根据上述信息构图：

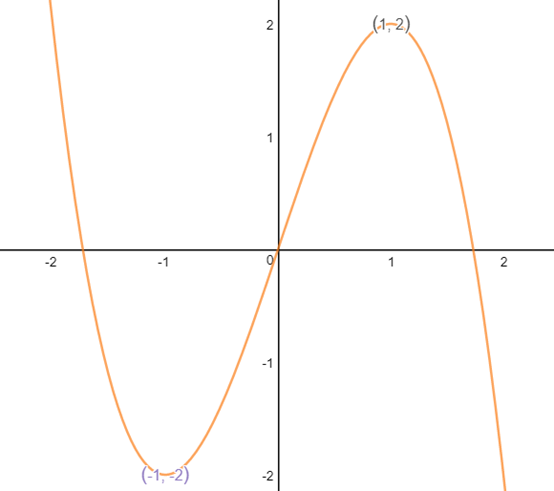
双曲函数构图

　　下面是如何对双曲线f(x) = (x+1)/(x+2)构图。

　　双曲线函数有点特性了，在x=-2处没有定义，所以该函数是在x=-2处断开的。可以得到下面四个极限：

 

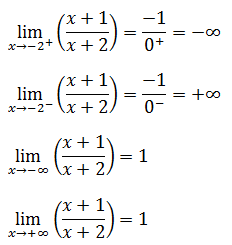
　　根据上面的极限可确定曲线的四个端点，它们都是无限远端，可以画出如下草图：

　　有点丑陋了，这不是我画的最漂亮的图。

　　接下来补充中间缺失的部分，如何确定中间是平滑的？会不会出现波浪形？这些信息需要由驻点确定。

　　f’(x)=1/(x+2)², x≠-2

　　由于f’(x) > 0，所有f(x)在-2的两侧都是递增的；由于f’(x) ≠0，所以f’(x)没有驻点，函数在-2的两侧的增减性不会发生改变。

　　f’’(x) = -2/(x+2)³, x≠-2

　　f’’(x) > 0,  -∞ < x < -2, 函数是凸的

　　f’’(x) < 0,  -2 < x < +∞, 函数是凹的

　　f’’(x) ≠ 0, 函数没有拐点

　　二阶导数确定了曲线的弧度方向。

　　至此可以构图：

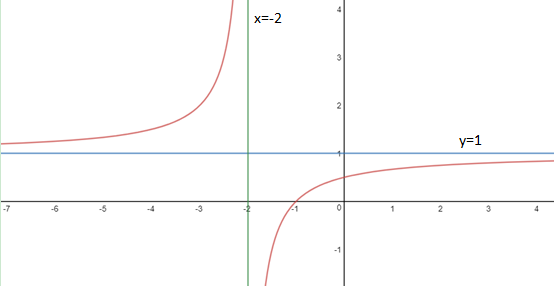
构图的一般步骤

　　构图的一般步骤：

1. 描点，找出函数中奇点，即函数未定义的点
2. 标出无限远端
3. 标出驻点，即f’(x)=0的点；判断f’(x)在每个驻点或不连续点为端点的区间内的符号，由此判断函数的递增和递减性
4. 观察二阶导数f’’的正负性，以便判断f(x)的凹凸，f’’(x)=0是拐点
5. 组合1~4构图

示例

　　f(x) = x/lnx

　　按照上节的步骤构图。

　　1.找出奇点

　　当x=1是，lnx=0，f(x)无意义，奇点是x=1；由于使用了对数lnx，隐含的条件是x>0，所以可以得到下面两个极限：

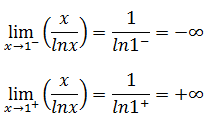
　　此外，还可以知道f(0) = 0

　　2.标出无限远端

　　由于x的定义域是(0, +∞)且x≠1，所以x只能从正向趋近于0；由于lnx是x的高阶无穷小，所以第二个极限是+∞。目前的草图：

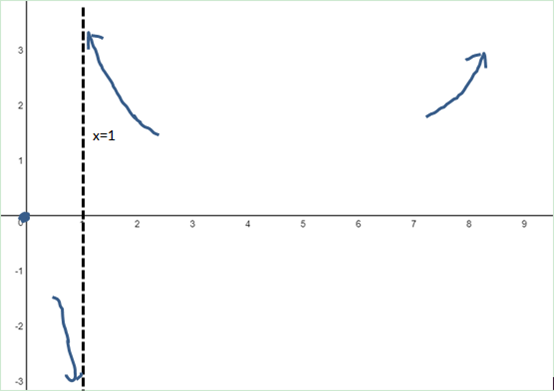
　　几乎可以断定剩余的部分的样子。

　　3.找出驻点，判断函数的递增和递减

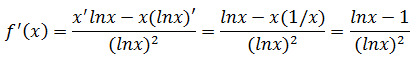
　　f’(x) = 0，则x=e，f(e) = e/lne = e，仅有一个驻点

　　f’(x) < 0,  0 < x<1, 1< x < e，函数递减；

　　f’(x) > 0,  e < x，函数递增

　　代入一些简单值作为修饰后就可以作图了，可以省略求二阶导数，图像不会差太多。本例还是继续计算二阶导数。

　　4.观察二阶导数f’’的正负性，以便判断f(x)的凹凸

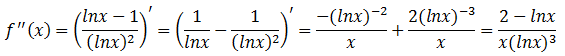
　　f’’(x) < 0, 0 < x <1, 函数是凹的

　　f’’(x) > 0, 1 < x < e², 函数是凸的

　　f’’(x) < 0, e² < x, 函数是凹的

　　f’’(x) = 0, x = e², 拐点是e²

　　至此，可以构图了：

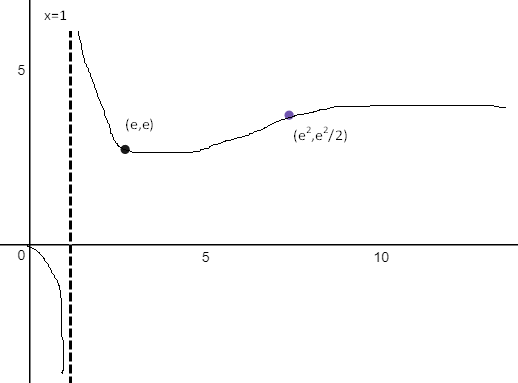
构图结果

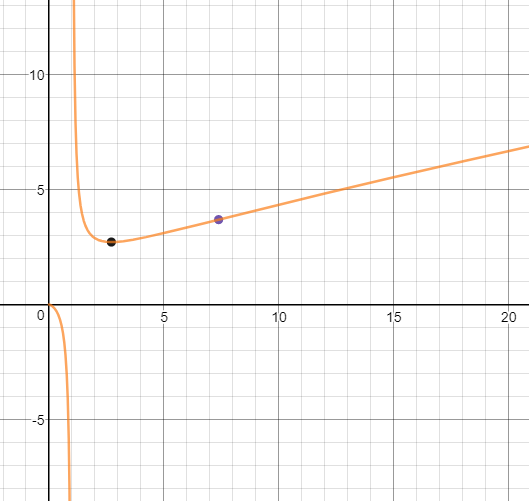
真实图像

总结

1. 若在(a,b)内f’’(x) < 0，则f(x)在(a,b)上的图形是凹的，f’递减
2. 若在(a,b)内f’’(x) > 0，则f(x)在(a,b)上的图形是凸的，f’递增
3. 极值点，经过极值点后f’(x)的符号改变
4. 驻点f’(x₀)=0，x₀是驻点，f(x₀)是驻点值
5. 拐点，经过拐点后，函数的凹凸性发生改变
6. 利用构图的一般步骤为双曲线构图

 

---

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”