使用Apriori进行关联分析（二）

　　书接上文（），介绍如何挖掘关联规则。

发现关联规则

　　我们的目标是通过频繁项集挖掘到隐藏的关联规则。

　　所谓关联规则，指通过某个元素集推导出另一个元素集。比如有一个频繁项集{底板,胶皮,胶水}，那么一个可能的关联规则是{底板,胶皮}→{胶水}，即如果客户购买了底板和胶皮，则该客户有较大概率购买胶水。这个频繁项集可以推导出6个关联规则：

　　{底板,胶水}→{胶皮},

　　{底板,胶皮}→{胶水},

　　{胶皮,胶水}→{底板},

　　{底板}→{胶水, 胶皮},

　　{胶水}→{底板, 胶皮},

　　{胶皮}→{底板, 胶水}

　　箭头左边的集合称为“前件”，右边集合称为“后件”，根据前件会有较大概率推导出后件，这个概率就是之前提到的置信度。需要注意的是，如果A→B成立，B→A不一定成立。

　　一个具有N个元素的频繁项集，共有M个可能的关联规则：

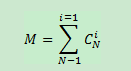
　　下图是一个频繁4项集的所有关联规则网格示意图，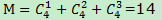 

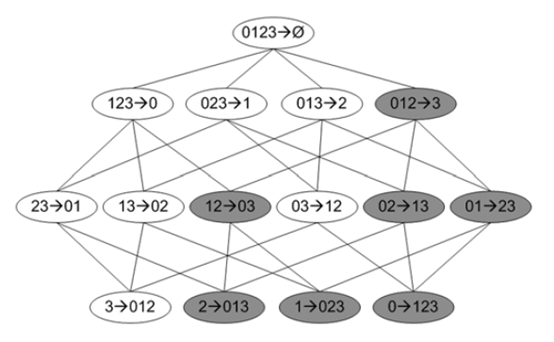
　　上图中深色区域表示低可信度规则，如果012→3是一条低可信度规则，则所有其它3为后件的规则都是低可信度。这需要从可信度的概念去理解，Confidence(012→3) = P(3|0,1,2)，Confidence(01→23)=P(2,3|0,1)，P(3|0,1,2) >= P(2,3|0,1)。由此可以对关联规则做剪枝处理。

　　还是以上篇的超市交易数据为例，我们发现了如下的频繁项集：

　　对于寻找关联规则来说，频繁1项集L1没有用处，因为L1中的每个集合仅有一个数据项，至少有两个数据项才能生成A→B这样的关联规则。

　　当最小置信度取0.5时，L2最终能够挖掘出9条关联规则：

　　从频繁3项集开始，挖掘的过程就较为复杂。

　　假设有一个频繁4项集（这是杜撰的，文中的数据不能生成L4），其挖掘过程如下：

　　因为书中的代码假设购买商品是有顺序的，所以在生成3后件时，{P2,P4}和{P3,P4}并不能生成{P2,P23,P4}，如果想去掉假设，需要使用上篇中改进后的代码。

　　发掘关联规则的代码如下：

 1 #生成关联规则
 2 #L: 频繁项集列表
 3 #supportData: 包含频繁项集支持数据的字典
 4 #minConf 最小置信度
 5 def generateRules(L, supportData, minConf=0.7):
 6     #包含置信度的规则列表
 7     bigRuleList = []
 8     #从频繁二项集开始遍历
 9     for i in range(1, len(L)):
10         for freqSet in L[i]:
11             H1 = [frozenset([item]) for item in freqSet]
12             if (i > 1):
13                 rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
14             else:
15                 calcConf(freqSet, H1, supportData, bigRuleList, minConf)
16     return bigRuleList
17 
18 
19 # 计算是否满足最小可信度
20 def calcConf(freqSet, H, supportData, brl, minConf=0.7):
21     prunedH = []
22     #用每个conseq作为后件
23     for conseq in H:
24         # 计算置信度
25         conf = supportData[freqSet] / supportData[freqSet - conseq]
26         if conf >= minConf:
27             print(freqSet - conseq, '-->', conseq, 'conf:', conf)
28             # 元组中的三个元素：前件、后件、置信度
29             brl.append((freqSet - conseq, conseq, conf))
30             prunedH.append(conseq)
31 
32     #返回后件列表
33     return prunedH
34 
35 
36 # 对规则进行评估
37 def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
38     m = len(H[0])
39     if (len(freqSet) > (m + 1)):
40         Hmp1 = aprioriGen(H, m + 1)
41        # print(1,H, Hmp1)
42         Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
43         if (len(Hmp1) > 0):
44             rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)

 

　　由此可以看到，apriori算法需要经常扫描全表，效率并不算高。

 

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”

posted on 2017-08-29 22:32  我是8位的  阅读(4455)  评论(1)  编辑  收藏  举报

导航