单变量微积分笔记4——导数4（反函数的导数）
什么是反函数
一般地，设函数y=f(x)(x∈A)的值域是C，若找得到一个函数g(y)在每一处g(y)都等于x，这样的函数x= g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数，记作y=f-1(x) 。反函数y=f-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域。最具有代表性的反函数就是对数函数与指数函数。
例1：y=2x-1的反函数是y=0.5x+0.5
y=2x的反函数是y=log2x
例2：求函数3x-2的反函数
y=3x-2的定义域为R,值域为R.
由y=3x-2解得
x=1/3(y+2)
将x,y互换,则所求y=3x-2的反函数是y=1/3(x+2)
反函数的性质
这个厉害了，反函数一般具有以下几种性质：
1、互为反函数的两个函数的图象关于直线y=x对称；
2、函数存在反函数的充要条件是，函数在它的定义域上是单调的；
3、一个函数与它的反函数在相应区间上单调性一致；
4、偶函数一定不存在反函数，奇函数不一定存在反函数。若一个奇函数存在反函数，则它的反函数也是奇函数。
5、一段连续的函数的单调性在对应区间内具有一致性；
6、严格增（减）的函数一定有严格增（减）的反函数【反函数存在定理】。
7、反函数是相互的
8、定义域、值域相反对应法则互逆
9、不是所有函数都有反函数如y=x的偶次方（不满足第2条如y=x2在x<=0时是递减的，在x>=0时是递增的）
10、反函数的导数关系：如果X=F(Y）在区间I上单调，可导，且F‘（Y）不等于0，那么他的反函数Y=F’（X）在区间S={X|X=F(Y),Y属于I}内也可导，且[F‘（X)]'=1\[F’（Y）]'。
反函数求导
用隐函数微分法可以求导任意反函数，只要我们知道原函数的导数。
示例1：(tan-1x)’
y = tan-1x = arctanx，定义域是(-π/2, π/2)，值域是(-∞,+∞)，原函数是tany = x
先来看图形，中间的红色曲线是定义域是(-π/2, π/2)时tanx的曲线，蓝色曲线是其对应的反函数y = arctanx
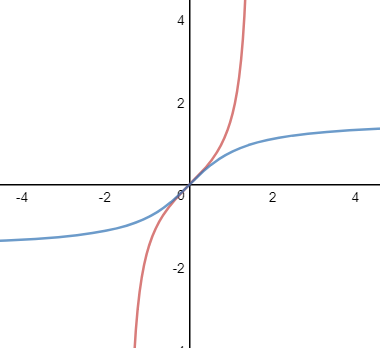
以下是y = tan-1x求导过程：
上式等价于tany=x，求导等价于对tany=x求导。对隐函数tany=x两侧同时求导：
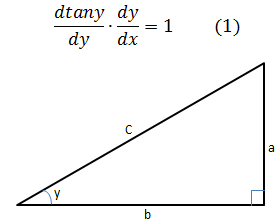
在上图直角三角形中，tany=a/b，siny=a/c，cosy=b/c，由此，tany=siny/cosy。代入（1）：
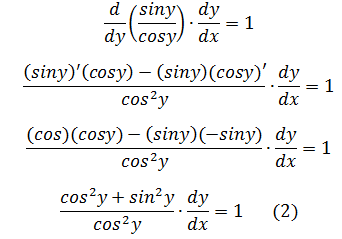
在上图直角三角形中，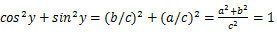
，代入（2）：
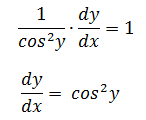
y是x的函数，我们需要将y替换成x，如果直接替换，将得到cos2(tan-1x)，可以对其化简，但这很繁琐，所以还是回到直角三角形中考虑使用更简单化简的方法。
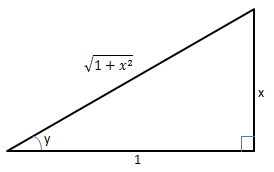
由于tany=x，所以将直角三角形中的两个直角边分别设为x和1，这样就可以求得斜边，由此可以计算cosy：
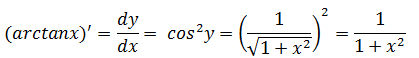
示例2：(sin-1x)’
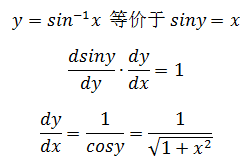
出处：微信公众号 "我是8位的"
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
