单变量微积分笔记3——导数3（隐函数的导数）

幂函数的扩展形式

　　f(x) = xⁿ的导数：f’(x) = nx^n-1，n是整数，该公式对f(x) = x^m/n, m,n 是整数同样适用。

　　推导过程：

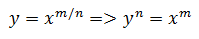
　　两端同时求导，由于y是x的函数，根据链式求导法则：

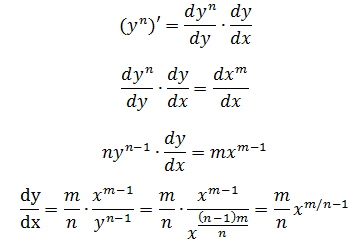
什么是隐函数

　　引自知乎：

　　“如果方程F(x,y)=0能确定y是x的函数，那么称这种方式表示的函数是隐函数。

　　“本质上F(x,y)=0函数y=f(x)是一样的，但是在数学理论中，总有一些函数，人们已经证明它们的函数关系，但是还是无法表示成显函数的形式，就叫做隐函数。隐函数一般是一个含x,y的方程如e^y+x^2+x=0这种形式，由于形式复杂，y不容易变形为用含x的式子表示，即不易表示为y=f(x)，但如果能确定对于x的每一取值，y都有唯一确定的值与它对应的话，y就是x的函数关系，但这样的关系隐含在方程中，不容易写成明显的函数关系的形式，所以称隐函数。”

示例1：x² + y² = 1求导

　　对x² + y² = 1，y >= 0求导

　　解法1：y = (1-x²)^1/2

　　根据链式求导法则，

 

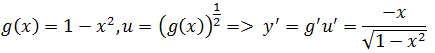
　　解法2：y² = 1 – x²，y是x的函数，等式两边同时求导：

　　解法3：隐函数保持不变，直接对等式两侧求导：

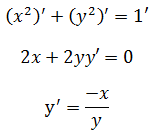
示例2：y⁴ + xy² – 2 = 0求导

　　用显示求导方法将麻烦到一定程度，所以直接使用隐示求导：

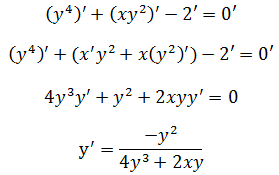
　　到此，隐示法求解的结果还是隐示，但似乎没有必要再把y用x替换，当需要求解f(x,y)=y⁴+xy²-2=0在某一点(x₀,y₀)的导数时，只需要将x₀,y₀代入即可；如果只给出x₀，也可以通过简单的代入法求出对应的y₀，再代入隐示结果。

 

---

　　 出处：微信公众号 "我是8位的"

 　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　 扫描二维码关注作者公众号“我是8位的”