概率统计21——指数分布和无记忆性
指数分布(Exponential distribution)是一种连续型概率分布,可以用来表示独立随机事件发生的时间间隔的概率,比如婴儿出生的时间间隔、旅客进入机场的时间间隔、打进客服中心电话的时间间隔、系统出现bug的时间间隔等等。
指数分布的由来
指数分布与泊松分布存在着联系,它实际上可以由泊松分布推导而来。
泊松分布(概率统计15)中已经介绍过泊松分布,除了作为二项分布的近似外,当独立事件发生的频率固定时,泊松分布还可以刻画算单位时间内事件发生次数的概率分布。
假设某个公司有一个带伤上线的系统,每周平均的故障次数是2次,在下周不发生故障概率是多少?
每周平均的故障次数是2次,我们可以把“一周”看作单位时间,程序的故障率是λ=2,单位时间内发生故障的次数X符合泊松分布X~Po(λ)。在下周不发生故障的概率相当于发生了0个故障的概率:
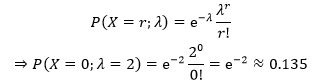
现在要求计算两周之内不发生故障的概率。我们用随机变量T>2表示在2个单位时间内系统未发生故障的事件。在已知下周不发生故障的概率的情况下,P(T>2)计算起来很容易:

我们换一种思路。之前是把“一周”看作单位时间,单位时间内事件发生的频率是λ=2。现在是变成了双倍的单位时间,故障发生的频率自然就变成2λ=4,这样一来,两周之内不发生故障的概率是:

结果和①相等。
时间是连续的,如果计算T=1.5周内不发生故障的概率,①就显得无能为力了。但是②却没有任何问题,只要把单位时间内事件的频率λ随着时间T进行放缩就可以了:

将问题推广到任意时间间隔:

反过来,故障在时间 t 之内发生的概率就是1-P(T>t):
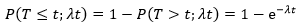
现在把T换成X:
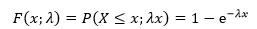
这里的F(x;λ)就是指数分布的分布函数,λ表示平均每单位时间内事件发生的次数,随机变量X表示时间间隔。
F(x;λ)对应的密度函数是:
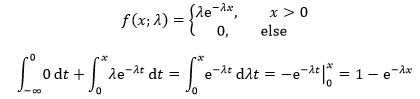
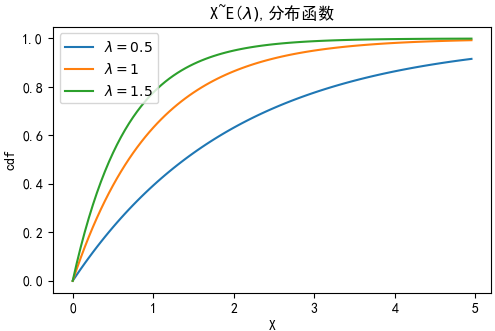
随机变量X符合参数为λ>0的指数分布,记作X~E(λ)。
有些资料的写法是:

仅仅是用θ代替了1/λ。

无记忆性
指数分布的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。如果一个随机变量呈指数分布X~E(λ),当s, t ≥0时:
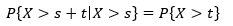
先来看看这个等式为什么成立。

因此二者相等。
在前面的推导中可以看到:
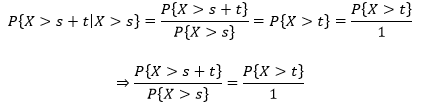
累积概率对应面积,这个结论告诉我们,在指数分布下,P{X>s+t}和P{X>s}对应的面积的比值等于P{X>t}对应的面积和总体面积的比值:
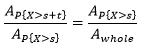
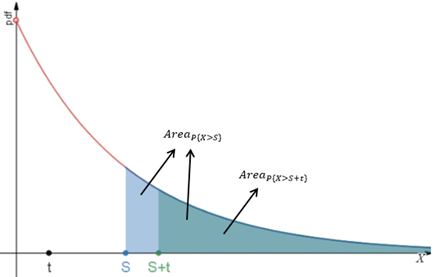
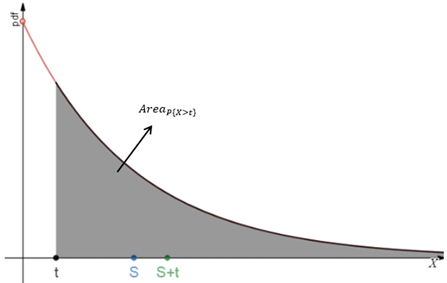
理解无记忆性
我们已经知道指数分布可以用来表示独立随机事件发生的时间间隔的概率分布,在精密元件的可靠性研究中,指数分布通常用于描述对元件发生缺陷数测量结果。但是无记忆性又指出,元件在经过s时间的工作之后,它的寿命分布与原来还未工作时的寿命分布相同。这就好比有一个已经用了10年的灯泡和一个刚买的灯泡,现在我告诉你它俩在未来一年里报废的概率相同,你信吗?
一个著名的问题是“赌徒心理”。假设在赌桌上只能押大或小,某个赌徒已经连续押了10次小,但都输了,于是赌徒认为,下次再出现小的可能性非常低,于是他想把兜里的钱全部押大,试图翻本。

不妨帮助赌徒分析一下翻本的概率。
假设这是一个公平的赌场,大和小的概率都是0.5,用随机变量X表示第一次出现“大”时所参与的赌局数,X符合几何分布:

其中p表示出现“大”的概率,q表示出现“小”的概率。直到第11次才出现“大”的概率是0.511,这是个非常小的数值,可见这个赌徒确实运气不佳。
接着分析,用X>10表示连续10次以上没出现“大”的事件,以此为前提,下一次(第11次)出现大的概率是:
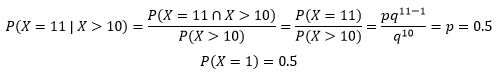
在连续押小输掉10次的条件下,下一次出现“大”,和第1次就出现“大”的概率相同。对于赌徒来说,每一局都是全新的,下一次赢钱的概率和之前的输赢没有任何关系,这就是所谓的无记忆性。
指数分布与几何分布类似,只不过把离散随型机变量变成了连续型。
实际上生活中有很多无记忆性的例子,比如车牌摇号。对于参与摇号的人来说,在每一次摇号中摇中的概率都是相等的。有人说不对啊,明明告诉我摇中的概率是1%,100次里面怎么还不能中一回吗?所谓的1%摇中率,是在大数定律下才起作用,而现实生活中我们面对的往往是“小数”。可以用程序模拟一下:
1 import numpy as np 2 3 np.random.seed(41) 4 for i in range(1, 11, 1): 5 m = 100 * i # 试验次数 6 nums = np.random.randint(1, 101, 200) # 从1~100中随机选择m个数字 7 p_50_size = nums[nums == 50].size # m个数字中出现50的次数 8 print('一共参与摇号{}次,摇中{}次,概率{}'.format(m, p_50_size, p_50_size/m))
结果显示:
一共参与100次摇号,摇中0次,概率0.0
一共参与200次摇号,摇中0次,概率0.0
一共参与300次摇号,摇中3次,概率0.01
一共参与400次摇号,摇中3次,概率0.0075
一共参与500次摇号,摇中2次,概率0.004
一共参与600次摇号,摇中3次,概率0.005
一共参与700次摇号,摇中4次,概率0.005714285714285714
一共参与800次摇号,摇中3次,概率0.00375
一共参与900次摇号,摇中3次,概率0.0033333333333333335
一共参与1000次摇号,摇中5次,概率0.005
每月摇号一次,一个人穷尽一生也满足不了“大数”,摇号还真是件没谱的事。
因为无记忆性的关系,有人戏称服从指数分布的随机变量就像传说中金鱼只有7秒钟记忆一样,是“永远年轻的”。也正是这一点限制了指数分布的应用,因为指数分布忽略了损耗。但是,指数分布仍然可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型,特别是在部件或机器的整机试验中得到广泛的应用。

至于灯泡的寿命是否符合指数分布,其实我也不知道。也许现在制作工艺提升了,灯泡已经是具有高可靠性的产品,灯泡明天是否还能正常工作,完全取决于是否遭到了外力的破坏,日常损耗所起到的作用可以忽略不计,这种情况下,灯泡的使用寿命才有可能符合指数分布。
关于保修期的问题
冰箱平均10年出现一次大的故障,求:
(1)冰箱使用15年后还没有出现大故障的比例。
(2)如果厂家想提供大故障免费维修的质保,试确定保修1~5年内,需要维修的冰箱的占比。
冰箱平均10年出现大的故障,可见故障率不高,可以认为故障次数服从泊松分布,单位时间是1年,λ=0.1。
(1)根据指数分布:
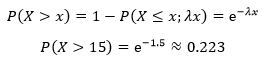
冰箱使用15年后还没有出现大故障的比例约等于22.3%。
(2)
1 from scipy import stats 2 3 lam = 0.1 4 for i in range(1, 6): 5 print(stats.expon.cdf(i, scale=1/lam))
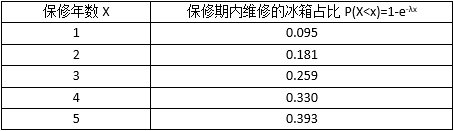
上表告诉了我们冰箱的保修期一般都是2年以内的原因,厂家为了把上门修理的次数控制在20%以内,一般选择保修2年。
期望和方差
对于X~E(λ)的指数分布来说,它的期望是1/λ,方差是1/λ2。
先来看期望:

根据分部积分:

再来看方差:
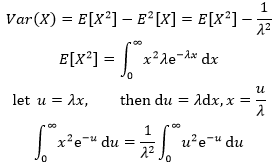
继续利用分部积分:
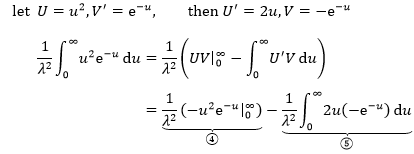
将u=λx代入④:
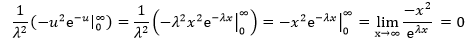
将在E[X]中求得的③代入⑤中:
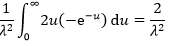
最终:
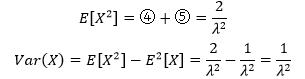
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号