伽玛函数
伽玛函数(Gamma函数),也叫欧拉第二积分,是阶乘函数在实数与复数上扩展的一类函数。伽玛函数在分析学、概率论、偏微分方程和组合数学中有重要的应用。
我们通常看到的伽玛函数是这样的:

这到底是个什么东西?有什么用?欧拉又是怎么发现它的?

欧拉大神
伽玛函数的起因
发现伽玛函数的起因是数列插值。数列插值问题,通俗地说就是把数列的通项公式从整数定义域扩展到实数。例如数列1,4,9,16,.....可以用通项公式n²表达,即便n为实数的时候,这个通项公式也是良好定义的。直观的说,就是可以找到一条平滑的曲线y = x²,该曲线能够通过所有的整数点(x, x²),从而可以把定义在整数域的公式扩展到实数域。
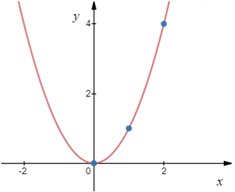
1728年,哥德巴赫开始处理阶乘序列的插值问题:1,2,6,24,120,720,...,既然可以计算2!, 3!,…,是否可以计算2.5!呢?把最初的一些(n, n!)的点画在坐标轴上,确实可以看到,能够画出一条通过这些点的平滑曲线。问题是,这条曲线是什么?

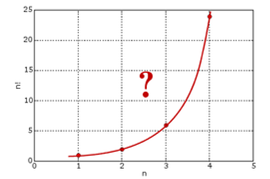
哥德巴赫无法解决阶乘往实数域上扩展的这个问题,于是写信请教尼古拉斯·贝努利和丹尼尔·贝努利两兄弟,由于欧拉当时正好和丹尼尔·贝努利在一块玩,他也因此得知了这个问题。之后欧拉于1729年完美地解决了这个问题,由此导致了伽玛函数的诞生。当时欧拉只有 22 岁,这让我感觉自己就是混吃等死的。
发现伽玛函数
在某一个特殊的时刻,欧拉发现阶乘n!可以用一个无穷乘积表示:

如果有m项乘积:
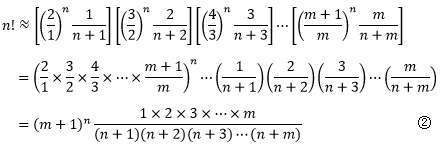
当m远远大于n时,上式可继续计算:
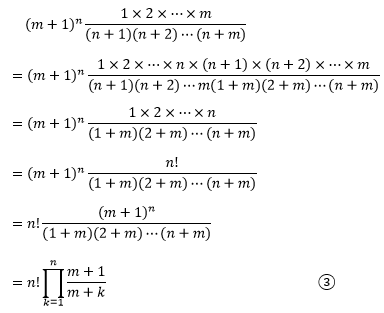
当m→∞时,无穷乘积的极限:
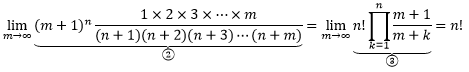
很难想像在没有计算机的年代能够发现这个变态的无穷乘积,估计欧拉当年是根据极限倒推无穷乘积,然后对外宣称在机缘巧合下发现了无穷乘积。
值得注意的是,n!明显不等于③,③又是由②整理而来的,因此n!也不等于②,而是在m→∞时n!等于②或③的极限。以n = 2为例,n! = 2,m是2、50、100时,②的结果分别是1.5、1.9615384615384617、1.980392156862745,展开的越多,越接近于n!。
有了这个无穷乘积,欧拉便开用1/2代入①进行尝试:

根号里面的东西是英国数学家沃利斯(John Wallis)在1665年写下的沃利斯公式:

于是欧拉把沃利斯公式折半:
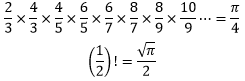
π真是一个神奇的数字!
1665年牛顿还很小,还没有发明积分,沃利斯用各种巧妙的技巧得到了这个结论,推导过程实际上是在处理 。受沃利斯的启发,欧拉开始考虑如下的一般形式的积分:
。受沃利斯的启发,欧拉开始考虑如下的一般形式的积分:

此处n为正整数,a为正实数。利用分部积分:
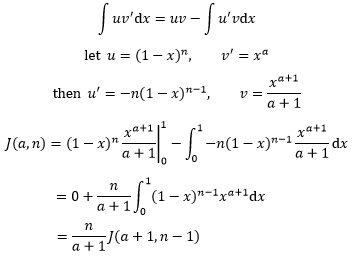
继续使用分部积分:
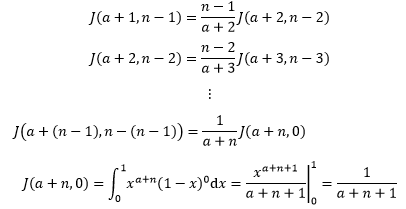
上面所有递推合并到一起就得到了最终的结果:

现在阶乘变成了积分的形式。然而这个式子的前提是n是正整数,无法推广到分数,欧拉继续研究如何化简这个表达式。a是一个任意实数,能否让a消失?一个惯用的方法是取极端值,a > 0的一个极端是无穷,看看让a趋近于无穷时会得到什么结果。这里欧拉使用的技巧是让a等于两个实数的商:
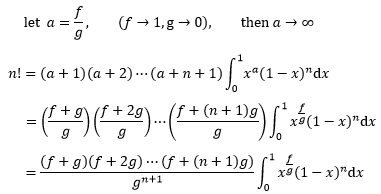
等式两侧同时除以(f+g)(f+2g)…(f+ng):
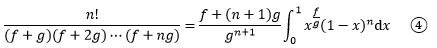
当f→1,g→0时,左侧趋近于n!,但是右侧出现了讨厌的0分母,此时为了简化计算:
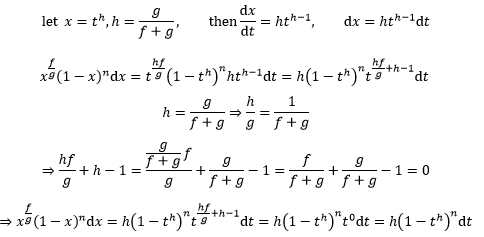
将上式结论代入④:
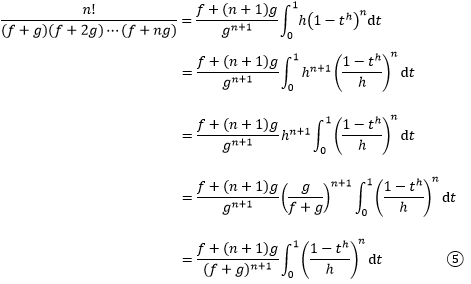
用求极限的方式去掉f和g:
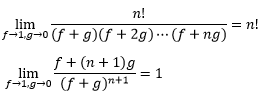
当f→1,g→0时h→0,(1-th)/h的极限变成了0/0的形式,在洛必达法则的帮助下,0/0形和∞/∞形的极限也是可以求解的。令u(h) = 1-th,v(h) = h,根据洛必达法则:
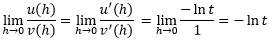
于是在对⑤的等式两侧求极限时,神奇的一幕出现了:
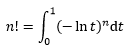
任意实数a已经消失了,n!变成了一个简洁的积分形式。继续变换:

这就是欧拉最早定义的伽玛函数,实际上就是阶乘扩展到实数范围:
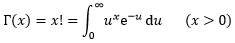
但是欧拉后来修改了伽玛函数的定义,变成了:
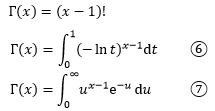
这也是现在我们所说的伽玛函数,⑥和⑦是两种表达,⑦更为常见,从积分域可以看出t和u的取值范围。
伽玛函数的性质
欧拉在伽玛函数的推导中实际上引入了两类积分形式:
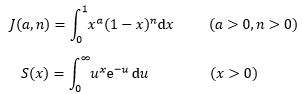
后来这两个积分的参数做了-1的偏移,改为:
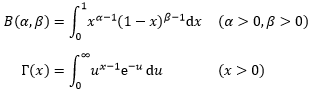
B(α, β)现在成为贝塔函数或贝塔积分,Γ(x)实际上是在计算x – 1的阶乘,两个函数之间存在一些很好的关系:
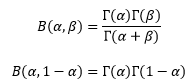
我们知道0! = 1,Γ(1)对此进行了解释:

来看一下Γ函数的曲线:
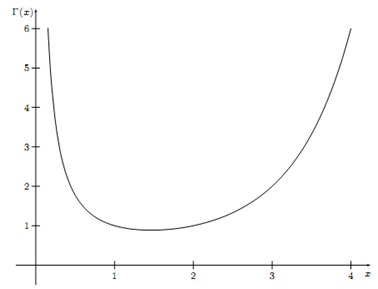
从Γ函数的曲线可以看出Γ函数是一个凸函数,logΓ也是一个凸函数:
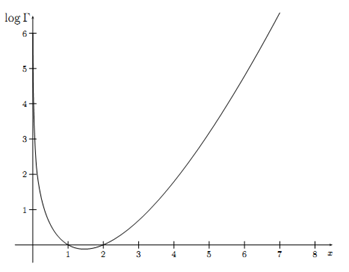
下面的的matlib代码绘制了Γ(x)和logΓ(x)的曲线:
x = 0:0.1:10; plot(x, gamma(x)); axis([0,4,0,6]); xlabel('x'); ylabel('r(x)'); figure; plot(x, lgamma(x)); axis([0,8,-1,6]); xlabel('x'); ylabel('logr(x)');
伽玛分布
伽玛函数在概率统计中频繁现身,泊松分布、贝塔分布、狄克雷分布中都有伽玛函数的身影。当然,发生最直接联系的概率分布是直接由伽玛函数变换得到的伽玛分布。
为了便于看清伽玛分布,先把伽玛函数中的变量名称修改一下:
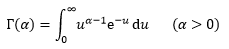
等式两侧同时除以Γ(α):
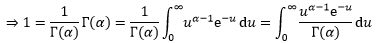
这正好符合连续型概率分布的定义,被积函数就是伽玛分布的密度函数:

如果令u = βx,则:

于是我们得到了伽玛分布的一般形态:
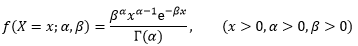
其中α称为形状参数(shape parameter),决定了分布曲线的形状;β称为速率参数(rate parameter)或逆尺参数(inverse scale parameter),决定了曲线的陡峭程度:
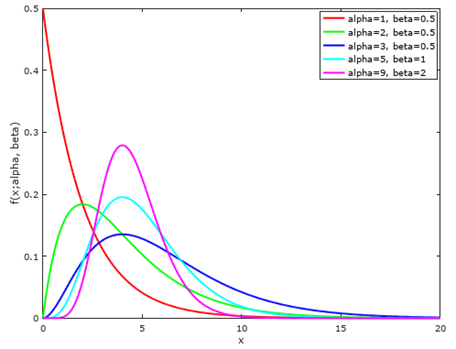
可以看到, β之所以被称为逆尺参数,是因为1/β越大,曲线越陡峭。在matlab中,gamma分布的参数使用的是1/β:
x = 0:0.1:20;
a = [1 2 3 5 9];
b = [0.5 0.5 0.5 1 2];
L(1, 1) = {''};
for i = 1:size(a)(2)
g = gampdf(x, a(i), 1/b(i));
L(1, i) = ['alpha=', num2str(a(i)), ',beta=', num2str(b(i))];
plot(x, g, 'LineWidth',2);
hold on;
endfor
legend(L);
xlabel('x');
ylabel('f(x;alpha, beta)');
axis([0,20,0,0.5]);
概率统计中的众多分布都和Gamma分布有密切关系。以泊松分布为例,随机变量X服从参数为λ的泊松分布分布X~Po(X; λ),其质量函数是:
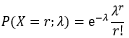
在Gamma分布的密度中取α=r+1,β=1得到:

因此当β=1时,Gamma分布和泊松分布在形式上是完全一致的,只是泊松分布是离散的,而Gamma分布是连续的,可以直观地认为Gamma分布是泊松分布在正实数集上的连续化版本。
伽玛分布的期望值和方差分别为:

本文参考:https://cosx.org/2013/01/lda-math-gamma-function
出处:微信公众号 "我是8位的"
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号