线性代数笔记33——基变换和图像压缩

 

　　原文 | https://mp.weixin.qq.com/s/TXbcQoXw2HGkP3tnvKEpMQ

　　基变换的一个重要应用是压缩，图像、视频、音频和其它一些数据都会因为基变换而得到更高效的压缩存储。线性变换可以脱离坐标系，而描述线性变换的矩阵却要依赖于坐标系，因此选择合适的基会更便于计算。

图像的知识

灰度图像

　　由于景物各点的颜色及亮度不同，摄成的黑白照片上或电视重现的黑白图像上各点呈现不同程度的灰色。把白色与黑色之间按对数关系分成若干级，称为“灰度等级”。范围一般从0到255，白色为255，黑色为0，故黑白图片也称灰度图像，在医学、图像识别领域有很广泛的用途。

　　灰度使用黑色调表示物体，即用黑色为基准色，用不同饱和度的黑色来显示图像。每个灰度对象都具有从 0%（白色）到100%（黑色）的亮度值，下图中每个方块都代表了一个不同的亮度值：

　　我们通常讲的“黑白照片”是一种灰度图像，它与计算机领域中的黑白照片不同，在计算机图像领域中黑白图像只有黑和白两种颜色，而灰度图像在黑色与白色之间还有许多级的颜色深度：

图像存储

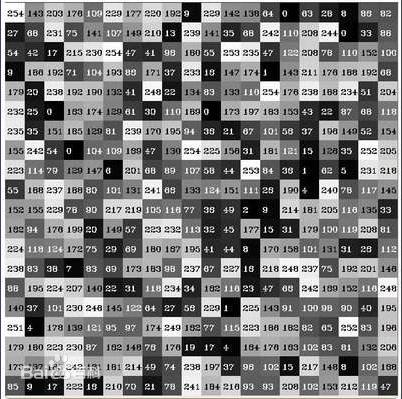
　　考虑一副515×512像素的灰度静态图像，它有2⁸×2⁸个像素，每个像素的灰度值是从0到255，用8bit空间存储。可以用矩阵存储数字图像，每个元素都是一个像素点：

　　我们也可以将一幅图像当成一个有515×512个分量的向量：

　　v是一个R^512×512空间的向量，它的前512个分量是A的第一列，第二个512个分量是A的第二列。这样一来，一个图像就可以看作是一个向量（这里的意思是，在计算时，把一个二维数组转换成一维数组处理，但存储上未必使用一维数组）。如果图像是彩色的，那么每个像素点都需要存储三个数据（RGB），存储空间将是灰度图像的三倍。

图像压缩

　　存储图像将会占据大量的空间，如果不进行压缩，势必会影响系统的加载或网络传输效率。一种标准的图像压缩方式是JPEG（联合图像专家组，Join Photographic Experts Group），JPEG文件的扩展名为.jpg或.jpeg，它用有损压缩方式去除冗余的图像和彩色数据，在获得极高的压缩率的同时能展现十分丰富生动的图像，即可以用较少的磁盘空间得到较好的图片质量。

　　现在有一个512×512灰度图像，图像的某一列像素可能是这样的数值：

　　可以用Pillow查看图像的某一列：

from PIL import Image

img = Image.open('cat.jpg')
width, height = img.width, img.height
px = img.load()
for i in range(height):
    print(px[0, i])

img_gray = img.convert('L') # 灰度图像转换
px = img_gray.load()
for i in range(height):
    print(px[0, i])
img_gray.show()

　　换成彩色图像也一样，只不过向量的每个元素都变成了一个三元组，这里我们还是以简单的灰度图像为例。假设我们用一个向量存储这个灰度图像。在图像压缩前，采用的是向量的标准基，图像是这这些标准基的线性组合：

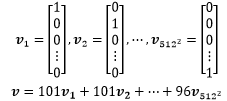
　　对于一个图像来说，相邻像素经常代表同一块区域，比如猫咪的身体，因此灰度值是非常接近的甚至完全相同的。在一个极端情况下，比如图像展示了一块干净的黑板，此时图像的所有像素都相同，如果仍然使用标准基，则完全忽略了图像的这一特性，此时一个更好的基是元素全为1的向量，仅通过这一个基向量就能完整地给出所有像素一致的图像的信息。虽然在大多数实际情况下图像的像素不是一致的，但这种处理思路仍然给了我们压缩的可能。实际上我们经常用全1向量作为图像的一个基向量，问题是，应该选择哪些向量与它配合？

　　下面是几个常用的基向量：

　　±1交叉出现，可以处理黑白交叉的图像，比如一个国际象棋的棋盘：

　　一半是1，另一半是-1，可以处理一半明一半暗的图像，比如日出和日落：

　　这些基向量应该怎样选择呢？不同行业的人员有不同的选择，比如电视行业的人员基于信号扫描的方式选择基，电影行业的人员喜欢另一种，而对于JPEG来说，使用的是傅立叶基。

傅立叶基

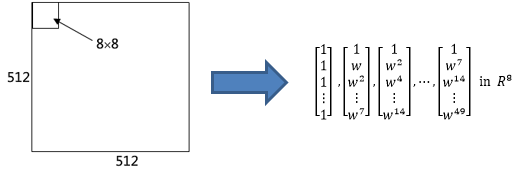
　　傅立叶基包括全1向量，电气工程师称之为DC向量。JPEG将一个图像分解成多个8×8的块，每个块中的64个像素又被拆分成8个8×1的小块，对每一个小块进行基变换处理。

　　实际上这组傅里叶基就是傅立叶矩阵的列向量：

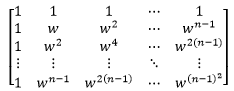
　　这里我们不过多地介绍傅立叶向量，只介绍JPEG压缩图像的原理。每一个8×8的块有64个像素，这些像素可以存储在一个64维向量中，这个向量有64个基向量，因此每一个块都可以看作64个基向量的系数。

　　JPEG的压缩是在64维空间中利用傅立叶向量做基变换。对于每个8×8的块来说，需要进行64次基变换，得到64个新系数。

　　首先输入信号p（8×8的像素块，实际上被拆分成8个8×1的列向量），然后从标准基进行基变换，变成傅立叶基，从而得到新的系数c，这一步是无损的过程。接下来将进行压缩，在压缩过程中将丢失一些信息，是有损过程。通过设置阈值进行压缩，超过阈值的认为是肉眼看不出区别的，即使丢掉也没有太大关系。通过这种方法丢掉一部分基向量，得到一套新的系数 ，用新的系数乘以相应的傅立叶基并求和得到新的向量。

　　最终用于求和的向量已经不是64个，而是去掉了丢掉的部分，可能只剩下两三个，这就是压缩。如果向量个数从64个减到了3个，压缩比率是21:1。

　　视频文件可以看作一幅幅静态图像，压缩每一幅，然后播放，但这不是一个好方法，因为没有利用好视频的性质。视频是一系列连续的、高度相关的图像，一幅图像和下一幅非常接近。在时间和空间上，事物不会瞬间改变，通常是平滑地改变，可以根据前一个值预测出下一个值。我们可以存储一幅基础图像，随后只存储下一幅图像的修正部分。

小波（Wavelets）

　　仍然以8×8的块为例，它的小波基是8个由1,0,-1构成的正交向量：

　　这是8维空间的8个向量，叫做小波。这组基有很多从1到-1的跳跃，实际上这只是小波的一个简单选择，还有很多更精细的选择。这里要做的是基变换，就是将标准基下的向量p表示为小波基的线性组合，并求出线性组合的参数c：

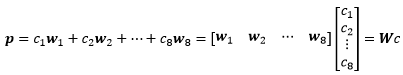
　　这是一个线性变换，W就是描述这个变换的矩阵，它以小波向量为列向量，称为小波矩阵。

　　我们的目的是求出小波变换后的输出向量的坐标，即c = W^-1P，一组性质很好的基能够快速求得c的值，性质很好又是几个意思？一是要能够快速求逆，例如快速傅里叶变换，这里也存在小波变换，小波矩阵中的向量都是正交的，因此它的逆等于它的转置，W^-1 = W^T；二是要有良好的压缩率，只要少量基向量就能接近信号量，比如在扔掉w₅的坐标后，只损失了少量的数值。

基变换

　　A矩阵的列向量是一组新的基向量，x是旧基上的向量，x和新基向量坐标的关系是x = Ac。

　　已知一个线性变换T：R⁸→R⁸，当输入空间使用的一组基是v₁,v₂,…,v₈时，线性变换对应的矩阵是A；对于输出空间的另一组基u₁,u₂,…,u₈来说，线性变换对应的矩阵是B。A和B之间有怎样的联系呢？首先要明确T是一个什么样的变换，是一个旋转还是一个投影，或者其它被指明的变换。A和B描述的是同一个线性变换，只不过使用了不同的基，这两个矩阵是相似矩阵，B = M^-1AM，M是基变换矩阵。

　　

　　关于如何使用傅立叶向量进行图像压缩，可以参考冈萨雷斯的《数字图像处理》，写的非常详细。

---

　　出处：微信公众号 "我是8位的"

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注作者公众号“我是8位的”