线性代数笔记26——傅立叶级数
法国数学家傅里叶发现，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示（选择正弦函数与余弦函数作为基函数是因为它们是正交的），后世称傅里叶级数为一种特殊的三角级数。
构建傅立叶级数的基础
如果有一组n维空间的标准正交基向量q1,q2,…,qn，则n维空间内的任意向量v都可以用这组基的线性组合表示：
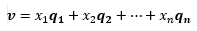
正交基向量：q1,q2,…,qn中的向量两两垂直（更多内容参考 线性代19——格拉姆-施密特正交化）。
对于标准正交向量来说，当i≠j时，qiTqj=0，当i=j时，qiTqj=1，可以根据这一特性在等式两侧同时乘以qiT，从而得到每个分量的系数xi的表达式：
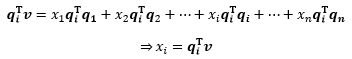
也可以用矩阵相乘的方式表示v：
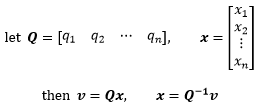
由于Q的列是标准正交的，所以Q的逆等于Q的转置：
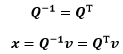
上述内容的关键是Q中的向量是标准正交的，标准正交也是在构建傅里叶级数的基础。
傅立叶级数
对于任意一个周期函数f(x)，都可以使用傅里叶级数展开：
与之前有限个标准正交向量线性组合成的矩阵不同，这个维度是无限的，但关键的性质还是正交，正交性对sinx和cosx仍然成立，这使得傅里叶级数有意义，它的一组基是1, cosx, sinx, cos2x, sin2x…
函数的正交性
我们知道两个向量正交的含义，并且可以用点积等于0判断两个向量的正交性，这种判断方式也可以应用到函数上，但是函数的点积是什么？
v和w是Rn空间内的两个正交向量，这意味着二者的点积为0：
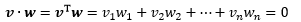
与向量的点积展开式不同，函数是连续的，假设有两个函数f(x)和g(x)，f(x)的周期是2π，我们希望尽可能用fTg的方式表示连续的累加，使得函数点积与向量点积的概念一致。积分正是函数连续累加的概念：
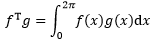
由此可以验证sinx和cosx是正交的：
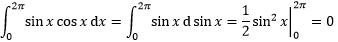
用相同的方式也可以验证cosx和cos2x, sin2x…是正交的。
采用和标准正交向量相同的方式求得傅里叶级数的a1系数：
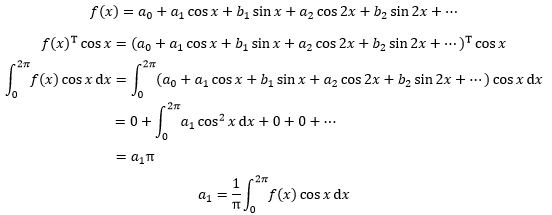
同理可以求得其它系数。
作者：我是8位的
出处：http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！
扫描二维码关注作者公众号“我是8位的”
