数据分析(3)——数据描述
在前面的文章中介绍了平均数和数据的尺度,但仅仅通过它们来描述数据是不够的,还需要通过更多的度量描述数据。
测度中心
上一章已经介绍过测度中心(measure of center),测度中心也被称为数据平衡点,能够在某种程度上对数据进行概括。
测度中心虽然是描述数据的一种简便的方法,但它存在有很多局限性。下表是两个篮球运动员在上个月比赛的得分:
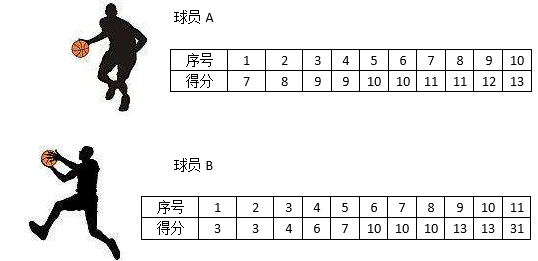
得分表中有意识地将得分从低到高排序。下面的代码计算了A和B的均值和中位数:
1 import numpy as np 2 3 A = [7, 8, 9, 9, 10, 10, 11, 11, 12, 13] 4 B = [3, 3, 4, 6, 7, 10, 10, 10, 13, 13, 31] 5 mu_A, mu_B = np.mean(A), np.mean(B) # 均值 6 median_A, median_B = np.median(A), np.median(B) # 中位数 7 print('mu_A = {}, mu_B = {}'.format(mu_A, mu_B)) # mu_A = 10.0, mu_B = 10.0 8 print('median_A = {}, median_B = {}'.format(median_A, median_B)) # median_A = 10.0, median_B = 10.0
均值A的描述较为恰当,但是B就不一定了。B的离群数据过多,这些数据将极大地影响均值。虽然中位数受离群数据影响较小,但仍不能完整地描述B的特性,此时我们需要寻求数据的其它指标。
数据的距
数据的全距
测度中心用于量化数据的中心,数据的全距则用于量化数据的离散程度。
全距的计算方式很简单,使用数据的最大值减去最小值,仅此而已,它只是对数据离散程度极其基本的描述。
1 A = [7, 8, 9, 9, 10, 10, 11, 11, 12, 13] 2 B = [3, 3, 4, 6, 7, 10, 10, 10, 13, 13, 31] 3 range_A, range_B = max(A) - min(A), max(B) - min(B) # 全距 4 print('range_A = {}, range_B = {}'.format(range_A, range_B)) # range_A = 6, range_B = 28
数据的最小值和最大值分别是全距的下界和上界,二者间的距离就是数据的全距:

全距是由数据的极值计算得出的,仅仅度量了数据的宽度,并且不能指出数据是否包含了异常值,因此全距的使用场景十分有限,很多时候使用全距仅仅是因为它很简单。
全距有一些典型的使用场景:在算法分析时,虽然我们用大O表示法表达算法在平均情况下的效率,但是我们对算法在最好和最差情况的效率依然有很大的兴趣;在软件项目的任务评估时,一个重要的指标是“最坏情况下的完成时间”,毕竟项目进度并不总是那么令人欢欣鼓舞。如此看来,全距并不是那么一无是处。
四分位距
首先要明确的是,四分位和四分卫没有半点关系。

既然全距很容易受异常值影响,那么忽略异常值不就可以了吗?对于B球员来说,可以忽略状态及佳和极差的得分。现在又来了球员C,他的得分情况:
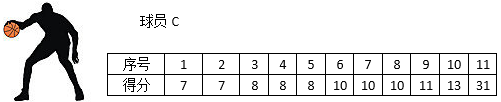
31分远远高出了其他场次,因此忽略31分。现在问题产生了,B球员和C球员采用了不同的异常值忽略方式——B忽略了最低分,而C没有,比较使用不同方式处理的数据,是数据分析的大忌。
忽略异常值的一种较好的方式是使用四分位距。首先将数据排序,然后将数据等分为4份:

从分布上看,四分位距保留了中间靠近均值的50%的数据:
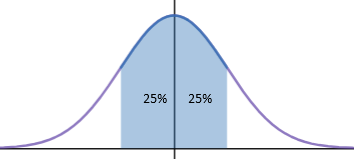
用统一的标准去除了两组数据的异常值。
下四分位数和上四分位数的计算方法和中位数类似。数据集有n个数据,对于下四分位数来说,如果n/4是整数,则下四分位数是n/4位置和n/4 + 1位置的两个数的平均值;如果n/4不是整数,向上取整,该位置的数就是下四分位数。对于上四分位数来说,如果3n/4是整数,则下四分位数是3n/4位置和3n/4 + 1位置的两个数的平均值;如果3n/4不是整数,向上取整,该位置的数就是下四分位数。
球员B共有11个得分,11÷4=2.75,向上取整,下四分位数是数据集中的第3个,下四分位数是4;用11×3÷4=8.25,向上取整,上四分位数是数据集中的第9个,下四分位数是13。该球员的四分距是13 – 4 = 9。

1 A = [7, 8, 9, 9, 10, 10, 11, 11, 12, 13] 2 B = [3, 3, 4, 6, 7, 10, 10, 10, 13, 13, 31] 3 lower_A = np.quantile(A, 1/4, interpolation='lower') # 下四分位数 4 higher_A = np.quantile(A, 3/4, interpolation='higher') # 上四分位数 5 lower_B = np.quantile(B, 1/4, interpolation='lower') 6 higher_B = np.quantile(B, 3/4, interpolation='higher') 7 print('lower_A = {}, higher_A = {}'.format(lower_A, higher_A)) # lower_A = 9, higher_A = 11 8 print('lower_B = {}, higher_B = {}'.format(lower_B, higher_B)) # lower_B = 4, higher_B = 13
当然,你也可以把数据分成任意块,比如分成100块,这对于划分名次很有用。假设某个学生的高考成绩是600分,单从成绩无法知道好坏,但如果说这一年高考的第90个百分数是590分,则可以知道这个考生的分数超过了90%以上的学生。
箱形图
我们经常看到箱形图:
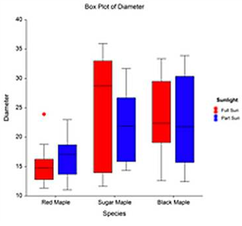
知道了四分位数和四分位距,就不难理解箱形图:

箱形图同时显示了数据的全距、四分距和中位数,通过箱形图可以了解数据的偏斜程度。
1 import matplotlib.pyplot as plt 2 plt.boxplot([A, B], labels = ['player A', 'playerB']) # 箱形图 3 plt.show()
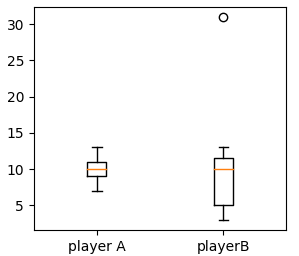
playerB上面还有一个小圆圈,它表示异常值,B球员得31分那场比赛被判定为异常值,箱形图自动将它剔除了。
在正态分布的假设下,μ-3σ<=x<=μ+3σ的区域包含了绝大部分数据,该区域之外的数据被认为是异常的(更多信息可参考:https://mp.weixin.qq.com/s/DgiLzv5sOAS7JeUDk-6fLA):
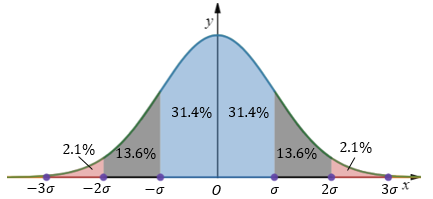
对于箱形图来说,设lower是下四分位数,heigher是上四分位数,range是四分位距,x是某个数据样本,则下面的的不等式判断x是否是异常值:

对于B球员来说:
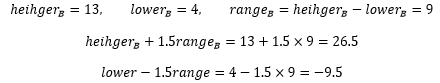
处于-9.5或26.5之外的数值是31,因此31被判定为异常数据。
再谈标准差
方差、均方差和协方差(概率8)中已经讨论过标准差,它衡量了数据的波动程度,即量化数据点偏离均值的程度。通过下面的代码计算两个球员的标准差:
1 A = [7, 8, 9, 9, 10, 10, 11, 11, 12, 13] 2 B = [3, 3, 4, 6, 7, 10, 10, 10, 13, 13, 31] 3 sigma_A, sigma_B = np.std(A), np.std(B) # 标准差 4 print('σ_A = {}, σ_B = {}'.format(sigma_A, sigma_B)) # σ_A = 1.7320508075688772, σ_B = 7.49545316720865
球员A的标准差表示A样本数据的离散程度,可以认为σA近似于A中所有数据点与均值间距离的平均值。样本越分散,远离均值的样本越多,标准差越大。标准差是有单位的,其单位和计算标准差的数据单位一致,A的标准差是球员的得分数。
可以通过柱状图观察数据和标准差的关系:
1 def add_bar(data, mu, sigma, name): 2 ''' 3 添加柱状图 4 :param data: 数据集 5 :param mu: 均值 6 :param sigma: 标准差 7 :param name: 数据集名称 8 ''' 9 length = len(data) 10 plt.bar(left=range(length), height=data, width=0.4, color='green', label=name) 11 plt.plot((0, length), (mu, mu), 'r-', label='均值') # 均值线 12 plt.plot((0, length), (mu + sigma, mu + sigma), 'y-', label='均值+标准差') # 均值线 13 plt.plot((0, length), (mu - sigma, mu - sigma), 'b-', label='均值-标准差') # 均值线 14 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 15 plt.legend(loc='upper left') 16 plt.title('bar of ' + name) 17 18 fig = plt.figure() 19 fig.add_subplot(1, 2, 1) 20 add_bar(A, mu_A, sigma_A, 'A') 21 fig.add_subplot(1, 2, 2) 22 add_bar(B, mu_B, sigma_B, 'B') 23 plt.show()
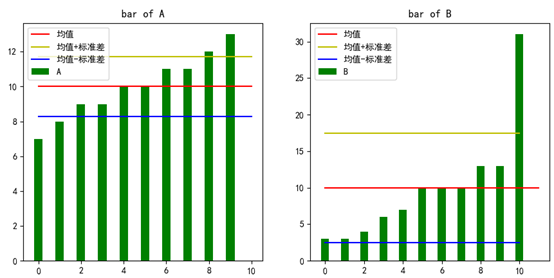
中间红线是均值。黄线和蓝线分别表示均值加减标准差,标准差越大,黄线和蓝线之间的距离也越大,说明数据的离散程度越大。在两条线之外的数据被认为是离群数据。
变异测度
测度中心和标准差都可以描述数据集的特征,二者都是有单位的,如果想要比较两个不同的数据集,特别对不同尺度的数据集进行横向比较,就需要有一种方式去掉单位。
变异系数(coefficient of variation)是标准差和均值的比率,二者相除去掉了单位,并对标准差进行了标准化处理,这种测度也称为变异测度。
假设下表是NBA中锋和控球后卫的身高数据:

可以看到,中锋的平均身高较高,但变异系数只有2.4%,说明作为球队中最高大的队员,各中锋之间的身高差距不大。控球后卫虽然平均身高更接近普通人,但变异系数是8.0%,说明各球队控球后卫的身高差异也较为明显,该位置对身高的要求相对较弱。
z分数(z-scorce)
z分数也称相对分数,用于描述单个数据点和均值之间的距离。数据点和z分数的计算方法是:
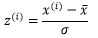
x(i)表示第i个数据点,σ是样本的标准差,带上帽子的x是均值。
标准差近似于所有数据点与均值间距离的平均值,z分数是单个数据点和均值间的距离,更确切地说,是标准化后单个数据点和均值间的距离。
1 z_source_A = (np.array(A) - mu_A) / sigma_A 2 z_source_B = (np.array(B) - mu_B) / sigma_B 3 print('z_source_A =', z_source_A) 4 print('z_source_B =', z_source_B)
z_source_A = [-1.73205081 -1.15470054 -0.57735027 -0.57735027 0. 0. 0.57735027 0.57735027 1.15470054 1.73205081]
z_source_B = [-0.9338995 -0.9338995 -0.80048529 -0.53365686 -0.40024264 0. 0. 0. 0.40024264 0.40024264 2.80169851]
对于的z分数来说,均值的z分数是0,均值加标准差的z分数是1,均值减标准差的z分数是-1:
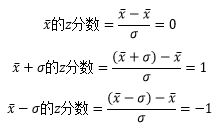
1 def add_z_bar(z_source, name): 2 ''' 添加z_source柱状图 ''' 3 length = len(z_source) 4 plt.bar(left=range(length), height=z_source, width=0.4, color='green', label=name) 5 plt.plot((0, length), (0, 0), 'r-', label='z_source of μ') 6 plt.plot((0, length), (1, 1), 'b-', label='z_source of μ') 7 plt.plot((0, length), (-1, -1), 'y-', label='z_source of μ') 8 9 plt.title('bar of ' + name) 10 fig = plt.figure() 11 # plt.subplots_adjust(wspace=0.5, hspace=0.5) 12 fig.add_subplot(2, 1, 1) 13 add_z_bar(z_source_A, 'z source of A') 14 fig.add_subplot(2, 1, 2) 15 add_z_bar(z_source_B, 'z source of B') 16 plt.show()
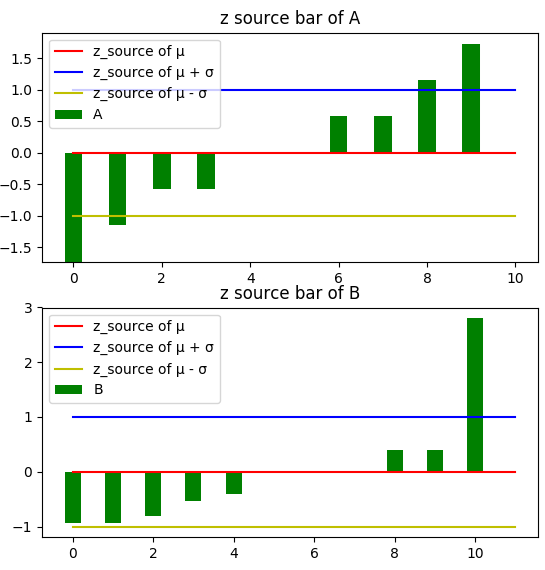
低于均值的数据,z分数是负值;高于均值的数据,z分数是正值;等于z分数的数据,均值为0。下图可以看出z分数和均值的关系:

相关系数
相关系数是描述两个变量间关联性强弱的量化指标。数据的各个特征之间存在关联关系是机器学习模型的重要假设,预测能够成立的原因正是由于特征间存在某种相关性。
相关系数的值介于-1到1之间。两个特征间的关系越强,相关系数越接近±1;关系越若,越接近0。接近+1,表示一个指标增加了,另一个也随之增加;接近-1,表示一个指标增加了,另一个指标将降低。
成年男性的脚长约等与身高的1/7,下面的代码生成了200个身高和脚长的正态分布数据:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import pandas as pd 4 5 def create_data(count=200): 6 ''' 7 构造2维训练集 8 :param model: train:训练集, test:测试集 9 :param count: 样本数量 10 :return: X1:身高维度的列, X2:脚长维度的列表 11 ''' 12 np.random.seed(21) # 设置seed使每次生成的随机数都相等 13 X1 = np.random.normal(1.7, 0.036, count) # 生成200个符合正态分布的身高数据 14 low, high = -0.01, 0.01 15 # 设置身高对应的脚长,正常脚长=身高/7±0.01 16 X2 = X1 / 7 + np.random.uniform(low=low, high=high, size=len(X1)) 17 return X1, X2 18 19 X1, X2 = create_data() 20 df = pd.DataFrame({'height':X1, 'foot':X2}) 21 print(df.head()) # 显示前5个数据
height foot
0 1.698129 0.250340
1 1.695997 0.233121
2 1.737505 0.247780
3 1.654757 0.238051
4 1.726834 0.241137
身高和脚长的维度不同,1厘米对于身高来说相差不大,但对于脚长来说就很大了。为了寻找关联关系,需要对两个维度进行标准化处理,将二者压缩到统一尺度。
1 from sklearn import preprocessing 2 3 # 使用z分数标准化 4 df_scaled = pd.DataFrame(preprocessing.scale(df), columns=['height_scaled', 'foot_scaled']) 5 print(df_scaled.head())
sklearn的preprocessing使用了z分数标准化,结果如下:
height_scaled foot_scaled
0 -0.051839 0.959658
1 -0.110551 -1.389462
2 1.032336 0.610501
3 -1.246054 -0.716968
4 0.738525 -0.295843
现在可以看看两个维度的相关系数:
corr = df_scaled.corr() # 两个维度的相关系数 print(corr)
height_scaled foot_scaled
height_scaled 1.000000 0.614949
foot_scaled 0.614949 1.000000
这个结果告诉我们,身高和脚长关联关系,由于corr()分析的是线性相关,因此即使相关系数为0,也不能明两个特征间没有关系,只能说不存在线性关系。
作者:我是8位的
出处:https://mp.weixin.qq.com/s/ysMdUdcAk9BuXNH9bvqOBg
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号