异常检测(3)——基于概率统计的异常检测(2)
书接上文,继续讨论基于多元正态分布的异常检测算法。
现在有一个包含了m个数据的训练集,其中的每个样本都是一个n维数据:
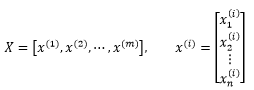
可以通过下面的函数判断一个样本是否是异常的:
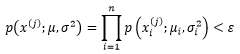
我们的目的是设法根据训练集求得μ和σ,以得到一个确定的多元分正态布模型。具体来说,通过最大似然估计量可以得出下面的结论:
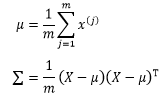
其中Σ是协方差对角矩阵,最终求得的多元正态分布模型可以写成:

关于最大似然估计量、协方差矩阵和多元正态分布最大似然估计的具体推导过程,可参考:
代码:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from mpl_toolkits.mplot3d import Axes3D 4 5 def create_data(model='train', count=200): 6 ''' 7 构造2维训练集 8 :param model: train:训练集, test:测试集 9 :param count: 样本数量 10 :return: X1:第1纬度的列, X2:第2维度的列表 11 ''' 12 np.random.seed(21) # 设置seed使每次生成的随机数都相等 13 X1 = np.random.normal(1.7, 0.036, count) # 生成200个符合正态分布的身高数据 14 low, high = -0.01, 0.01 15 if model == 'test': 16 low, high = -0.05, 0.05 17 # 设置身高对应的鞋码,正常鞋码=身高/7±0.01 18 X2 = X1 / 7 + np.random.uniform(low=low, high=high, size=len(X1)) 19 return X1, X2 20 21 def plot_train(X1, X2): 22 ''' 23 可视化训练集 24 :param X1: 训练集的第1维度 25 :param X2: 训练集的第2维度 26 ''' 27 fig = plt.figure(figsize=(10, 4)) 28 plt.subplots_adjust(hspace=0.5) # 调整子图之间的上下边距 29 # 数据的散点图 30 fig.add_subplot(2, 1, 1) 31 plt.scatter(X1, X2, color='k', s=3., label='训练数据') 32 plt.legend(loc='upper left') 33 plt.xlabel('身高') 34 plt.ylabel('脚长') 35 plt.title('数据分布') 36 # 身高维度的直方图 37 fig.add_subplot(2, 2, 3) 38 plt.hist(X1, bins=40) 39 plt.xlabel('身高') 40 plt.ylabel('频度') 41 plt.title('身高直方图') 42 # 脚长维度的直方图 43 fig.add_subplot(2, 2, 4) 44 plt.hist(X2, bins=40) 45 plt.xlabel('脚长') 46 plt.ylabel('频度') 47 plt.title('脚长直方图') 48 49 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 50 plt.rcParams['axes.unicode_minus'] = False # 解决中文下的坐标轴负号显示问题 51 plt.show() 52 53 def fit(X_train): 54 ''' 55 拟合数据,训练模型 56 :param X_train: 训练集 57 :return: mu:均值, sigma:方差 58 ''' 59 global mu, sigma 60 X = np.mat(X_train.T) 61 m, n = X.shape 62 mu = np.mean(X, axis=1) # 计算均值μ,axis=1表示对每一个子数组计算均值 63 sigma = np.mat(np.cov(X)) # 计算Σ,等同于(X - mu) * (X - mu).T / len(X_train) 64 65 def gaussian(X_test): 66 ''' 67 计算正态分布 68 :param X_test: 测试集 69 :return: 数据集的密度值 70 ''' 71 global mu, sigma 72 m, n = np.shape(X_test) 73 sig_det = np.linalg.det(sigma) # 计算det(Σ) 74 sig_inv = np.linalg.inv(sigma) # Σ的逆矩阵 75 r = [] 76 for x in X_test: 77 x = np.mat(x).T - mu 78 g = np.exp(-x.T * sig_inv * x / 2) * ((2 * np.pi) ** (-n / 2) * (sig_det ** (-0.5))) 79 r.append(g[0, 0]) 80 return r 81 82 def sel_epsilon(X_train): 83 ''' 84 选择合适的ε 85 :param X_train: 86 :return: ε 87 ''' 88 g_val = gaussian(X_train) 89 return np.min(g_val) + 0.0001 90 91 def predict(X): 92 ''' 93 检测训练集中的数据是否是正常数据 94 :param X: 待预测的数据 95 :return: P1:数据的密度值, P2:数据的异常检测结果,True正常,False异常 96 ''' 97 P1 = gaussian(X) # 数据的密度值 98 P2 = [p > epsilon for p in P1] # 数据的异常检测结果,True正常,False异常 99 return P1, P2 100 101 def plot_predict(X): 102 '''可视化异常检测结果 ''' 103 P1, P2 = predict(X) 104 normals_idx = [i for i, t in enumerate(P2) if t == True] # 正常数据的索引 105 outliers_idx = [i for i, t in enumerate(P2) if t == False] # 异常数据的索引 106 normals_x = np.array([X[i] for i in normals_idx]) # 正常数据 107 outliers_x = np.array([X[i] for i in outliers_idx]) # 异常数据 108 109 fig1 = plt.figure(num='fig1') # 散点图 110 ax = Axes3D(fig1) 111 ax.scatter(normals_x[:,0], normals_x[:,1], 112 [P1[i] for i in normals_idx], label='正常数据') 113 ax.scatter(outliers_x[:,0], outliers_x[:,1], 114 [P1[i] for i in outliers_idx], c='r', marker='^', label='异常数据') 115 ax.set_title('共有{}个异常数据'.format(len(outliers_idx))) 116 ax.axis('tight') # 让坐标轴的比例尺适应数据量 117 ax.set_xlabel('身高') 118 ax.set_ylabel('脚长') 119 ax.set_zlabel('p(x)') 120 ax.legend(loc='upper left') 121 122 n = 100 123 xs, ys = np.meshgrid(np.linspace(min(X1_train), max(X1_train), n), 124 np.linspace(min(X2_train), max(X2_train), n)) 125 zs = [gaussian(np.c_[xs[i], ys[i]]) for i in range(n)] 126 127 fig2 = plt.figure(num='fig2') 128 ax = Axes3D(fig2) 129 # 3维空间的拟合曲面 130 ax.plot_surface(xs, ys, zs, alpha=0.5, cmap=plt.get_cmap('rainbow')) 131 ax.scatter(normals_x[:, 0], normals_x[:, 1], 132 [P1[i] for i in normals_idx], label='正常数据') 133 ax.scatter(outliers_x[:, 0], outliers_x[:, 1], 134 [P1[i] for i in outliers_idx], c='r', marker='^', label='异常数据') 135 ax.axis('tight') # 让坐标轴的比例尺适应数据量 136 ax.set_xlabel('身高') 137 ax.set_ylabel('脚长') 138 ax.set_zlabel('p(x)') 139 ax.legend(loc='upper left') 140 141 fig3 = plt.figure(num='fig3') 142 plt.scatter(normals_x[:, 0], normals_x[:, 1], s=30., c='k', label='正常数据') 143 plt.scatter(outliers_x[:, 0], outliers_x[:, 1], c='r', marker='^', s=30., label='异常数据') 144 plt.contour(xs, ys, zs, 80, alpha=0.5) # 等高线 145 plt.axis('tight') # 让坐标轴的比例尺适应数据量 146 plt.xlabel('身高') 147 plt.ylabel('脚长') 148 plt.legend(loc='upper left') 149 150 plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 151 plt.rcParams['axes.unicode_minus'] = False # 解决中文下的坐标轴负号显示问题 152 plt.show() 153 154 if __name__ == '__main__': 155 X1_train, X2_train = create_data() 156 plot_train(X1_train, X2_train) 157 158 X_train = np.c_[X1_train, X2_train] 159 mu, sigma = np.mat([]), np.mat([]) 160 fit(X_train) 161 epsilon = sel_epsilon(X_train) 162 163 X_test = np.c_[create_data(model='test', count=20)] 164 X = np.r_[X_train, X_test] 165 plot_predict(X)
为了简单起见,我们认为X_train 中的数据全部是正常数据。fit(X_train)计算多元正态分布的模型参数,gaussian(X_test)根据目标函数计算样本的多元正态分布密度值。在知道了算法原理的请看下,fit(X_train)和gaussian(X_test)都毫无神秘性可言。
predict(X)将对X中的所有样本进行检测,并返回X对应的检测结果列表,列表中的元素是一个二元组,第一个元素记录x(i)是否是正常数据,第二个元素记录p(x(i);μ,Σ)。由于已经假设了X_train中全部是正常数据,因此这里选择X_train中最小的密度值作为ε。
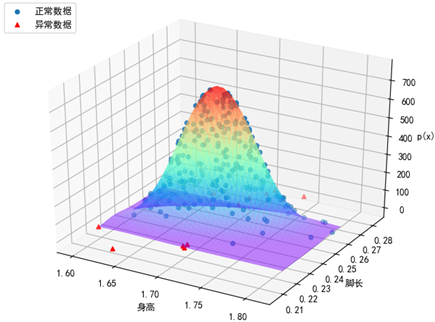
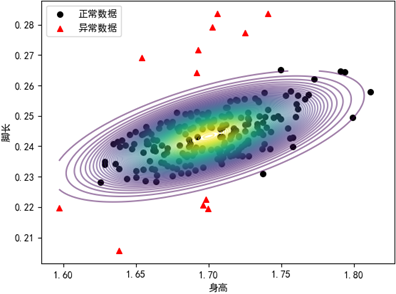
X_test中的20个测试数据是可能的异常样本。plot_predict(X)展示了空间样本点、空间拟合曲面和等高线:

作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公作者众号“我是8位的”




 浙公网安备 33010602011771号
浙公网安备 33010602011771号