最小二乘法（2）——多项式函数能够拟合非线性问题原理

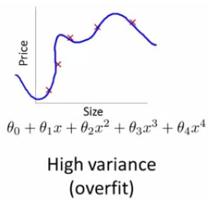
　　一个复杂的多项式可以“过拟合”任意数据，言外之意是多项式函数可以接近于任何函数，这是什么道理呢？

泰勒公式

　　欲理解多项式函数的过拟合，必先理解泰勒公式。

　　泰勒公式是一种计算近似值的方法，它是一个用函数某点的信息描述在该点附近取值的公式。已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来逼近函数在这一点的邻域中的值。

　　如果f(x)在x₀处具有任意阶导数，那么泰勒公式是这样的：

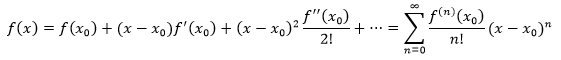
　　上式中的幂级数称为f(x)在x₀点的泰勒级数。（0的阶乘是1）

  　 更多泰勒公式的介绍可参考  单变量微积分笔记31——幂级数和泰勒级数

 

泰勒公式的应用

　　来看一个泰勒公式的应用。假设一个小偷盗取了一辆汽车，他在高速公路上沿着一个方向行驶，车辆的位移s是关于时间t的函数。警方接到报案后马上调取监控，得知在零点（t=0时刻）小偷距车辆丢失地点的位移是s₀。现在的时间是0:30，警方想要在前方设卡，从而能在凌晨1点拦住小偷，应该在哪里设卡呢？

　　我们知道车辆在0点时的位移是s₀，现在想要知道凌晨1点时车辆的位置：

　　可以直接使用泰勒公式：

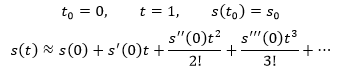
　　泰勒公式可以无限展开，展开得越多，越逼近真实值，并且越到后面的项，对结果的影响越小，我们认为0和1非常接近，所以只展开到2阶导数：

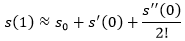
　　这就是最终结果，在此处设卡最有可能在第一时间拦住小偷。

在0点处的泰勒展开

　　在使用泰勒公式时，经常取x₀=0。

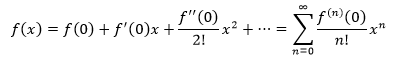
　　f(x)=e^x是一个可以用泰勒公式展开的例子，下面是e^x在x₀=0处的泰勒展开：

　　当x=1时，还附带得到了e的解释：

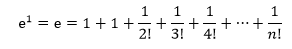
　　我们使用一个很难处理的积分解释泰勒展开的意义，对正态分布进行积分：

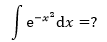
　　常规的方法很难处理。现在，由于被积函数与e^x相似，我们又已经知道e^x的展开式，所以可以进行下面的变换：

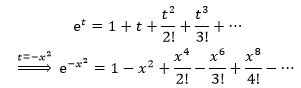
　　将exp(-x²)左右两侧同时积分：

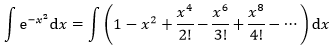
　　很容易计算右侧的每一项积分。

　　这个例子展示了幂级数展开的意义——把质的困难转化成量的复杂。展开前求解函数的值很困难，展开后是幂级数，虽然有很多很多项，但是每一项都是幂函数，都很容易求解，于是，只要对展开后的函数求和，就能得到展开前的函数的值。

为什么在0点处展开

　　当x₀=0时，可以极大地简化泰勒展开式。之前说泰勒公式是一个用函数某点的信息描述在该点附近取值的公式，一个函数中的某点如果距离0很远怎么办呢？实际上泰勒公式也能够逼近函数在距离0很远处的取值，只不过此时只展开到2阶导数是不够的，需要展开很多项，展开的越多，越能逼近该点。以标准正态分布函数f(x)=exp(-x²)为例，虽然它在二阶展开使与原函数相差较大，但是当展开到40阶时就已经非常接近原函数了。

多项式函数

　　理解了泰勒公式后，再回到问题的原点，看看多项式函数为什么可以接近于任何函数。

　　仍然以标准正态分布为例，它在x₀ = 0点处的10阶泰勒展开是：

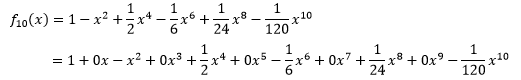
　　如果将每一项中的xⁱ都看作一个维度，那么这个多项式函数可以写成多元线性回归的形式：

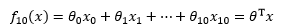
　　这就将一个一元的非线性问题转换成了多元的线性问题，从而利用最小二乘法求得模型参数。

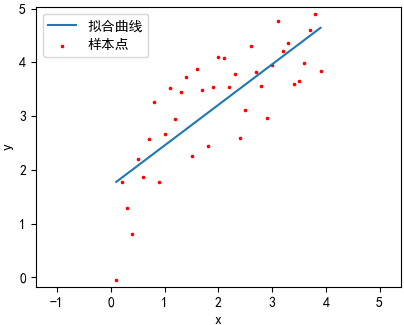
　　下面的代码以ln(2x) + 2为原函数，生成40个在-1~1之间随机震荡的数据点，并使用线性回归和多项式回归拟合数据点：

 

import numpy as np
import matplotlib.pyplot as plt

def create_datas():
    '''
    生成10个待拟合的点
    :return: xs, ys
    '''
    xs = np.arange(0.1, 4, 0.1)
    # y = ln(2x) + noize,  -1 <= noize <= 1
    ys = np.array([np.log(x * 2) + 2 + np.random.uniform(-1, 1) for x in xs])

    return xs, ys

class Regression():
    ''' 回归类 '''
    def __init__(self, xs, ys):
        '''
        :param xs: 输入数据的特征集合
        :param ys: 输入数据的标签集合
        '''
        self.xs, self.ys = xs, ys
        self.theta = None # 模型参数

    def train_datas(self, xs=None):
        '''
        重新构造训练样本的特征和标签
        :param xs: 输入数据的特征集合
        :return: 矩阵形式的训练样本特征和标签
        '''
        xs = self.xs if xs is None else xs
        X = self.train_datas_x(xs)
        Y = np.c_[ys] # 将ys转换为m行1列的矩阵
        return X, Y

    def train_datas_x(self, xs):
        '''
        重新构造训练样本的特征
        :param xs: 输入数据的特征集合
        :return: 矩阵形式的训练样本特征
        '''
        m = len(xs)
        # 在第一列添加x0,x0=1,并将二维列表转换为矩阵
        X = np.mat(np.c_[np.ones(m), xs])
        return X

    def fit(self):
        ''' 数据拟合 '''
        X, Y = self.train_datas()
        self.theta = (X.T * X).I * X.T * Y

    def predict(self, xs):
        '''
        根据模型预测结果
        :param xs: 输入数据的特征集合
        :return: 预测结果
        '''
        X = self.train_datas(xs=xs)[0]
        return self.theta.T * X.T

    def show(self):
        ''' 绘制拟合结果 '''
        plt.figure()
        plt.scatter(self.xs, self.ys, color='r', marker='.', s=10)  # 绘制数据点
        self.show_curve(plt) # 绘制函数曲线
        plt.xlabel('x')
        plt.ylabel('y')
        plt.axis('equal')
        plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
        plt.rcParams['axes.unicode_minus'] = False  # 解决中文下的坐标轴负号显示问题
        plt.legend(['拟合曲线', '样本点'])
        plt.show()

    def show_curve(self, plt):
        ''' 绘制函数曲线 '''
        pass

    def global_fun(self):
        ''' 返回目标函数 '''
        gf = ['(' + str(t[0, 0]) + str(i) + ')x^' + str(i) for i, t in enumerate(self.theta)]
        return ' + '.join(gf)

class Linear(Regression):
    ''' 线性模型'''
    def show_curve(self, plt):
        '''
        绘制拟合结果
        :param plt: 输入数据的特征集合
        '''
        xx = [self.xs[0], self.xs[-1]]
        yy = self.predict(xx)
        plt.plot(xx, np.array(yy)[0])

class Multinomial(Regression):
    ''' 多项式回归模型 '''
    def __init__(self, xs, ys, n=3):
        '''
        :param xs: 输入数据的特征集合
        :param ys: 输入数据的标签集合
        :param n: 多项式的项数
        '''
        super().__init__(xs, ys)
        self.n = n

    def train_datas_x(self, xs):
        '''
        重新构造训练样本的特征
        :param xs: 输入数据的特征集合
        :return: 矩阵形式的训练样本特征
        '''
        X = super().train_datas_x(xs)
        for i in range(2, self.n + 1):
            X = np.column_stack((X, np.c_[xs ** i])) # 构造样本的其他特征
        return X

    def show_curve(self, plt):
        ''' 绘制函数曲线 '''
        xx = np.linspace(self.xs[0], self.xs[-1], len(self.xs) * 20)
        yy = self.predict(xx)
        plt.plot(xx, np.array(yy)[0], '-')

if __name__ == '__main__':
    xs, ys = create_datas()
    regressions = [Linear(xs, ys), Multinomial(xs, ys), Multinomial(xs, ys, n=5), Multinomial(xs, ys, n=10)]
    for r in regressions:
        r.fit()
        r.show()
        print(r.global_fun())

(1.702537204930)x^0 + (0.75431357262260011)x^1

 

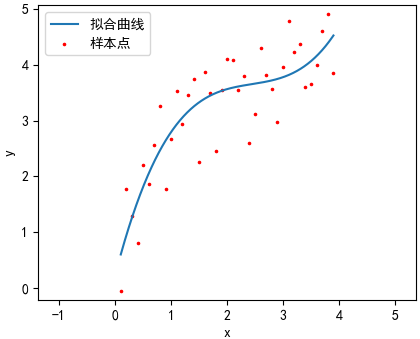
 (0.23422131704216660)x^0 + (3.8713793437217621)x^1 + (-1.51749485964066682)x^2 + (0.206815637166500283)x^3

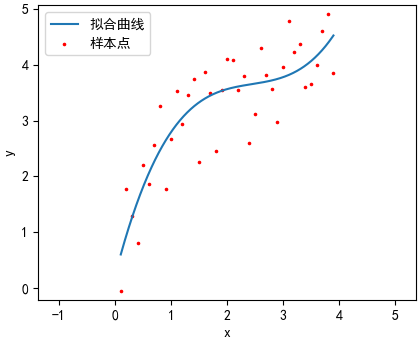
 (0.0023811193415048670)x^0 + (4.707160334405161)x^1 + (-2.03334533257402762)x^2 + (0.095635349482284143)x^3 + (0.130611330518000564)x^4 + (-0.021122013844903465)x^5

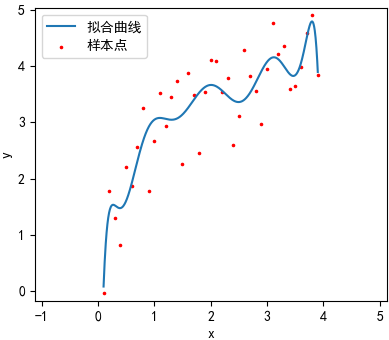
(-4.7285135624557920)x^0 + (77.637488456533421)x^1 + (-377.238590224254552)x^2 + (932.32693158635363)x^3

+ (-1305.30725871564164)x^4 + (1112.9257341435945)x^5 + (-598.57958115210336)x^6

+ (203.91275172701427)x^7 + (-42.641981259587898)x^8 + (4.9915417588645349)x^9 + (-0.250300601937088710)x^10

 　　看来第二、三条曲线的拟合效果比较好，第一幅图欠拟合，四过拟合。

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公作者众号“我是8位的”