概率笔记9——大数定律

　　在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。

　　当我们掷一枚硬币时，说正面朝上的概率是1/2，是这样吗？当你掷十次硬币时，正面朝上的概率可未必是1/2，这个结果带有很强的随机性，并没有什么规律可言。但是当投掷的次数足够多时，规律就呈现出来了。概率研究的是随机现象背后的客观规律，当试验次数趋*于无穷时，正面朝上的频率收敛于1/2概率。

　　大数定律是概率论中讨论随机变量序列的算术*均值向随机变量各数学期望的算术*均值收敛的定律。我觉得还是不要计较概念，关注实际例子就好。

　　以斗地主为例，玩家的水*有高有低，但每个人都有一个真实水*，衡量真实水*的数字特征就是获胜的数学期望。然而高手也不见得每次都会获胜，因为除了实力外，运气也占有很大比重，顶尖高手面对一手烂牌也会束手无策。我们并不能以一局的输赢判断某个人打牌的水*高低，此时运气带来的影响会放大，也就是随机性太大，但是随着打牌的次数增多，高手的成绩会渐渐趋于稳定，他赢的次数会渐渐符合他的真实水*，此时随机性背后的客观规律会逐渐显现出来。

　　我们用一段程序模拟大数定律。这段程序在1~10中随便抽取n个数，然后计算*均值：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

results = []
for n in range(1, 10000):
    nums = np.random.randint(low=1, high=10, size=n)
    results.append(nums.mean())

df = pd.DataFrame({'均值': results})
df.plot()
plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.xlabel('样本数量')
plt.ylabel('样本均值')
plt.show()

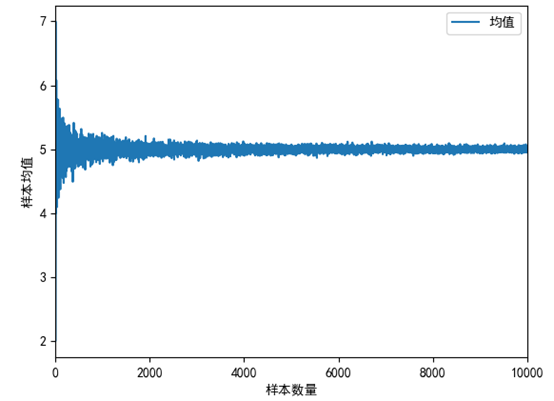
　　可以看到，随着样本的增多，均值逐渐趋*于*稳，随机性对均值的影响也越来越小。

 

　　以下内容是从 保险不是碰运气(大数法则) （https://www.jianshu.com/p/f384357a554d）上抄来的：

　　根据以往的经验，某类汽车每年的损失概率约为2‰，相应的，在收保费时也会按这个损失比例收取。这时，我们可以把一投保的该类汽车看作一次抛硬币或一次掷骰子，如果投保的汽车数量很少，则相当于抛硬币和掷骰子实验中抛掷的次数很少，那么投保的汽车实际发生事故几率与预先估计的2‰，这个比例可能相差较远，对于保险公司而言则容易发生赔付危机；相反，如果有许许多多的车辆投保该保险，就相当于上面实验中抛掷次数相当多，那么实际的事故发生状况当然就会更接*保险公司估计的2‰，这一损失比例，保险公司就不会担心发生赔付危机了。

　　大数定律的实质就在于，通过集合众多性质相同或相*的风险，把单个风险的不确定性变成集体风险的可测性，从而达到分散风险的目的。其实，一家保险公司承保的业务再少，也可以通过再保险制度将全世界的同类业务联系起来，也符合大数定律的要求。

　　有了大数定律这一科学原理，保险公司在保证大量标的存在的前提下，可以预先估计来年将会发生多少事故，并提前做好准备。所以，不用担心，保险公司是真的很“保险”，并不是在碰运气。

 

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonke

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公作者众号“我是8位的”