概率笔记6——多维随机变量
和其它问题一样,概率也可能同时受到多个条件的影响,例如考察某地区中学生的身体素质,随机地选取一名学生,观察学生的身高 X,体重 Y 和肺活量 Z 等指标。随机变量 X,Y,Z 来自同一样本空间,它们的取值可能相互影响。像这样同时考虑的多个随机变量,称为多维随机变量。本章以二维随机变量为例,介绍多维随机变量的相关概念。
联合分布
和一维变量的概率分布类似,联合分布把舞台扩展到了多维,这里的“联合”就是多个随机变量的意思。
假设一个事件受到两个变量x和y的影响,它的联合分布定义为:
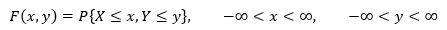
其中X表示具体的取值,x表示变量。
上一章提到过,分布是指概率的累加,是把事件映射为数字,一个二维联合分布的变量取值范围是整个二维平面,但F(x,y)的取值范围是0~1。
离散型
联合概率
联合概率指的是包含多个条件且所有条件同时成立的概率,也叫联合分布率。
用xi和yj的两个随机变量所有可能的取值,P(X=xi, Y=yj)表示在X=xi和Y=yj下事件发生的概率。设P(X=xi, Y=yj)=pij,则下表是二维离散型随机变量(X, Y)的联合概率:
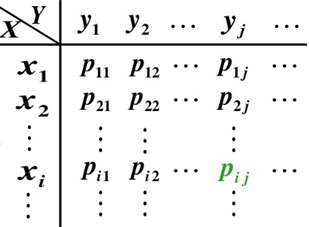
联合分布率实际上是一个矩阵。既然是概率,联合概率也满足下面两个条件:

联合分布
一维随机变量的分布函数:
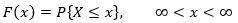
二维随机变量的分布函数:
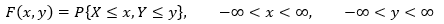
其中:
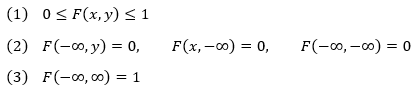
分布函数和分布略有区别,“分布”是指累加概率,“分布函数”是将累加概率函数化。F(x,y)=P{X≤x,Y≤y}是分布函数,它的值是所有在X≤x,Y≤y下的概率分布。
边缘分布
先看表1的第一行,它固定了x=x1,此时在表格右侧加入一列:

p1·表示x的取值固定,y取任意值时的概率分布,即:
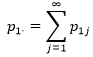
由于p1·是写在表格的边缘,所以称为x=x1的边缘分布。对于任意行来说:
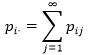
这实际上是在表示X= xi时事件发生的概率。类似的,y=yj的边缘分布是:

条件概率
条件概率是指在A事件发生的条件下,事件B发生的概率,表示为P(B|A),它有一个重要公式:
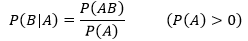
多维随机变量的条件概率公式与此类似,在Y=yj 条件下X=xi的概率:
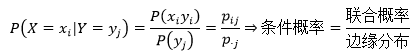
独立性
对于二维离散型随机变量(X, Y)来说,如果满足:
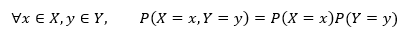
那么这两个随机变量之间是没有相互影响的,称X和Y之间互相独立。反过来也一样,如果满足了独立性,那么必然有上式的关系。
连续型
由于是连续型变量,所以无法像离散型变量那样简单地计算在某一点的概率(概率可以表示为几何度量,点的度量是0,因此算某一点的概率也是0,或者说计算点的概率没有意义),只能计算某一取值范围内的概率,也就是概率分布(概率的累加)。
联合概率密度函数和联合分布
某个地区的人口密度越大,这个地区的人口越多。同样的,概率密度越大,说明这个区域的发生某件事的概率越大。
设F(x,y)是二维连续型随机变量(X,Y)的联合分布函数,如果存在一个非负函数f(x,y),对于任意实数x,y,有:
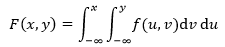
则称f(x,y)是二维连续型随机变量(X,Y)的联合概率密度函数。
u和v在计算后定积分后会被x和y代替。可以对比上一章中一维随机变量的分布函数来理解F(x,y)。概率分布是概率的累加,而累加正好是积分的定义。在几何上,F(x,y)表示了曲面柱体的体积:

假设在R区域上,x1<x<x2, y1<y<y2,那么该区域上的概率分布是:

dydx是R上的面积积元,它是面积无限接近0的小矩形,但不是0。至此,概率和多重积分联系到一起。上式中没有u和v,这是由于已经确定了x和y的取值范围,且f本来就是关于x和y的函数,因此没必要再引入u和v。如果非要使用u和v,那么上式等价于:
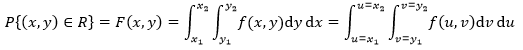
由于F是分布函数,因此在整个定义域上满足:
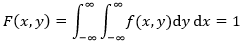
边缘分布和边缘密度函数
联合分布表达的是二维随机变量(X, Y)的整体分布,同时X和Y也有各自的边缘分布。与离散型类似,连续型随机变量的边缘分布是只认为有一个变量,其它变量都看作常量。
X的边缘分布,表示将x看作常量,不管Y的取值:
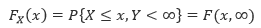
Y的边缘分布,表示将y看作常量,不管x的取值:
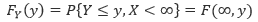
设(X, Y)的联合密度函数是f(x,y),那么(X, Y)的联合分布可以表示为:
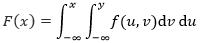
X的边缘分布限定了X的取值是X≤x,y可以取任意值,此时X的边缘分布可以写成:
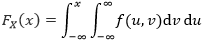
分布代表了累加,连续型分布是用积分表示的,FX(x)表示P{X≤x, Y<∞}的累加,是对dx的积分,因此X的边缘分布的密度函数是上式的内积分:
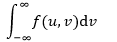
把u,v换成x,y,X的边缘分布的密度函数是:
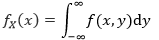
类似的,Y的边缘分布的密度函数是:

条件分布和条件密度函数
条件概率公式:
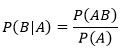
对于连续型变量来说,单点的概率没有意义,因此将上式推广到连续型随机变量后就变成了“分布”,比如给定Y值的条件下X的概率分布。
设(X, Y)的联合密度函数是f(x,y),边缘密度函数是fX(x)和fY(y),如果固定x,则称下式为X=x条件下Y的概率密度:
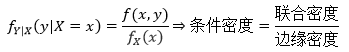
同样,Y=y条件下X的概率密度:
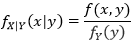
有了概率密度,自然可以求得相应的分布,给定Y值的条件下X的概率分布:
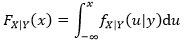
独立性
对于二维连续型随机变量(X, Y)来说,如果满足:

那么这两个随机变量之间是没有相互影响的,称X和Y之间互相独立。反过来也一样,如果满足了独立性,那么必然有上式的关系。
二维均匀分布
设R是平面上的有界区域,面积为A,若二维随机变量(X,Y)具有概率密度:
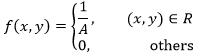
则称(X, Y)在R上服从均匀分布。
如果在R区域上x在x1<x<x2上服从均匀分布,那么X在x1<x<x2的边缘分布的密度函数是:
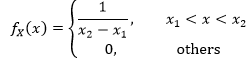
若(X, Y) 服从R区域上的均匀分布,则对于R上的任一子区域D,都有:
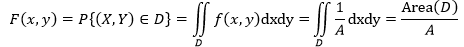
上式实际上是在说,如果(X,Y)在某个区域内服从均匀分布,则意味着(X,Y)在该区域内具有“等可能”性。
二维正态分布
若二维随机变量(X,Y)具有概率密度:
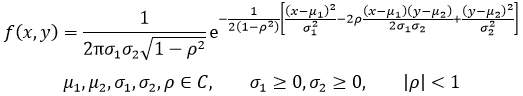
则称(X,Y)服从参数为 的二维正态分布,记作:
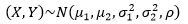
f(x,y)的是一个倒钟型曲面:
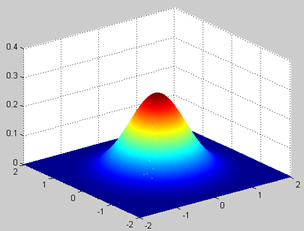
示例
示例1
X服从(0,1)上的均匀分布,在X=x(0<x<1)的条件下,Y在(0,x)内服从均匀分布,f(x,y)=?, 2. fY(y)=?
先看1,X服从某一个区域的边缘分布意味着:
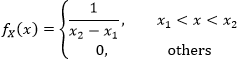
X服从(0,1)上的均匀分布,则x1 = 0, x2 = 1:
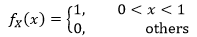
“Y在(0,x)内服从均匀分布”:
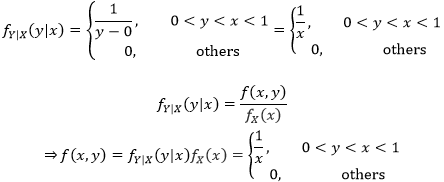
2. Y的边缘分布的密度函数是:
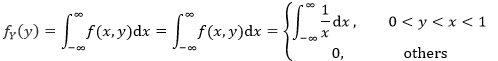
现在只需要确定的积分域即可,由0<y<x<1可知,积分上限是1,下限是y:
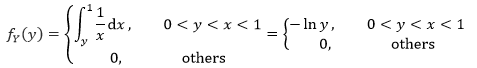
示例2
设二维随机变量(X, Y)的联合概率密度是:
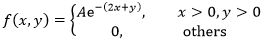
1. A=? 2.求分布函数F(x,y) 3.求概率P{Y≤X}
1. 整个定义域上分布函数满足:
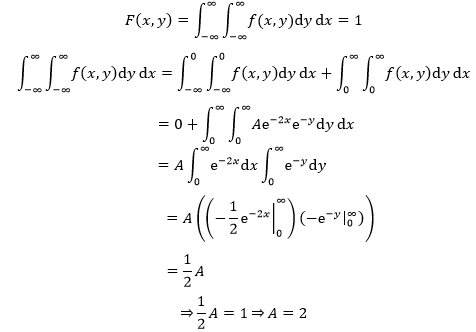
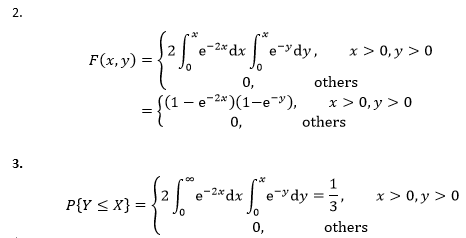
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号