退而求其次(2)——遗传算法
小偷又来了
在搜索的策略(2)——贪心策略中,小偷撬开了一个保险箱,利用贪心法偷走了里面的物品并卖了个好价钱。现在小偷又来了,他光顾了同一个保险箱,保险箱中的物品还和之前一样,有5个物品A,B,C,D,E,它们的体积分别是3,4,7,8,9,价值分别是4,5,10,11,13,只不过每种物品仅有一个。
这次小偷带了一个容量是20的背包,他升级了一下自己的技术,打算使用遗传算法重新编写代码。
遗传算法
达尔文在1859年出版的《物种起源》中系统地阐述了进化论,他认为生物是可变的,是不断进化的,物竞天择,适者生存。进化论很快取代了神创论,成为生物学研究的基石。
遗传算法正是受进化论启发的一种优化算法。二十世纪六十年代初,密切根大学教授Holland开始研究自然和人工系统的自适应行为,通过模拟生物进化过程设计了最初的遗传算法,也称为经典遗传算法(Genetic Algorithms,GA)。
原理和步骤
遗传算法和生物进化过程及其相似。算法首先从问题的解空间中随机选择一部分解作为初始种群,将种群中的每一个解视为一个生物个体。之后让种群中的全部个体朝既定的目标(最优解)前进,并且在前进过程中展开生存竞争。此时自然法则将产生作用,在竞争中胜出者会被保留下来,失败者则被淘汰,为胜出者腾出空间。接下来,胜出者会通过交叉和变异的方式产生出许多新的个体代替失败者,以保持种群总量不变。最后,新种群构成了“下一代”,它们将继续朝目标前进,并再次展开竞争……不断重复下去,由于每一代都是胜出者的子孙,所以我们有理由相信,新一代在整体上强于上一代,整个种群将朝着更高级的进化体逐步前进:

基因编码
生物遗传靠的是基因,解读基因编码对于绝大多数人来说是个神秘的工作。受生物学启发的遗传算法也有基因编码的概念,而且基因编码是遗传算法的首要问题,没有基因编码,就没有遗传。
基因、染色体、嘧啶、嘌呤……这些概念有些唬人了,实际上遗传算法中的基因编码远没有生物科学中的那么神秘,它可以简单地理解成,以计算机存储数据的形式表达问题的解。
一种常用且自然的编码方式是二进制编码。对于保险柜中的每种物品来说,要么拿走,用1表示;要么不拿,用0表示,因此可以用一个5位的二进制数表示一种盗窃方案:

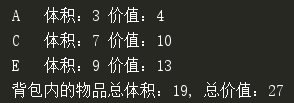
字符串”10101”表示小偷偷走了A、C、E三个物品,可以用print_solution方法来解码:
1 GOODS_LIST = [('A', 3, 4), ('B', 4, 5), ('C', 7, 10), ('D', 8, 11), ('E', 9, 13)] 2 3 def print_solution(code): 4 ''' 5 打印解决方案 6 :param code: 二进制基因编码 7 ''' 8 size_sum, value_sum, = 0, 0 9 for i, x in enumerate(code): 10 if x == '1': 11 gtype, size, value = GOODS_LIST[i] 12 print('\t{0}\t体积:{1}\t价值:{2}'.format(gtype, size, value)) 13 size_sum += size 14 value_sum += value 15 print('\t背包内的物品总体积:{0},\t总价值:{1}'.format(size_sum, value_sum))
保险柜中的物品清单用一个简单的三元组表示,('A', 3, 4)表示物品A的体积是3,价值是4。”10101”的解码结果:
编码方式还有很多,比如浮点数编码、整数编码、顺序编码、格雷编码、字符编码、矩阵编码等,不同的编码方式可能会对配对和变异的设计产生影响,但是无论使用哪种编码,都需要保证编码值能够表示解空间中的所有解,并且能够和这些解一一对应。我们会在后续看到不同于二进制编码的其它编码方式。
种群和个体
生物进化是以群体的方式进行的,这个群体被称为种群。种群中的每种生物都是一个个体,有着自己的基因编码。
盗窃方案的基因编码共有25=32种,每一中编码都是一个个体,种群的大小应当小于解空间中候选解的数量。我们令种群的大小是5,并使用随机挑选的方式产生初始种群:
1 POPULATION_SIZE = 5 # 种群数量 2 3 def init_population(): 4 ''' 构造初始种群 ''' 5 population = [] 6 code_len = len(GOODS_LIST) # 编码长度 7 for i in range(POPULATION_SIZE): 8 population.append(''.join(random.choices(['0', '1'], k=code_len))) 9 return population
一般来说,种群的大小一旦确定就无需改变。
对于小偷来说,并不是所有的编码方式都是有效的解,比如11101,解码的结果是小偷偷走了A、B、C、E四个物品,其体积总量是23,超过了背包的容量。一种应对策略是在初始化种群是加入判断,排除无效的解,这在后续的配对和变异是也需要类似的判断;另一种是让无效编码永远不会被选中,这需要在适应度的取值上做点文章。
适应度评估
种群中的每个个体都可以通过适应度函数计算出适应度的值。适应度高的将会有较大概率生存下来,并将基因遗传给下一代;适应度低的,则有较大的概率被淘汰。适应度函数的另一个较为通俗名称是成本函数,至于应该淘汰成本低的还是成本高的,完全取决于你自己。
偷窃方案的适应度评估很容易,只要计算价背包中物品的总价值就可以了,如果物品撑爆了背包,让总价值返回0:
1 V_BAG = 20 # 背包的容量 2 3 def fitness_fun(code): 4 ''' 5 适应度评估 6 :param code: 二进制基因编码 7 :return: 适应度评估值 8 ''' 9 size_sum, sum_value = 0, 0 # 物品的总体积,物品的总价值 10 for i, x in enumerate(code): 11 if x == '1': 12 _, size, value = GOODS_LIST[i] 13 size_sum += size 14 sum_value += value 15 if size_sum > V_BAG: # 背包被撑爆时,适应度为0 16 sum_value = 0 17 break 18 return sum_value
种群选择
有了适应度评估值,就可以开始残酷的生存竞争。从种群中选择某些个体形成下一代的父群体,以便将较为优秀的基因遗传到下一代。选择策略有很多,常用的有轮盘赌法、精英保留法、锦标赛法等,不同的策略对遗传算法的交叉设计、变异设计和整体性能都将产生影响。
1. 轮盘赌法
轮盘赌是一种依靠运气的赌博方式。在赌博时,轮盘逆时针转动,掌盘人把一个小球在微凸的轮盘上以顺时针方向滚动。小球速度逐渐下降,最后落入某个对应着号码和颜色的金属格中。

轮盘赌算法和赌场中的轮盘赌类似,基本思想是把每个个体的适应度按比例转换为被选中的概率。假设种群中有 个个体, ,第 个个体的适应度是 ,群体的总适应度是所有个体适应度之和,用 表示。一个显而易见的策略是用 表示第 个个体被选中的概率。如果盗窃方案的初始种群是['10010', '00010', '10100', '01100', '11010'],那么每个个体被选中的概率:
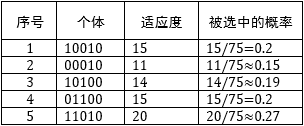
根据上表制作一个轮盘,每个概率都相当于轮盘中的一个方格,概率值越大,方格也越大:
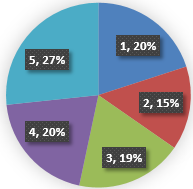
种群中的适应度较高的精英(适应度较高的个体)理应获得较大的选中概率,但某个种群的最优解并不一定在全局最优解附近:
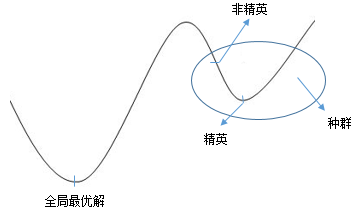
轮盘赌策略可以让所有个体均有几率被选中,在重视精英的同时,也给非精英们留下一点生存的机会。如何在计算机上实现这种策略呢?
我们首先按照个体的序号,顺序地计算每个个体的概率分布,用qi 表示:
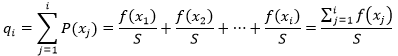
这就进一步得到了下表:

由于概率值是四舍五入,因此最后一个个体的概率分布值不是1,在选择的过程中多少会有一点吃亏。
接下来将所有qi映射到一个数轴上,每一段都表示一个个体:
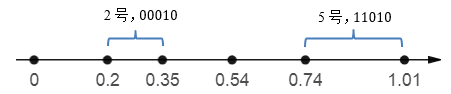
最后让小球在轮盘上转动。用一个区间在[0,1]的随机数r模拟这个小球,r将落在数轴的某一点上。若r≤q1,则第1个个体被选中;若qk-1≤r≤qk (2≤k≤n)则第k个个体选中。很明显,在两个相邻个体间,概率分布值相差越悬殊,后面的个体被选中的概率越大。图7.9中,r落在0.74和1.01之间的概率最大,因此5号个体最容易被选中;反之,2号个体最容易落选。反复迭代n次后,便得到了下一代种群,它们中会存在某些重复的个体,种群大小和上一代一致。
1 def pop_fitness(population): 2 ''' 计算种群中每个个体的适应度 ''' 3 return [fitness_fun(code) for code in population] 4 5 def selection_roulette(population): 6 ''' 7 轮盘赌选择算法 8 :param population: 种群 9 :return: 下一代种群 10 ''' 11 f_list = pop_fitness(population) # 每个个体的适应度 12 f_sum = [] # 第i个元素表示前i个体的适应度之和 13 for i in range(POPULATION_SIZE): 14 if i == 0: 15 f_sum.append(f_list[i]) 16 else: 17 f_sum.append(f_sum[i - 1] + f_list[i]) 18 S = sum(f_list) # 种群的总适应度 19 q = [f / S for f in f_sum] # 每个个体的概率分布 20 21 pop_next = [] # 下一代种群 22 for i in range(POPULATION_SIZE): 23 r = random.random() # 在[0,1]区间内产生一个均匀分布的随机数r 24 if r <= q[0]: # 若 r <= q0,则第1个个体被选中 25 pop_next.append(population[0]) 26 for k in range(1, POPULATION_SIZE): 27 if q[k - 1] < r <= q[k]: # 若q[k - 1] < r <= q[k],则第k个个体被选中 28 pop_next.append(population[k]) 29 break 30 return pop_next
一种可能的新种群是['11010', '01100', '11010', '00010', '10010'],可以看到,5号被选中了2次,1号、2号、4号各被选中1次,3号在生存竞争中惨遭淘汰。
2. 精英保留法
轮盘赌选择易于理解,但在后续的交叉配对中,很可能把较好的基因代码破坏掉,这就丧失了累积优良基因的目的,从而增加算法的迭代次数,延长算法的收敛时间。精英保留法避免了这个缺点,它会把种群在进化过程中出现的精英群体不进行配对交叉而直接复制到下一代,从而保证了优良的基因代码不会被破坏:
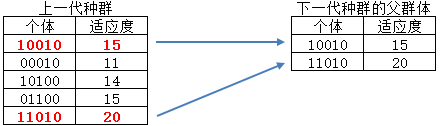
1 def selection_elitism(population): 2 ''' 精英选择策略''' 3 # 按适应度从大到小排序 4 pop_parents = sorted(population, key=lambda x: fitness_fun(x), reverse=True) 5 # 选择种群中适应度最高的40%作为精英 6 return pop_parents[0: int(POPULATION_SIZE * 0.4)]
在精英保留法中,通过交叉环节使下一代种群中的个体数量与上一代保持一致。精英保留法不给平庸的个体留一点活路,极端情况下,某些精英会从初代一直存活到算法结束,这可能使算法最终陷入局部最优解,可以说,精英保留法的缺点正是轮盘赌法的优点。
3. 锦标赛法
锦标赛法从种群中抽取一定数量的个体,让它们在锦标赛中进行竞争,其中胜出的个体进入下一代种群。重复该操作,直到新的种群规模达到原来的种群规模。每次参加锦标赛的个体数量称为锦标赛的“元”,通常使用二元锦标赛法。
1 def selection_tournament(population): 2 '''锦标赛选择策略''' 3 pop_next = [] # 下一代种群 4 for i in range(POPULATION_SIZE): 5 tour_list = random.choices(population, k=2) # 二元锦标赛 6 winner = max(tour_list, key=lambda x: fitness_fun(x)) 7 pop_next.append(winner) 8 return pop_next
在锦标赛法中,每个个体都有与其它实力相当的个体竞争的机会,即使最差的个体,也可能匹配到自己作为竞争对手,因此锦标赛法保留了轮盘赌法的优点,不易陷入局部最优解。同时,由于锦标赛法还具有较低的复杂度、易并行化处理,并且不需要对所有的适应度值进行排序,因此锦标赛法成为遗传算法中最流行的选择策略
交叉
交叉又称配对或重组,是指把两个父代个体的部分基因编码加以交换、重组而生成新个体的操作,其目的是保证种群的稳定性,使种群朝着最优解的方向进化。常用的交叉策略有单点交叉和两点交叉等。
1. 单点交叉
单点交叉又称一点交叉,它在个体基因序列中随机设置一个交叉点,然后随机选择两个个体做为父代个体,相互交换它们交叉点后面的那部分基因块,从而产生两个新的个体:

1 def crossover_onepoint(population): 2 ''' 单点交叉 ''' 3 pop_new = [] # 新种群 4 code_len = len(population[0]) # 基因编码的长度 5 for i in range(POPULATION_SIZE): 6 p = random.randint(1, code_len - 1) # 随机选择一个交叉点 7 r_list = random.choices(population, k=2) # 选择两个随机的个体 8 pop_new.append(r_list[0][0:p] + r_list[1][p:]) 9 return pop_new
2. 两点交叉
两点交叉又称局部交叉,它在个体基因序列中随机设置两个交叉点,然后随机选择两个个体做为父代个体,相互交换它们交叉点之间的那部分基因块,从而产生两个新的个体:

def crossover_twopoint(population): pop_new = [] # 新种群 code_len = len(population[0]) # 基因编码的长度 for i in range(POPULATION_SIZE): # 选择两个随机的交叉点 p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1) if p1 > p2: p1, p2 = p2, p1 r_list = random.choices(population, k=2) # 选择两个随机的个体 pop_new.append(r_list[0][0:p1] + r_list[1][p1:p2] + r_list[0][p2:]) return pop_new
交叉算法需要与基因编码配配合,在后续的示例中,我们将看到一些配合方案,同时也将看到其它的交叉策略。
变异
变异在遗传算法中只是用来产生新个体的辅助手段,它会改变个体的某一部分基因编码。和生物中的基因突变一样,变异算法的变异率应该控制在较低的频率。作为交叉运算的补充算法,变异对新种群的影响应该远小于交叉。常用的变异算法有单点变异和均匀变异。
1. 单点变异
单点变异较为简单,它在随机个体的基因编码中随机选取一个进行改变:
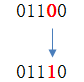
1 def mutation_onepoint(population): 2 '''单点变异''' 3 code_len = len(population[0]) # 基因编码的长度 4 mp = 0.2 # 变异率 5 for i, r in enumerate(population): 6 if random.random() < mp: 7 p = random.randint(0, code_len - 1) # 随机变异点 8 population[i] = r[0:p] + str(int(r[p]) ^ 1) + r[p + 1:]
变异操作直接修改了种群中的个体,并用“异或”操作模拟了变异,如果变异点的编码是1,那么变异后该点变为0;如果变异点的编码是0,那么变异后该点变为1。
2. 均匀变异
均匀变异又称一致性变异,它与单点变异类似,不同之处在于,均匀变异中随机个体的每一位基因代码都会随机发生变异。
1 def mutation_uniform(population): 2 ''' 多点变异 ''' 3 code_len = len(population[0]) # 基因编码的长度 4 mp = 0.2 # 变异率 5 for i, r in enumerate(population): 6 r_list = list(r) # 将个体的基因编码转换成列表 7 for p in range(code_len): # 遍历个体的每一位 8 if random.random() < mp: 9 r_list[p] = str(int(r_list[p]) ^ 1) 10 population[i] = ''.join(r_list)
python对于字符串的操作要比c或java笨拙一些,你可以用列表代替字符串表示基因编码。
这就是遗传算法
现在已经完成了所有铺垫,可以编写遗传算法的主体代码:
1 def ga(selection_fun=selection_tournament, crossover_fun=crossover_onepoint, 2 mutation_fun=mutation_onepoint): 3 ''' 遗传算法 4 :param selection_fun: 种群选择策略, 默认锦标赛策略 5 :param crossover_fun: 交叉策略,默认单点交叉 6 :param mutation_fun: 变异策略,默认单点变异 7 :return: 最优个体 8 ''' 9 population = init_population() # 构建初始化种群 10 sum_fitness = sum(pop_fitness(population)) # 种群的总适应度 11 i = 0 12 while i < 15: # 如果连续15代没有改进,结束算法 13 pop_next = selection_fun(population) # 选择种群 14 pop_new = crossover_fun(pop_next) # 交叉 15 mutation_fun(pop_new) # 变异 16 sum_fitness_new = sum(pop_fitness(pop_new)) # 新种群的总适应度 17 if sum_fitness < sum_fitness_new: 18 sum_fitness = sum_fitness_new 19 i = 0 20 else: 21 i += 1 22 population = pop_new 23 # 按适应度值从大到小排序 24 population = sorted(population, key=lambda x: fitness_fun(x), reverse=True) 25 # 返回最优的个体 26 return population[0] 27 28 if __name__ == '__main__': 29 best = ga() 30 print_solution(best)
这里用种群的总适应度作为评判标准,如果下一代的总适应度高于上一代,说明进化出了更强的下一代;当连续5代没有产生更强的后代时,结束算法。一种可能的运行结果:

交叉和变异并不一定都要执行,可以让种群中的大部分个体通过交叉产生,另一小部分通过变异产生。
遗传算法是否能够找到最优解,和初始种群、适应度评估函数、种群选择策略、交叉策略、变异策略、终止条件都有关系,每次运行的结果都可能不同,但总体上能够得到一个较为满意的解。在实际应用中,我们可以选择不同的参数多次运行,挑选最好的一个作为最终结果。
完整代码:
1 import random 2 3 GOODS_LIST = [('A', 3, 4), ('B', 4, 5), ('C', 7, 10), ('D', 8, 11), ('E', 9, 13)] 4 V_BAG = 20 # 背包的容量 5 POPULATION_SIZE = 5 # 种群数量 6 7 def print_solution(code): 8 ''' 9 打印解决方案 10 :param code: 二进制基因编码 11 ''' 12 size_sum, value_sum, = 0, 0 13 for i, x in enumerate(code): 14 if x == '1': 15 gtype, size, value = GOODS_LIST[i] 16 print('\t{0}\t体积:{1}\t价值:{2}'.format(gtype, size, value)) 17 size_sum += size 18 value_sum += value 19 print('\t背包内的物品总体积:{0},\t总价值:{1}'.format(size_sum, value_sum)) 20 21 def init_population(): 22 ''' 构造初始种群 ''' 23 population = [] 24 code_len = len(GOODS_LIST) # 编码长度 25 for i in range(POPULATION_SIZE): 26 population.append(''.join(random.choices(['0', '1'], k=code_len))) 27 return population 28 29 def fitness_fun(code): 30 ''' 31 适应度评估 32 :param code: 二进制基因编码 33 :return: 适应度评估值 34 ''' 35 size_sum, sum_value = 0, 0 # 物品的总体积,物品的总价值 36 for i, x in enumerate(code): 37 if x == '1': 38 _, size, value = GOODS_LIST[i] 39 size_sum += size 40 sum_value += value 41 if size_sum > V_BAG: # 背包被撑爆时,适应度为0 42 sum_value = 0 43 break 44 return sum_value 45 46 def pop_fitness(population): 47 ''' 计算种群中每个个体的适应度 ''' 48 return [fitness_fun(code) for code in population] 49 50 def selection_roulette(population): 51 ''' 52 轮盘赌选择算法 53 :param population: 种群 54 :return: 下一代种群 55 ''' 56 f_list = pop_fitness(population) # 每个个体的适应度 57 f_sum = [] # 第i个元素表示前i个体的适应度之和 58 for i in range(POPULATION_SIZE): 59 if i == 0: 60 f_sum.append(f_list[i]) 61 else: 62 f_sum.append(f_sum[i - 1] + f_list[i]) 63 S = sum(f_list) # 种群的总适应度 64 q = [f / S for f in f_sum] # 每个个体的概率分布 65 66 pop_next = [] # 下一代种群 67 for i in range(POPULATION_SIZE): 68 r = random.random() # 在[0,1]区间内产生一个均匀分布的随机数r 69 if r <= q[0]: # 若 r <= q0,则第1个个体被选中 70 pop_next.append(population[0]) 71 for k in range(1, POPULATION_SIZE): 72 if q[k - 1] < r <= q[k]: # 若q[k - 1] < r <= q[k],则第k个个体被选中 73 pop_next.append(population[k]) 74 break 75 return pop_next 76 77 def selection_elitism(population): 78 ''' 精英选择策略''' 79 # 按适应度从大到小排序 80 pop_parents = sorted(population, key=lambda x: fitness_fun(x), reverse=True) 81 # 选择种群中适应度最高的40%作为精英 82 return pop_parents[0: int(POPULATION_SIZE * 0.4)] 83 84 def selection_tournament(population): 85 '''锦标赛选择策略''' 86 pop_next = [] # 下一代种群 87 for i in range(POPULATION_SIZE): 88 tour_list = random.choices(population, k=2) # 二元锦标赛 89 winner = max(tour_list, key=lambda x: fitness_fun(x)) 90 pop_next.append(winner) 91 return pop_next 92 93 def crossover_onepoint(population): 94 ''' 单点交叉 ''' 95 pop_new = [] # 新种群 96 code_len = len(population[0]) # 基因编码的长度 97 for i in range(POPULATION_SIZE): 98 p = random.randint(1, code_len - 1) # 随机选择一个交叉点 99 r_list = random.choices(population, k=2) # 选择两个随机的个体 100 pop_new.append(r_list[0][0:p] + r_list[1][p:]) 101 return pop_new 102 103 def crossover_twopoint(population): 104 pop_new = [] # 新种群 105 code_len = len(population[0]) # 基因编码的长度 106 for i in range(POPULATION_SIZE): 107 # 选择两个随机的交叉点 108 p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1) 109 if p1 > p2: 110 p1, p2 = p2, p1 111 r_list = random.choices(population, k=2) # 选择两个随机的个体 112 pop_new.append(r_list[0][0:p1] + r_list[1][p1:p2] + r_list[0][p2:]) 113 return pop_new 114 115 def mutation_onepoint(population): 116 '''单点变异''' 117 code_len = len(population[0]) # 基因编码的长度 118 mp = 0.2 # 变异率 119 for i, r in enumerate(population): 120 if random.random() < mp: 121 p = random.randint(0, code_len - 1) # 随机变异点 122 population[i] = r[0:p] + str(int(r[p]) ^ 1) + r[p + 1:] 123 124 def mutation_uniform(population): 125 ''' 多点变异 ''' 126 code_len = len(population[0]) # 基因编码的长度 127 mp = 0.2 # 变异率 128 for i, r in enumerate(population): 129 r_list = list(r) # 将个体的基因编码转换成列表 130 for p in range(code_len): # 遍历个体的每一位 131 if random.random() < mp: 132 r_list[p] = str(int(r_list[p]) ^ 1) 133 population[i] = ''.join(r_list) 134 135 def ga(selection_fun=selection_tournament, crossover_fun=crossover_onepoint, 136 mutation_fun=mutation_onepoint): 137 ''' 遗传算法 138 :param selection_fun: 种群选择策略, 默认锦标赛策略 139 :param crossover_fun: 交叉策略,默认单点交叉 140 :param mutation_fun: 变异策略,默认单点变异 141 :return: 最优个体 142 ''' 143 population = init_population() # 构建初始化种群 144 sum_fitness = sum(pop_fitness(population)) # 种群的总适应度 145 i = 0 146 while i < 15: # 如果连续15代没有改进,结束算法 147 pop_next = selection_fun(population) # 选择种群 148 pop_new = crossover_fun(pop_next) # 交叉 149 mutation_fun(pop_new) # 变异 150 sum_fitness_new = sum(pop_fitness(pop_new)) # 新种群的总适应度 151 if sum_fitness < sum_fitness_new: 152 sum_fitness = sum_fitness_new 153 i = 0 154 else: 155 i += 1 156 population = pop_new 157 # 按适应度值从大到小排序 158 population = sorted(population, key=lambda x: fitness_fun(x), reverse=True) 159 # 返回最优的个体 160 return population[0] 161 162 if __name__ == '__main__': 163 best = ga() 164 print_solution(best)
在下一章中,我们将尝试用遗传算法进行上一章的宿舍分配工作,同时展示不同于二进制的编码方案和另一些能够与之配合的交叉策略。
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号