退而求其次(1)——随机法
又是一年开学季，来自全国各地的新生聚集到校园里。
入学的第一件事是分配宿舍。为了提升学生住宿的满意度，今年学校特意就学生的一些信息进行了调查，并要求宿管员根据问卷对宿舍进行最合理的分配，力争全体新生都对分配结果满意，问卷如下：
一共收到了数百份问卷，在宿管员的桌子上堆了厚厚的一摞。为了叙述方便，我们把问题缩小，假设只收到了16张问卷，形成了统计数据：
这16个新生被分到4个宿舍。宿管员在尝试分配的时候发现了一些问题，比如瑞萌萌和何蔚蓝两人，她们属于同一专业、同一班级，有相同的爱好，然而两人来自祖国的南北两地，距离相差了3000公里，这注定两人的生活习惯有诸多不同，而且同样是普通话，吉林人有比较重的东北口音，广州人并不一定能听懂。何蔚蓝最在意的专业相同，看起来瑞萌萌是个不错的室友；瑞萌萌最在意的却是籍贯，她的理想室友是和她几乎处处不同的莫伊；但莫伊并不建议籍贯问题，她更想和专业相同的同学共处一室……这可难坏了宿管员。
宿管员拿着表格向计算机系的张老师求助，希望能借助计算机的力量处理这个复杂的问题。张老师很乐于帮助宿管员，爽快地接下了这个工作。
成本函数和数据预处理
张老师的方法是通过计分的方法计算同学们差异度，分数越高，两个同学的差异越大，同学对分配结果的抱怨就越大；最好的结果是0，表示同学们的习惯爱好等完全一致。差异度是通过一个函数计算的，这个函数称为成本函数。对于同一个宿舍的两种不同的分配方式来说，将全寝同学的成本累加，数值较小的一个就是整体满意度较高的。
在成本函数中，我们使用曼哈顿距离计算两个同学的差异度。计算前需要先对数据进行预处理，将所有非数值数据量化，样才能通过成本函数算出数值。统计表中有4个男同学，他们肯定要分在一起，至于是否满意就没人管了，需要确保满意度的是12个女同学。
调查问卷中一共有八个问题，每个问题可以看作向量中的一个维度，由于分配目标是女同学，因此可以先去掉性别这一维度；姓名维度充当了索引的作用，同样不参与运算。在剩下的六个维度中，“最在意”可以看作其它维度的权重，这样一来，需要进行数值转换的只剩下籍贯、专业、班级、起床时间、爱好五个维度。
我们使用一种简单的方式计算两个同学间的差异度：每一个维度的最大成本是5，最小是0，权重是1.5，这样两个同学间的最小差异是0；最大差异是二者的所有数据都不同，而且将权重加在了不同的维度上，差异值是5×3+5×1.5+5×1.5=30。来看看如何对每个维度进行数值化。
对于籍贯来说，我们简单的认为同一个省份的差异较小，因此只比较省份，用省份代码表示省份，两个省相同，差异是0，否则是5。
专业维度与籍贯类似，设计算机、数学、英语分别是1、2、3，相同专业的差异是0，否则是5。
我们注意到1班和2班都是计算机专业，两个班的同学会在一起上很多课程，因此1班和2班的距离更近一点，二者的距离是1，和其两班的距离是5。
起床最早的是琪琳和怜风，6:10就起床了，最晚的蔷薇7:30才起床。以20分钟为一个时间段，认为6:00~6:20属于同一时段，在此期间起床的同学差异度是0。6:00~7:30可以划分为5个时段，分别数值化为1~5。7:30和6:10间相差了4个时段，两个相邻时段间的差异是5÷4=1.2。
12个同学共有12种爱好，这种多才多艺也为计算带来的难度。一种简单的方式是，如果两个同学都有一个共同的爱好，二者就是零距离。此外我们也应该注意到，一些爱好虽然不同，但有很大程度相似性，比如书法和绘画，同属“四艺”，又都是和笔纸大交道，应该有更多的共性；同样，跑步和游泳都属于体育，也会有更多的共同语言。按照这个规则将12种爱好分成五类（这里不讨论分类是否恰当）：
读写类：读书、书法、绘画
体育类：跑步、游泳
音乐类：电子琴、舞蹈、唱歌
娱乐类：看电影、逛街、电子游戏
科技类：天文
大类之间的相异是5，同一大类下的小类间差异是2，具体的数值化：
蕾娜和琪琳都喜欢读书，她们的差异是0；鹤熙喜欢绘画，怜风喜欢书法，虽然爱好不同，但同属于都写类，她们的差异是2；喜欢天文的只有凉冰自己，没有任何人的爱好和她是同一类，因此她和所有人的差异都是5。
在数据预处理的过程中可能有很多更复杂的情况值得考虑，比如对于籍贯来说，辽宁和吉林的代码是21和22，二者都属于东三省，在生活习惯上较为相近；宁夏和新疆的代码是64和65，虽然同属于西北，但民风民俗都相去甚远。
现在可以把统计数据转换成纯数值数据：
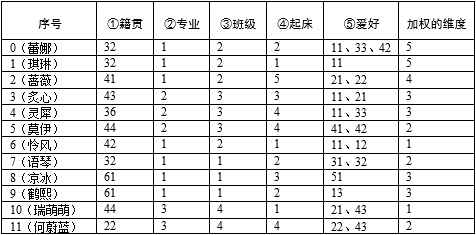
时间段划分的规则：6:01~6:20，6:21~6:40，6:41~7:00，7:01~7:20，7:21~7:40。
用列表存储统计数据和学生姓名：
# 学生调查表数据 STUDENTS = [ [32, 1, 2, 2, [11, 33, 42], 5], [32, 1, 2, 1, [11], 5], [41, 1, 2, 5, [21, 22], 4], [43, 2, 3, 3, [11, 21], 3], [36, 2, 3, 4, [11, 33], 3], [44, 2, 3, 4, [41, 42], 2], [42, 1, 2, 1, [11, 12], 1], [32, 1, 1, 2, [31, 32], 2], [61, 1, 1, 3, [51], 3], [61, 1, 1, 2, [13], 3], [44, 3, 4, 1, [21, 43], 1], [22, 3, 4, 4, [22, 43], 2] ] # 学生姓名 STUDENTS_NAME = ['蕾娜', '琪琳', '蔷薇', '炙心', '灵犀', '莫伊', '怜风', '语琴', '凉冰', '鹤熙', '瑞萌萌', '何蔚蓝'] DROM_COUNT = 3 # 宿舍数量 NUM_PER_DROM = 4 # 每个宿舍的人数
在上一章中我们已经见识过平面上的曼哈顿距离，其实各种距离的计算都可以扩展到多维数据，两个同学间的差异值如下：
MAX_COST = 5 # 同一维度间的最大成本 def cost_stu(stu_1, stu_2): ''' 以stu_1为主，计算stu_1与stu_2的差异 ''' cost = [] # 各维度的成本值（差异度） cost.append(cost_equal(stu_1[0], stu_2[0])) # 籍贯成本 cost.append(cost_equal(stu_1[1], stu_2[1])) # 专业成本 cost.append(cost_class(stu_1[2], stu_2[2], stu_1[1], stu_2[1])) # 班级成本 cost.append(cost_get_up(stu_1[3], stu_2[3])) # 起床成本 cost.append(cost_interest(stu_1[4], stu_2[4])) # 爱好成本 w_idx_1, w_idx_2 = stu_1[len(stu_1) - 1] - 1, stu_2[len(stu_2) - 1] - 1 # 权重序号 w_cost_1, w_cost_2 = cost[w_idx_1] * 1.5, cost[w_idx_2] * 1.5 # 加权处理 # 判断二者最在意的是否相同 if w_idx_1 == w_idx_1: cost[w_idx_1] = w_cost_1 + w_cost_2 else: cost[w_idx_1], cost[w_idx_2] = w_cost_1, w_cost_2 return sum(cost) def cost_equal(d_1, d_2): ''' 同质化比较成本 ''' return 0 if d_1 == d_2 else MAX_COST def cost_class(d_1, d_2, sub_1, sub_2): ''' 班级成本 ''' if d_1 == d_1: # 班级相同 return 0 elif sub_1 == sub_1: # 不同班级，同一专业 return 1 else: # 不同班级，不同专业 return MAX_COST def cost_get_up(d_1, d_2): ''' 起床成本 ''' return 1.2 * (d_2 - d_1) def cost_interest(d_1, d_2): ''' 爱好成本 ''' for t_1 in d_1: # 如果两个同学都有一个共同的爱好，二者就是零距离 if t_1 in d_2: return 0 obj_1 = t_1 // 10 # 爱好的“大类” # 如果两个同学都有一个共同的大类，二者距离是2 for t_2 in d_2: if obj_1 == t_2 // 10: return 2 return MAX_COST
在处理同学间差异的cost_stu()方法中，对于分别计算了stu_1最在意的加权值和 stu_2的加权值，这是因为需要同时考虑两个人的感受，避免出现“我喜欢你，但你不喜欢我”的情况。
一个宿舍的总成本需要考虑每个同学的满意度，相当于该宿舍四个同学间两两比对后得出的差异度之和。一个方案的总成本是将该方案中所有宿舍的成本累加：
def cost_fun(scheme): ''' 计算方案中每个宿舍的成本 :param scheme: 宿舍分配方案 :return: 宿舍总成本 ''' droms_cost = [] for drom in scheme: # 同一宿舍中的四个同学两两比对 d_cost = 0 d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[1]]) d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[2]]) d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[3]]) d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[2]]) d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[3]]) d_cost += cost_stu(STUDENTS[drom[2]], STUDENTS[drom[3]]) droms_cost.append(d_cost) diff_cost = max(droms_cost) - min(droms_cost) # 宿舍之间的贫富差 total_cost = sum(droms_cost) return total_cost
解空间的数量
第一个想到的方法是穷举法，只要把所有的宿舍分配情况都列出来，就可以成本排序，最终选取成本最低的一个最为满意度最高的方案。
分配方案有几种呢？首先在12个同学中任意挑选四个住在0号宿舍的，选择的同学的顺序与方案无关，一共会有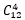
种分配方案；还剩下8个同学，1号宿舍的分配方案有
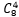种；最后的四个同学只能住进2号宿舍，有
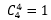种方案。
三个宿舍可以产生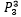
种不同的排列方式。假设是宿舍本身没有优劣之分，对于任意四个同学来说，住在宿舍1和宿舍2并不影响满意度，在这个前提下，解空间中解的数量是：
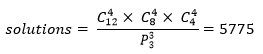
12个同学的分配就有这么多的方案，20个同学分配到5个宿舍，方案将增加到525525种；100个同学分到25个宿舍的方案就更多了：
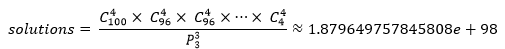
如果蛮力法穷举的话，直到毕业也算不出结果。
问题的难点
庞大的解空间使蛮力法通向了死路，贪心法又如何呢？
似乎很容易定义贪心策略，先把任意一个同学分到0号宿舍，然后再选择与这个同学最相近的第二个同学，一共需要进行11次成本计算。第三个同学需要和前两个同学都进行比对，这样才能保证新加入的同学与原来的同学都能较为融洽地相处，需要进行2×10次运算；同理，第四个同学需要考虑前三个同学。每个宿舍的算数量是：
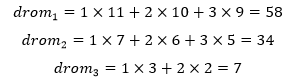
这比蛮力法强多了。
然而看似快速的贪心法虽然能使总成本最低，但是会引起另一个问题——贫富分化严重，最先分配的宿舍满意度最高，最后一个宿舍可能人人不满，这当然不是学校的初衷。看来在计算总成本时，还要额外考虑“不均”的问题，因此需要修改成本函数：
def cost_fun(solution): ''' 计算方案中每个宿舍的成本 :param solution: 宿舍分配方案 :return: 宿舍总成本和每个宿舍的成本 ''' droms_cost = [] for drom in solution: # 同一宿舍中的四个同学两两比对 d_cost = 0 d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[1]]) d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[2]]) d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[3]]) d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[2]]) d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[3]]) d_cost += cost_stu(STUDENTS[drom[2]], STUDENTS[drom[3]]) droms_cost.append(d_cost) diff_cost = max(droms_cost) - min(droms_cost) # 宿舍之间的贫富差 total_cost = sum(droms_cost) + diff_cost * DROM_COUNT # 该方案的总成本 return total_cost, droms_cost
贫富差是用满意度最低的成本值减去满意度最高的成本值，在此基础上乘以权重（这里权重是宿舍总数），表示贫富差异的成本。
随机法
在庞大的解空间中找出最好的方案实在是不容易，而且无论如何分配，总会有人不满，这时候不妨退一步，选择一个较好的解。
一个简单的优化方法是“随机法”，用抽签的方式决定入住那个宿舍，并把抽签的结果记录下来，反复抽取若干次后，选择结果最好的那个最为最终方案，代码如下：
def random_optimize(): ''' 随机法 :return: 最佳方案，方案的总成本，方案中每个宿舍的成本 ''' n = len(STUDENTS_NAME) best = None # 最佳方案 best_total_cost, best_droms_cost = 9999999, [] # 最佳方案的宿舍成本和总成本 # 随机分配1000次 for t in range(1000): solution = [] stu_list = base_data.upset() # 将学生分配到宿舍中 for i in range(0, n, NUM_PER_DROM): solution.append(stu_list[i:i + NUM_PER_DROM]) total_cost, droms_cost = cost_fun(solution) # 计算该方案的成本 if total_cost < best_total_cost: best = solution best_total_cost, best_droms_cost = total_cost, droms_cost return best, best_total_cost, best_droms_cost best, best_total_cost, best_droms_cost = random_optimize() display(best, best_total_cost, best_droms_cost)
random_optimize()将学生随机分配了1000次，选择1000种方案中成本值最低的一个。一种可能的运行结果：
其实随机法很常见，比如调查国家的平均工资时，并不会把每个人都计算在内，而是随机选择一部分，认为这个结果接近于真实的平均。由于计算结果看起来与直观感受不同，并不那么“最优”，因此随机法经常被诟病，经常被调侃“拖了后退”。
另一个被诟病的原因是“欠缺技术含量”，以至于并不像一个正统的解决方案。种观点也许可以用一个不太恰当的例子反驳这：大多数使用过Windows系统的人都经历过“蓝屏”，其中Win98的蓝屏频率最高。到了Win7时代，虽然问题已经得到了极大的改善，但仍有某些时候会出现蓝屏。在众多导致蓝屏的问题中，有一个错误码是“1131 0x046B”，表示“发现了潜在的死锁条件”。死锁是多线程中的难题，由于它的不可重现性，调试起来极其困难，只能凭借开发人员的经验，微软对待这个问题的态度是“不做处理”。这令很多人感到气愤。其实“不做处理”正是解决死锁问题的方案之一，当解决问题的代价远远大于问题本身的时候，“不做处理”是一个明智的选择——与其耗费大量资源处理一个不见得能解决的问题，还不如就让它蓝屏，反正出现概率很低，重启一次算了。其实我们这生活中也经常使用“不做处理”的方案，当你碰到困难时，是选择迎难而上，还是选择退缩？想必大多数人都曾经退缩过，此时你正是使用了“欠缺技术含量”的解决方案。
这并非为随机法正名，这个不够好的方法经常是作为“标杆”使用，后续章节中我们将看到更强的随机化算法。
作者：我是8位的
