密码疑云 (2)——RSA加密机制需要的数学知识
在公钥密码体制提出不久,人们就找到其中的三种,其中最著名的当属RSA体制。RSA是一种非对称加密体制,在公开密钥加密和电子商业中被广泛使用。RSA是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院工作,RSA就是他们三人姓氏开头字母拼在一起组成的。

RSA背后的原理是一个数论理论——将两个大素数(比如1024位的素数)相乘很容易,但是想要对它们的乘积进行素因子分解(重新分解成原来的两个素数的乘积)却及其困难。在理解RSA之前还需要知道一些数学概念。
公约数定理和线性不定方程
公约数存在两个定理,如果d=GCD(a,b)则:
1. 存在整数x,y,使得d=ax+by,当然,x,y用不着全是正整数(贝祖定理);
2. 如果c是a,b的另一个公约数,则c|d
定理2还产生了一个推论:GCD(a,b)是a,b的线性组合{ax+by}中的最小正元素。
根据公约数定理可以给出线性不定方程的定义:对于任意整数a,b,c,型如ax+by=c的方程称为线性不定方程,“线性”表示方程的未知数次数是一次,“不定” 表示未知数的个数多于方程的个数。如果c= GCD(a,b),则方程存在一组整数解;如果c是GCD(a,b)的整数倍,方程存在多组整数解;否则方程无整数解。
通常使用欧几里德算法求解线性方程组ax+by=GCD(a,b)。欧几里德算法通过辗转关系求得两个数的最大公约数:
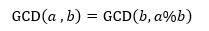
不断迭代,直到a%b=0为止:
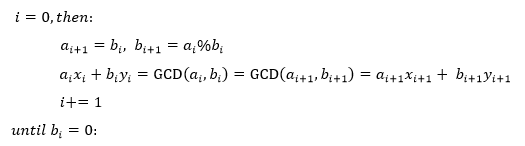
下标表示迭代次数,原方程是第0次迭代。
欧几里德算法(辗转相除)可参考整数的故事(2)——辗转相除与更相减损
最后一次迭代(第n+1次迭代)时,an%bn=0:

其中的一组特解是xn+1=1,yn+1=0,虽然这组解并不是关于x0和y0的,但可以通过它反向推出原方程的解。
在Python中,a%b==a-(a//b)*b代入①中可以得到xn=1,yn与xn+1=1,yn+1的关系:
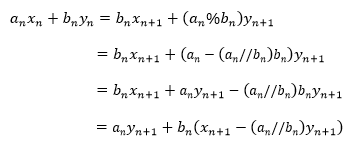
当xn=1,yn与xn+1=1,yn+1 满足下面关系时,上式是恒等式:
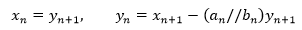
恒等式(identities)无论变量如何取值,等式永远成立。
这样就可以由xn+1和yn+1推出xn和yn,不断向前递推,最终可以求得x0和y0。下面的代码可求得原方程的解,被称为扩展欧几里德算法:
def extEculid(a, b): '''扩展欧几里德算法 计算 ax-by = GCD(a, b)的特解''' if b == 0: x, y = 1, 0 return x,y x, y = extEculid(b, a % b) return y, x - (a // b) * y if __name__ == '__main__': print('5x + 10y = 5', '=>', extEculid(5, 10)) print('5x + 11y = 1', '=>', extEculid(5, 11)) print('16x + 24y = 8', '=>', extEculid(16, 24)) print('72x + 57y = 3', '=>', extEculid(72, 57))
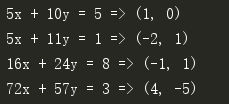
作为一种最简情况,对于ax+by=1来说,如果GCD(a,b) = 1,方程有唯一解。这是由ax+by=GCD(a,b)推导而来的:

由于d是a和b的最大公约数,所以a/d和b/d一定是整数,且它们之间不会再有其它约数(否则d就不是a和b的最大公约数):
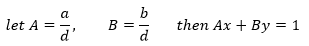
重新命名系数,用a,b代替A,B就可以得出结论。
如果在原方程中c是GCD(a,b)的整数倍,方程组有多组解,这些解是什么呢?
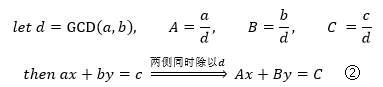
由于d已经是a,b的最大公约数,所以A,B不再有其它的约数,A,B互质于是不定方程③有唯一解:
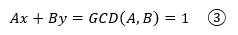
根据扩展欧几里德算法可以计算出它的唯一解,设这组解是x0,y0,将解代入③:
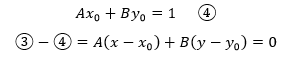
由A,B互质,因此x-x0定有因子B,y-y0一定有因子A,由此可以得到不定方程的通解:
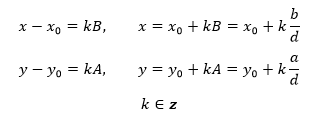
满足方程的解有无穷多个,在实际问题中我们常常只要求其最小正整数解。如果不考虑y的取值, 的最小正整数解就是 x0+kb/d>0时的最小值(注意是 x0+kb/d的最小值,不是x0的最小值)。
青蛙约会
一个圆形围墙下有两只青蛙A和B想要约会,它们的位置分别是x和y。它们高兴地出发了,但是出发前忘记了通知对方朝哪个方向前进。现在A、B同时沿着围墙的同一方向跳跃,A每次跳m,B每次跳n,场地的周长是L。假设两只青蛙跳跃一次的耗时相同,它们落在同一点视为相遇,那么它们经过几次跳跃才能相遇?
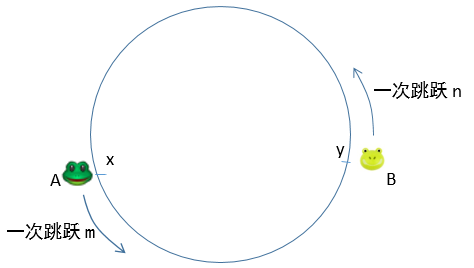
青蛙约会成功的第一个前提是m≠n,否则它们会永远跳下去。假设x和y相距很近,并且A跳跃的比较快,如果能够相遇,那么A一定会比B至少多跳一圈,也就是运动会上常说的“扣圈”。当然了,在A马上要追上B时,如果下一跳又正好跳到了B的前面,那么这一圈就白扣了,需要重新追赶。设它们经过t次跳跃能够相遇,相遇时A比B多跳了k圈,可以写出下面的式子:
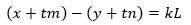
其中x,y,m,n,L是已知的,t,k是未知的,上式可以进一步转化为:
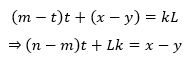
这和线性不定方程ax+by=c的形式一致。如果方程有整数解,那么x-y一定是GCD(n-m, L)的整数倍,此时可以根据扩展欧几里德算法求出线性方程的最小解。
同余、同余方程和乘法逆元
a和b是两个整数,如果它们的差a-b能够被另一个整数n整除,则称a,b对于模n同余,记作a≡b (mod n),读作a与b关于模n同余(a is congruent to b mod n)。a≡b (mod n)的等价形式是当且仅当n|(a-b),
a,b对于模可理解为a-b=kn,k是任意整数。当a≡0 (mod n)时,则n|a。
例如:

数学中被重用的符号很多,同余符号“≡”就是其中的一个。在几何中,“≡”也表示全等符号,△ABC和△A’B’C’全等,记作△ABC≡△A’B’C’,等同于△ABC≌△A’B’C’符号。在函数中,“≡”可以表示“恒等”,函数f(x)≡n表示该函数的值始终为n,与x的值无关。
同余问题很常见,例如从今天起计算n天和m天后是否是星期中的同一天?答案是当n≡m (mod 7)时。类似的例子还有很多,例如平面上位于同一顶点的两个线段,当各自朝同一方向旋转了n和m,当n≡m(mod 360°)时将重合;钟表上的时针从当前位置经过了n小时和m小时,当n≡m (mod 12)时会到达同一位置。
同余符号“≡”比等号“=”多了一横,它与等号具有的性质类似,允许两边同时加上或减去同一个量,或同时乘以一个常数,对于a≡b (mod n),当c是整数时:
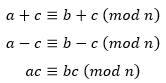
我们把型如ax≡b (mod n)的方程称为线性同余方程。在数论中,线性同余方程是最基本的同余方程,“线性”表示方程的未知数次数是一次。
同余方程的解有三种情况,只有当GDD(a, n)|b时,方程有解,例如:
1. 无解,例如2x≡1 (mod 4);
2. 有唯一解,例如2x≡1 (mod 5);
3. 有无数解,例如2x≡0 (mod 4);
原方程是ax≡b (mod n),则原方程的等价形式是:
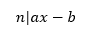
设y是一个指定的整数,则n能整除ax-b意味着:
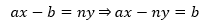
这就把同余方程转换成了线性不定方程ax+by=c的形式,可以用扩展欧几里德算法求解。当GCD(a, n)=b时,ax≡b (mod n)有唯一整数解。类似地,当b是GCD(a,n)的倍数时,同余方程有多组解。
作为最简情况,当ax-ny=1时,如果GCD(a,n)=1,则方程有唯一整数解,这个整数解就称为a在模n上的乘法逆元,记作a-1:
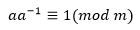
欧拉函数
对正整数n,欧拉函数(Euler's totient function)是小于n的正整数中与n互质的正整数的个数,用φ(n)表示。欧拉函数又称为φ函数、欧拉商数等,φ(n)的值被称为n的欧拉数。规定φ(1)=1。例如,在小于8的正整数中,1,3,5,7都与8互质,因此φ(8)=4,φ(8)是一个欧拉函数,它的值等于4,4是8的欧拉数。
当n是素数时,φ(n)=n-1,因为所有小于n的数都和n互素。
注:当年欧拉认可1是素数,所以在欧拉函数中1也被加了上去。下文在讨论欧拉函数时都把1视为素数。
欧拉函数有一个性质,如果n可以分解为两个互素正整数p和q的乘积,那么n的欧拉函数就是p和q的欧拉函数的乘积,即:
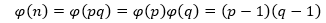
例如,小于12的正整数中与12互质的有1,5,7,11,所以φ(12)=4。12可以分解为两个互素的数3和4的乘积,因此:
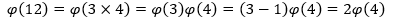
这里也许会产生一个冲动,把φ(4)继续写成φ(4)= 4-1,这是错误的,φ(n)=n-1的前提是n是素数,因此φ(4)≠4-1。另一个冲动是写成φ(4)= φ(2) φ(2),这也是错误的,两个数互素的前提是它们的最大公约数是1,GCD(2,2)=2,因此2和2并不互素。
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号