算法分析(3)——冒泡排序真的慢吗?
在初学编程的时候,曾经有两个问题让我感到迷惑,第一个是利用中间变量交换另外两个变量,另一个就是冒泡排序。但是后来发现,冒泡排序几乎是所有排序算法中最简并且容易实现的,实际上许多人了解的第一个排序算法就是冒泡排序。总有人说:“日本人说英语口音太重,听不懂”,就好像没有口音能听得懂一样,人们也经常说冒泡排序效率低下,事实真的如此吗?
排序的关注点
在分析排序之前了解一下排序算法的关注点是有必要的。
首先是排序的种类,根据待排序文件涉及的存储器,可将排序方法分为两大类,内部排序和外部排序。内部排序指待排序的文件可以全部放在内存中。内存的访问速度大约是磁盘的25万倍,如果可以的话,我们当然希望所有排序都是在内存中完成。但对于大文件或大数据集来说,内存并不能容纳全部记录,在排序过程中还需对外存进行访问,这就是外部排序。我们一般提到的排序算法,比如冒泡排序、希尔排序、快速排序等都是内部排序。
另一个关注点是稳定性。很多带排序的记录依赖于关键字,而这些关键字可能相同,比如对一个班级的考试成绩排序,学生的分数就是关键字,学生姓名是关键字对应的信息:

其中赵信和刘闯的分数相同,杜蔷薇和琪琳的分数相同,如果某一种排序算法结果不改变关键字相同的记录的顺序,则这个排序是稳定的,否则就是不稳定的:
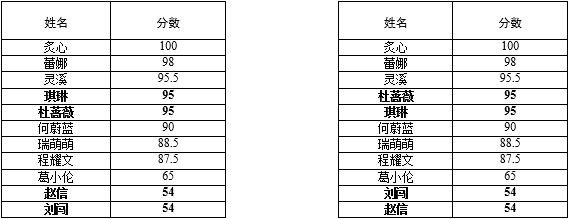
在稳定排序中,琪琳仍排在杜蔷薇之前,赵信也扔排在刘闯之前,而不稳定排序只关心关键字的顺序,至于关键字对应的记录是否还会保持原来的顺序则并不在考虑范围内。复杂的算法很少先天带有稳定性(比如快速排序),需要付出额外的时间或空间才能达到稳定的目的。
最后一个关注的是数据结构,大体上由数组和链表可供选择。有时候,排序对于数据结构相当敏感,一些对链表有优越表现的算法未必对数组适用。
我们把注意力集中在内部排序上,仅对排序的性能进行分析,而不关注算法的稳定性和数据结构。
抽象表达
抽象表达是面向对象的基本思路,它可以使算法的内部操作不依赖于具体的数据类型,因此我们同样基于抽象表达分析算法。下面的代码定义了数据类型的抽象结构:
class Item: k = None # 关键字 v = None # 关键字对应的值 def less(self, item): ''' :return: k是否小于item的关键字 ''' pass def get_k(self): return self.k def get_v(self): return self.v
其中less方法用于比较两个元素关键字的大小,如果当前元素小于参数中的元素,返回True。这种抽象是有意义的,对于字符串关键字的比较肯定比数字关键字更耗时,如果关键字的比较还需要依赖网络等不确定因素,程序的总体运行时间就更没谱了,抽象的表达便于我们排除干扰,聚焦于算法本身。下面的是学生分数的Item实现:
class Score(Item): def __init__(self, score:float, name:str): self.k = score self.v = name def less(self, item): return self.k < item.get_k() def visit(self): print('{0}, 分数={1}'.format(self.get_v(), self.get_k()))
冒泡排序
准备工作已经就绪,开始冒泡:
def create_data(): s1 = Score(65, '葛小伦') s2 = Score(54, '赵信') s3 = Score(54, '刘闯') s4 = Score(95, '琪琳') s5 = Score(98, '蕾娜') s6 = Score(95, '杜蔷薇') s7 = Score(87.5, '程耀文') s8 = Score(88.5, '瑞萌萌') s9 = Score(90, '何蔚蓝') s10 = Score(100, '炙心') s11 = Score(95.5, '灵溪') return [s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11] def exchange(item_list, i, j): ''' 交换item_list中的第i个和第j个数据 ''' item_list[i], item_list[j] = item_list[j], item_list[i] def bubble_sort(item_list): ''' 冒泡排序 ''' n = len(item_list) for i in range(0, n): for j in range(i + 1, n): if item_list[i].less(item_list[j]): exchange(item_list, i, j) if __name__ == '__main__': item_list = create_data() bubble_sort(item_list) for item in item_list: item.visit()
这里把交换方法单独抽取出来是有意义的,如果数据较多,可以在exchange中添加一个计数器,这样就可以了解一共交换了多少次,从而知道数据是否大致有序,而且exchange同样对于算法屏蔽了交换细节。打印结果如下:
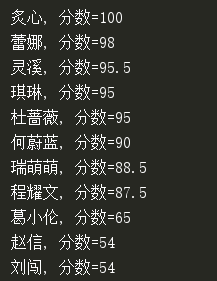
观察冒泡排序的两层循环,外层循环需要n轮迭代,内层循环的迭代次数呈递减趋势。可以看出,当i=0时,内层循环迭代n-1次;当i=1时,内层循环迭代n-2次……i=n-1,内存循环迭代0次,因此内层循环的总迭代次数是:
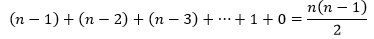
每次内层迭代都会把一个数据放置到位,这里涉及到比较和数据交换。对于一个复杂度是N的问题,如果数据已经是有序的,冒泡排序的比较次数是内层迭代总次数,而交换次数是0。我们用C和M分别表示比较次数和交换次数:

如果数据是完全逆序的,那么每一次比较都伴随着数据交换,这种情况下:

可以看出,冒泡排序的比较次数不受数据的影响,有影响的是交换次数,综合来看,冒泡排序的时间复杂度是:
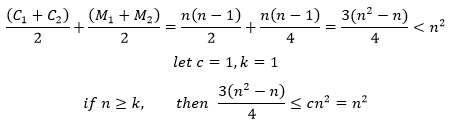
因此,在使用O表示法时,可以认为冒泡排序的时间复杂度是O(n2),无论文件是否有序。
最后的结论
对于一个算法来说,时间复杂度是 O(n2)不是个太好的评价,更何况在任何时候都是 O(n2),这足以在大多数时候都让人觉得冒泡排序效率低下。真的是这样吗?从算法分析的结果来说,是的;但是从实际应用来说就未必了。作为一种基本排序,冒泡排序算法总是适合于几百个以内的较小数据集,而一个复杂的算法中处理小数据的考校可能会更慢。这并不算骇人听闻,我们确实并非每次都要选择“更快”的排序算法,当排序时间不比程序的其它部分(比如输入数据)更慢的话,就没有必要在“更快”的排序上纠结,此时简单的方法或许更为有效。此外,如果排序的是基本有序的文件,那么冒泡排序只要花费很少的代价就能把文件放置到位,对于文件的来说,我们几乎总是认为比较操作远比移动操作耗费的资源更少。由此看来,冒泡排序并没有那么糟糕,不是吗?
作者:我是8位的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号