算法分析(1)——数据的影响和函数的增长

算法分析

　　在编写代码的某一时刻，自然会产生一段代码比另一段代码运行得更快的思想。算法分析的任务便是尽可能多地发现算法的性能特征，以便让程序员利用这些特征做出正确的选择。在分析之前，首先要了解影响算法性能的因素并排除一些混淆视听的干扰项。

数据对性能的影响

　　也许我们都曾经遇到过这种情况，在某一特定的时刻，算法会运行的十分缓慢，经过排查得知，这是由于一些特殊的数据造成的，于是我们针对这批数据精心设计了另一个代替算法，最后得到了一个令人满意的结果。遗憾的是，这种看似令人满意的结果是带有欺骗性的，它忽视了一个问题——输入数据是随机的，这意味着针对精心挑选的数据而选择的新算法并不能真正衡量算法的快慢。这种忽视及其常见，甚至出现于一些知名软件工具的官网上，他们号称自己的工具比竞争对手的运行效率高出某个百分比，当你真正使用时却发现并不是那么回事，至少不像官网上宣称的那样。所以说，精心挑选的数据不利于判断算法的性能，它将使算法偏向好的一侧。

　　由于我们验证的是算法而不是数据，一个较为理想的方法是直接使用生产数据，它能让我们确切地衡量算法在真实环境中的开销。然而生产数据通常是软件正式运行一段时间后积累产生的，在构建软件的阶段很可能与实际生产脱节，这就迫使我们使用自行创造的随机数据。随机数据能够表现出程序中平均状态下的性能，让我们在开发和测试阶段能够选择一个较为靠谱的算法。

　　值得注意的是，随机数据是实验室的结果，并不能代表程序的实际运行效率，我们可以把自行创造的数据和真实数据分别输入程序，对比它们的运行结果，看看试验和真实环境是否匹配，如果匹配，说明我们的选择或改进是正确的；否则需要进一步分析数据对算法的影响。

　　最后是创造最坏的数据，研究程序中极端情况下的性能。某一些算法可能会对输入极端敏感，它们的性能会随着数据的改变而跌宕起伏，比如插入排序，这也迫使我们在选择算法时需要充分考虑输入的数据。虽然最坏的数据可能永远都不会发生，但它们仍然提供了关于性能的重要信息。

　　一个关于数据选择的陷阱是过于强调极端情况下的坏数据。由于大多数算法的运行时间都取决于输入，于是一种自然的倾向就产生了——选择一种尽可能小地依赖输入数据的算法，这个目标让我们对最坏的输入数据着迷。然而，能够提高极端情况效率的算法实现起来可能极为复杂；更尴尬的是，拼尽全力实现的算法虽然能够获得极端情况下的性能提升，但在生产环境下却比一个简单的算法更慢，这使得我们不得不考虑新算法是否真的有效，或者它能够提高的性能是否值得付出。

影响性能的其它因素

　　不同的机器、操作系统、编程语言、网络都将对算法造成影响，在资源共享的环境中，甚至相同的程序在不同的时间也会表现出不同的性能。也许一个运行缓慢的程序只需要为机器增加内存就可以解决。

　　当程序中参杂了过多不可预估的开销时，可能会导致运行效率不可预估地下降。一个典型的场景是对内存的漠视，这常见于企业级应用中：某个程序需要根据一批订单号从数据库中获取一些数据进行处理，大多是时候，较为快速的方法是一次性从数据库中加载这些数据，然后在内存中处理，而不是多次请求一条数据，一次加载法将节省数据库请求和网络连接的开销。遗憾的是，数量惊人的系统中都在使用循环，每次只获取一条数据。

　　由于存在会影响算法性能的一系列不确定因素，所以精确预测某个程序的运行时间似乎是不可能的，但好消息是我们能够得到一个大致的轮廓，或者知道这某种特定情况下，一个算法比另一个更快。

　　算法分析的一个重要步骤是把抽象操作和实际运行分开，以下面的代码为例：

　　for i in range(n):

　　　　sum += i

　　一共执行了多少加法运算是抽象操作，它是由算法的性能决定的；而这段代码实际运行了多久是由具体的计算机决定的。将二者分开有助于我们独立于特定的编程语言或计算机分析算法。

　　此外还要抛弃的是内存、网络、数据库等共享资源，也就是说，我们重点度量的是“计算”，是理想中世界，是物理中的光滑平面。

运行比较法

　　在蛮荒时代，我们通过一种毫无神秘性可言的方法比较两个算法的快慢：对于解决同一个问题的两个算法，分别运行一下，看哪个运行的时间更长。这个方法直接而暴力，似乎于根本不值得一提，然而在实际应用中，它将遇到两个难题，以至于“运行比较法”在很多时候都令人沮丧。

　　第一个难题是，对于某些复杂的算法来说，编写一个能够正确的、完整运行的实现将是一个巨大的挑战，编写新实现所花费的代价甚至可能远远超出了问题本身，以至于一开始就让人心生恐惧——特别是在经历了一系列苦难完成了实现后，却发现运行时间比原来更慢，这将严重影响士气。

　　另一个难题是等待时间可能太长。如果待处理的问题本身就过于复杂，即使一个高效的算法也需要运行很长时间。对于一个运行时间是10秒的算法，或许不难注意到比它快10倍的改进版；但是对于一个运行时间以天为单位的方法，即使快上10倍，也需要超过2两小时。对于两个已经存在的程序，如果需要花小时级的时间才比较出它们谁快谁慢的结论，那么几乎可以肯定这不是一种有效的方法。

数学分析法

　　运行比较法的困难迫使我们求助于数学分析，虽然我们不能对一个还没有实现的程序使用运行比较法，但却能通过数学分析了解程序的性能并预估改进版本的有效性。

　　大多数算法都有影响运行时间的主要参数N，这里的N是所解决问题的大小的抽象度量，对于一个排序算法来说，N是待排序文件的大小或列表中的元素个数。我们的目标是尽可能地使用简单的数学公式，用N表达出程序的运行时间。

函数的增长

　　对于将要比较的两个算法，我们并不满足于简单地描述为“一个算法比另一个算法快”，而是希望能够通过数学式表达直观地感受到二者具体的差异。

　　一些函数在算法分析中极为常见：

　　1

　　如果程序中的大多数指令只运行一次或几次，与问题的规模无关，我们就说程序运行的时间是常量的。小高斯的算法就是典型的常量时间。

　　logN

　　随着问题规模的增长，程序运行时间增长较慢，可以认为程序的运行时间小于一个大常数。对数的底数会影响常数的值，但影响不大。如果底数取10，当N=10000时，logN=4；当N增长了十倍时，logN=5，仅有略微的增长；只有当N增长到N²时，logN才翻倍。如果一个某个算法是把一个大问题分解为若干个小问题，而每个小问题的运行时间是常数，那么我们认为这个算法的运行时间是logN，二分查找就是一个典型。由于计算机是二进制的，所以通常用2为底的对数作为计算机中最“自然”的对数。

　　

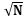
　　比logN稍大，当问题规模翻倍时，运行时间比翻倍少一点；当N增长100倍时，程序运行时间增长10倍。开销是 时间的程序通常对程序的终止条件做了处理，比如1.3.2节中的is_prime_2方法用来判断N是否是素数，程序的边界是N^1/2，而不是N。

　　N

　　这就是通常所说的线性时间，如果问题规模增大了M倍，程序运行时间也增大M倍。1到100的蛮力求和法就是线性时间，这类方法通常带有一个以N为终点的循环。

　　NlogN

　　当问题规模翻倍时，如果运行时间比翻倍多一点，我们就简单地说程序运行的时间是NlogN。如果底数取10，当N=10000时，NlogN=40000；如果N翻倍，NlogN≈43000。NlogN与logN都是把一个大问题分解为若干个能过在常数时间内运行的小问题，区别在于是否需要合并这些小问题，如果合并小问题，就是NlogN；如果不需要合并，就是logN。大多数归并问题的运行时间可以简单地看作NlogN。

　　N²

　　如果问题规模翻倍，运行时间增长4倍；问题规模增长10倍，运行时间增长100倍。这类算法只对小规模的问题起作用。

　　N³

　　如果问题规模翻倍，运行时间增长8倍；问题规模增长10倍，运行时间增长1000倍。

　　2^N

　　真正要命的增长。如果N=10，2^N=1024；N翻倍后，2^N=1048576。复杂问题的蛮力法通常具有这样的规模，这类算法通常不能应用于实际。

　　这些函数能够帮助我们直观地理解算法的运行效率，让我们很容易区分出快速算法和慢速算法，大多数时候，我们都简单地把程序运行的时间称为“常数”、“线性”、“平方次”等。对于小规模的问题，算法的选择不那么重要，一旦问题上了规模就，算法的优劣就会立马体现出来。下面的代码展示了当问题规模是10、100、1000、10000、100000、1000000时log₂N、N^1/2、N、log₂N、N²、N³的增长规模：

import math
# 函数列表
fun_list = ['log2N', 'sqrt(N)', 'N', 'Nlog2N', 'N^2', 'N^3']
print(' ' * 10, end='')
for f in fun_list:
    print('%-15s' % f, end='')
print('\n', '-' * 100)
# 问题规模
N_list = [10 ** n for n in range(1, 7)]
for N in N_list:
    print('%-8s%-2s' % (N, '|'), end='')
    print('%-15d' % round(math.log2(N)), end='')
    print('%-15d' % round(math.sqrt(N)), end='')
    print('%-15d' % N, end='')
    print('%-15d' % round(N * math.log2(N)), end='')
    print('%-15d' % N ** 2, end='')
    print(N ** 3)

　　打印结果:

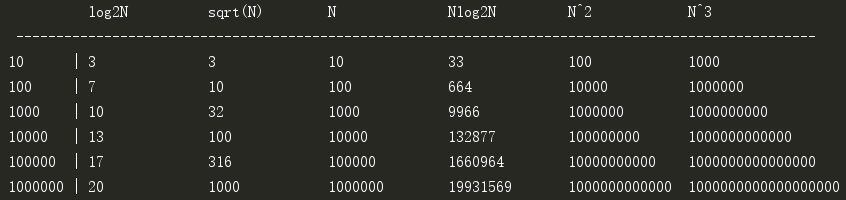
　　2^N增长的太过迅猛，作为一个另类单独列出：

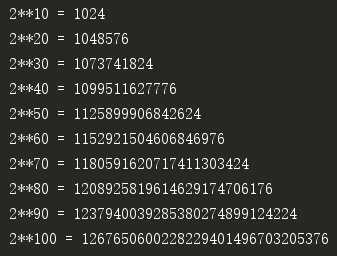
　　这些打印结果告诉我们，有些时候，选择正确的算法是解决问题的唯一途径。对于函数的输出结果来说，如果把100看作1秒，那么10000就是100秒，超过1分半。这意味着对于一个规模是1000000的问题来说，一个效率是logN的算法可以立刻得出结果，效率是 的算法耗时约10秒，效率是N的算法耗时将超过2.5小时，N²则需要300多年！也许我们可以忍受一运行10秒或2.5小时的程序，但一定没法容忍有生之年看不到结果的程序。

　　最后再来看一下这些函数的增长曲线

　　

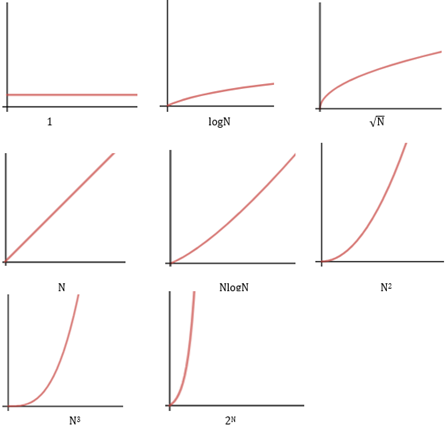
算法选择的陷阱

　　如果不理解函数的增长，可能会忽视算法的性能。由于较为快速的算法往往比蛮力法复杂得多，所以多数程序员们通常更愿意使用虽然慢一点但是更加直接的算法；但是有些时候，只要加上少许的代码就能让程序的效率提升——整数的故事中is_prime_2方法对于判断素数的改进——此时仍然使用蛮力法就不那么合适了。

　　当我们迫不及待地使用函数增长的知识改进算法时，另一个陷阱也张开了大口——如果一个程序的运行时间相当短暂，却仍然试图花费大量时间提高它的运行效率，这就没什么意义了，特别是当你预计这段低速的程序只会运行几次时。如果你这么做了，那么你就是把时间浪费在不重要的问题上，花了大量时间试图改进程序的整体性能，但实际上却根本没有改进。

　　这两个陷阱的一个关键是问题的规模，对于1加到100的问题，也许我们使用循环累加法无伤大雅；但是当累加的终点不确定但及可能存在一个大终点时，就更应该选择小高斯的方法。由此看来，在很多时候算法也没有泛泛的好坏之分，只有在特定问题下的合适与不合适。

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”