线性代数笔记23——矩阵的对角化和方幂

特征值矩阵

　　假设A有n个线性无关的特征向量x₁,x₂……x_n，这些特征向量按列组成矩阵S，S称为特征向量矩阵。来看一下A乘以S会得到什么：

　　最终得到了S和一个以特征值为对角线的对角矩阵的乘积，这个对角矩阵就是特征值矩阵，用Λ表示：

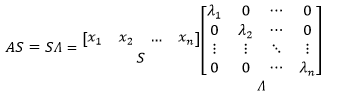
　　没有人关心线性相关的特征向量，上式有意义的前提是S由n个线性无关的特征向量组成，这意味着S可逆，等式两侧可以同时左乘S^-1：

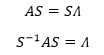
　　AS=SΛ和S^-1AS=Λ就是对角化的两种方法。需要注意的是，并非所有矩阵A都存在n个线性无关的特征向量，这类矩阵不能对角化。

　　矩阵对角化还有另一种表达：

　　我们已经知道了矩阵的LU分解，A=LU；格拉姆-施密特正交化，A=QR；现在又多了一种对角化分解，A=SΛS^-1

矩阵的方幂

　　如果A存在特征值和特征向量，即Ax = λx，那么A²的特征值和特征向量是什么？

　　这在上一章的示例中出现过，将Ax = λx的等式两侧同时左乘A就可以表示A的特征向量：

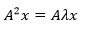
　　由于λ是标量，所以可以把λ单独提出来：

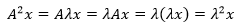
　　现在可以得出结论了，A²的特征向量不变，特征值变成了λ²

　　可以用同样的方式看看A²的对角化：

　　按照这个思路可以继续计算A^k的对角化，A^k的特征向量不变，A^k的特征值矩阵是A的特征值矩阵的k次方：

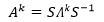
　　根据上式，如果k→∞，在所有特征值|λ_i|<0时，A^k→0，当然，前提是A有n个线性无关的特征向量。

对角化的前提

　　对角化的前提是A存在n个线性无关的特征向量，问题是怎样判断A存在n个线性无关的特征向量？一个判断方法是：当A的所有特征组互不相同时，A必然存在n个线性无关的特征向量；如果存在重复的特征值就不好说了，需要另行判断。

　　n阶单位矩阵的所有特征值都是1，但是它仍然有n个线性无关的特征向量，因此单位矩阵可以对角化：

　　再来看三角矩阵。三角矩阵A的各列是线性无关的，意味着它有唯一解，没有n个线性无关的特征向量，比如下面这个：

　　先计算A的特征值：

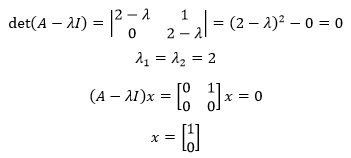
　　作为2×2矩阵，A只有一个特征向量，它无法完成对角化。

使用对角化

　　给定一个向量u₀和一个能够对角化的矩阵A，如果u_k+1=Au_k，那么u₁₀₀ = ?

　　可以简单的向后推导一下：

　　现在可以得到结论，u₁₀₀=A¹⁰⁰ u₀，问题是如何求得A¹⁰⁰？

　　A有n个线性无关的特征向量x₁,x₂,……,x_n，这意味着u₀可以看成这些特征向量的线性组合：

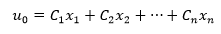
　　以单位矩阵为例，假设A是3×3的单位矩阵，则A的三个特征向量是：

　　这三个特征向量可以通过线性组合成为任意的三维向量。

　　现在可以将Au₀写成下面的形式：

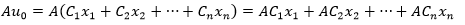
　　由于C_i是标量，所以可以将C_i写到前面：

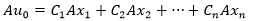
　　x₁,x₂,……,x_n都是A的特征向量，它们以特征值为媒介和A存在关联，Ax_i = λ_ix_i，因此：

　　等式两侧同时左乘A：

　　同样，可以把比标量C_iλ_i放到前面：

　　无论等式两侧再左乘几个A都将得到类似的结果，因此：

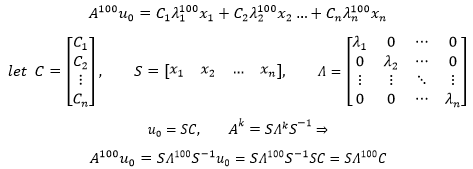
　　这就是最终的答案，如果真要计算A¹⁰⁰ u₀，可以先把u₀展开成特征向量的线性组合，求出具体的C值，在使用SΛ¹⁰⁰C求解。

综合示例

　　

　　a,b都是0的时候没什么可算的，主要看ab≠0的情况。C看起来比较别扭，还是用A来说话。先来看一下特征值：

　　特征值矩阵和特征向量矩阵是：

 

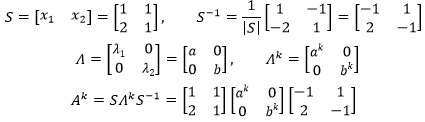
　　当a=b=-1时：

 

---

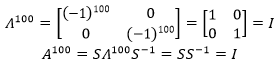
　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”