线性代数笔记21——伴随矩阵和克莱姆法则
伴随矩阵
对于2×2矩阵来说，它的逆矩阵公式：
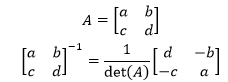
对于更高阶矩阵，我们也希望使用类似的公式。从2×2的逆矩阵公式可以看出，它的逆矩阵由两部分组成，其一是行列式的倒数，这意味着矩阵可逆的前提是行列式不为0，问题是另一部分是什么？
仔细观察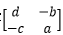
，发现它和代数余子式有一定的关系，对于A来说：
a的代数余子式：
b的代数余子式：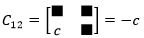
c的代数余子式：
d的代数余子式：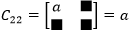
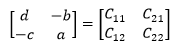
上一节提到过代数余子式的正负号与行列号之和有关，和是奇数，代数余子式是取负号，和是偶数取正号。
由此一来，A的逆矩阵就等于A的行列式的倒数乘以某个由代数余子式组成的矩阵：
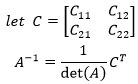
上式中的CT就是原矩阵A的伴随矩阵，它是由A衍生而来的。由于转置的缘故，伴随矩阵中的Cij就是原矩阵中Cji的代数余子式。
克莱姆法则
现在把逆矩阵的公式应用到方程中：
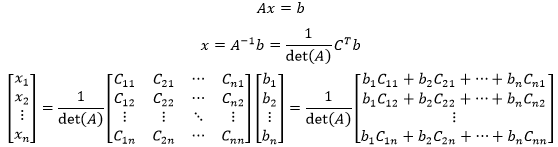
似乎有些杂乱无章，进一步看x的每一个分量，会发现x的各个分量都包含A中某列元素的代数余子式。以x1和x2为例：
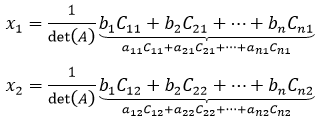
x1相当于将det(A)按照第一列展开，x2相当于将det(A)按照第二列展开，只不过把它们的展开列替换成了b，相当于：
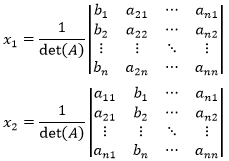
将x1和x2后面的行列式分别按第1列和第2列展开成代数余子式，就得到了每一个分量的结果。这就是克莱姆法则，也叫克拉默法则。
克莱姆法则有一种常用的记法，在Ax = b中，未知数的系数构成了系数行列式D：
若线性方程组的系数矩阵可逆（非奇异），即系数行列式 D≠0，则线性方程组有唯一解，其每一个分量的解为：
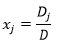
其中Dj是把D中第j列元素对应地换成b中的元素而其余各列保持不变所得到的行列式，比如：
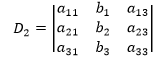
克莱姆法则为方程组的解提供了一个代数表达式，让你能使用代数运算，而不只是写算法，但是如果真的用它来解方程将变成一个灾难，因为你必须对n+1个行列式求值。克莱姆法则研究了方程组的系数与方程组解的存在性与唯一性关系。与其在计算方面的作用相比，克莱姆法则更具有重大的理论价值。
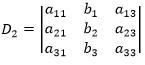
作者：我是8位的
