Linear Feedback Shift Register
LFSR can be drawn in the following style.
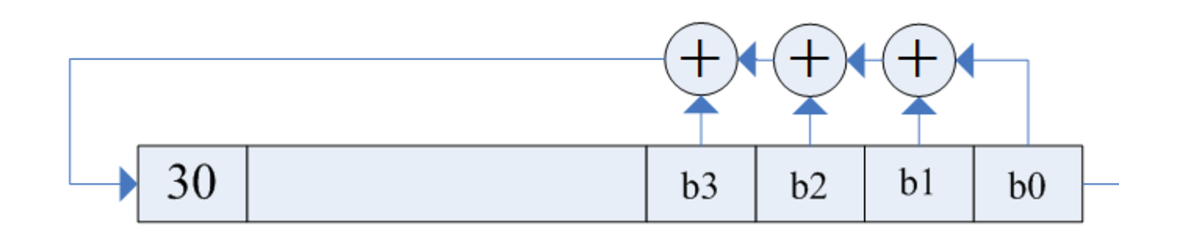
The above figure can be descripted as mod2(b(n+31) = b(n+3) + b(n+2) + b(n+1) + b(n)).
Now my question is if I give an initial state S0 {b30, b29, …., b2, b1, b0}, how can I get the value starting from Nc=1600 to Nc + 30.
clear;
clc;
// initial state
b(1:31)=0;
b(2) = 1;
b(8) = 1;
b(13) = 1;
b(14) = 1;
// derive the following state
for i=32:1631
b(i) = mod(b(i-31) + b(i-30) + b(i-29) + b(i-28), 2);
end
b(1601:1631)
Yes. It seems simple and easy. But in a run-time environment, we will run dummy Nc step. Next, I will use the transfer matrix to do this simple question.
Consider we want state S1 {b31, b30, …, b2, b1} which is only one step after initial state. We can use a 31*31 transfer matrix P to derive it.
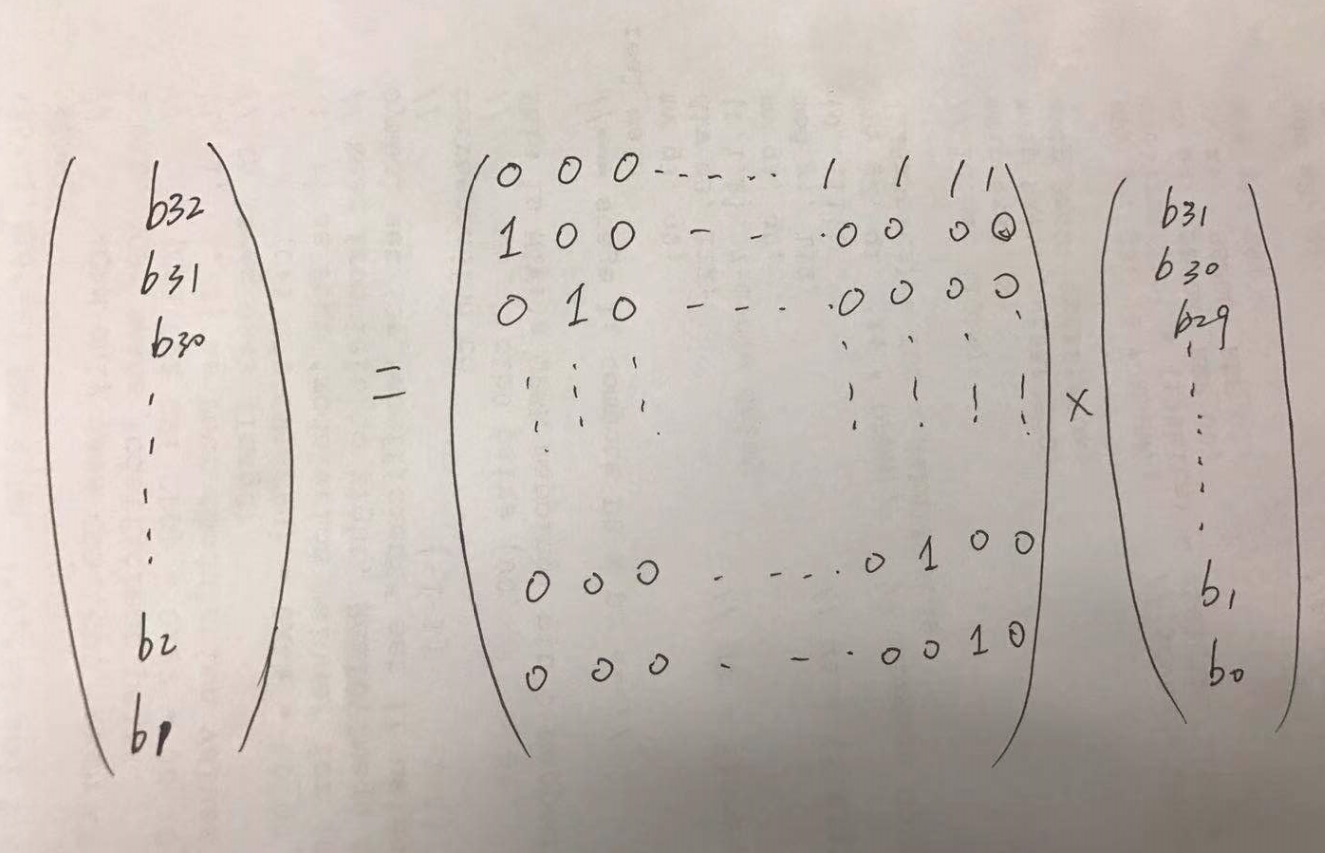
So we know S1 = P * S0. Hence, recursively, we know S2 = P * S1 = P * P * S0, …., Sn= P * P * ….*P * S0.
function [p] = genLSFR_Step(num_steps, transfer_func)
% create init transfer matrix
transfer_matrix = zeros(31, 31);
transfer_matrix(1, :) = transfer_func;
for (i = 2:31)
transfer_matrix(i, i-1) = 1;
end
% derive transfer matrix afer steps
if (num_steps == 1)
p = transfer_matrix;
return;
else
p = transfer_matrix;
for (i = 1:(num_steps-1))
p = mod(p * transfer_matrix, 2);
end
end
return;
The P matrix can be pre-calculated and in the real time, only one matrix multiplication is needed.



