基于改进人工蜂群算法的K均值聚类算法(附MATLAB版源代码)
其实一直以来也没有准备在园子里发这样的文章,相对来说,算法改进放在园子里还是会稍稍显得格格不入。但是最近邮箱收到的几封邮件让我觉得有必要通过我的博客把过去做过的东西分享出去更给更多需要的人。从论文刊登后,陆陆续续收到本科生、研究生还有博士生的来信和短信微信等,表示了对论文的兴趣以及寻求算法的效果和实现细节,所以,我也就通过邮件或者短信微信来回信,但是有时候也会忘记回复。

另外一个原因也是时间久了,我对于论文以及改进的算法的记忆也越来越模糊,或者那天无意间把代码遗失在哪个角落,真的很难想象我还会全力以赴的还原当年代码的真相。
所以还是决定通过这篇文章,让需要的人主动获取吧,当然如果有更细节的问题也欢迎交流。
首先,简单介绍下相关的概念和背景知识
聚类
聚类,一种无监督学习,是数据挖掘领域的一个重要研究方向。聚类就是将数据对象分组成多个簇(类),同一簇内的对象相似度尽可能大,不同簇间的对象相似度尽可能小。
K-means算法
K-means即K均值是一种基于划分思想的聚类算法,它是聚类算法中最经典的算法之一,它具有思路简单、聚类快速、局部搜索能力强的优点。但也存在对初始聚类中心选择敏感、全局搜索能力较差、聚类效率和精度低的局限性问题。类似这种K-means算法在各行各业都会有自己的应用场景,比如我在毕业论文中有提到的基于改进算法的社区划分。
群体智能与仿生算法
群体智能与仿生算法,以其进化过程与初始值无关、搜索速度快、对函数要求低的优点,成为进化算法的一个重要分支,并吸引了各个领域学者对其研究。目前,比较常见的群体智能与仿生算法有粒子群算法(PSO)、细菌觅食算法(BF)、人工鱼群算法(AFSA)、遗传算法(GA)、蚁群算法(ACA)等
人工蜂群算法
Seeley于1995年最先提出了蜂群的自组织模拟模型,在该模型中,虽然各社会阶层的蜜蜂只完成了一种任务,但是蜜蜂以“摆尾舞”、气味等多种方式在群中进行信息的交流,使得整个群体可以完成诸如喂养、采蜜、筑巢等多种工作。Karaboga于2005年将蜂群算法成功应用于函数的极值优化问题,系统地提出了人工蜂群算法(Arificial Bee Colony, ABC),该算法简单、全局搜索能力好、鲁棒性强。但是,人工蜂群算法也存在着后期收敛速度较慢、容易陷入局部最优的问题。
算法的改进思路
鉴于K-means算法和人工蜂群算法各自特性,提出一种基于改进人工蜂群的K-means聚类算法IABC-Kmeans。该算法首先对人工蜂群算法进行改进:利用提出的最大最小距离积法初始化蜂群,保证初始点的选择能够尽可能代表数据集的分布特征;在迭代过程中使用新的适应度函数和位置更新公式完成寻优进化。然后将改进后的人工蜂群算法应用到K-means算法中完成聚类。
改进算法IABC的流程图如下
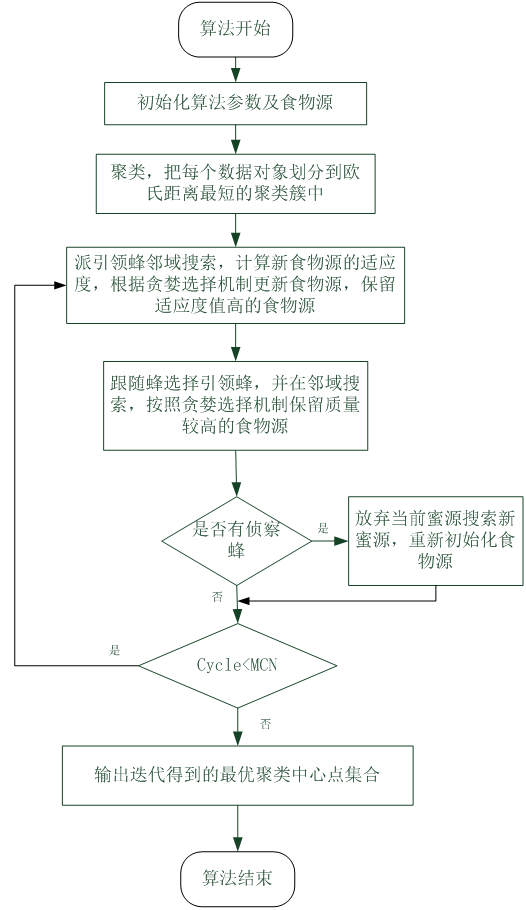
改进算法IABC的验证和效果展示
使用改进算法在Sphere、Rastrigin、Rosenbrock和Griewank四个测试函数上测试

迭代收敛的效果如下
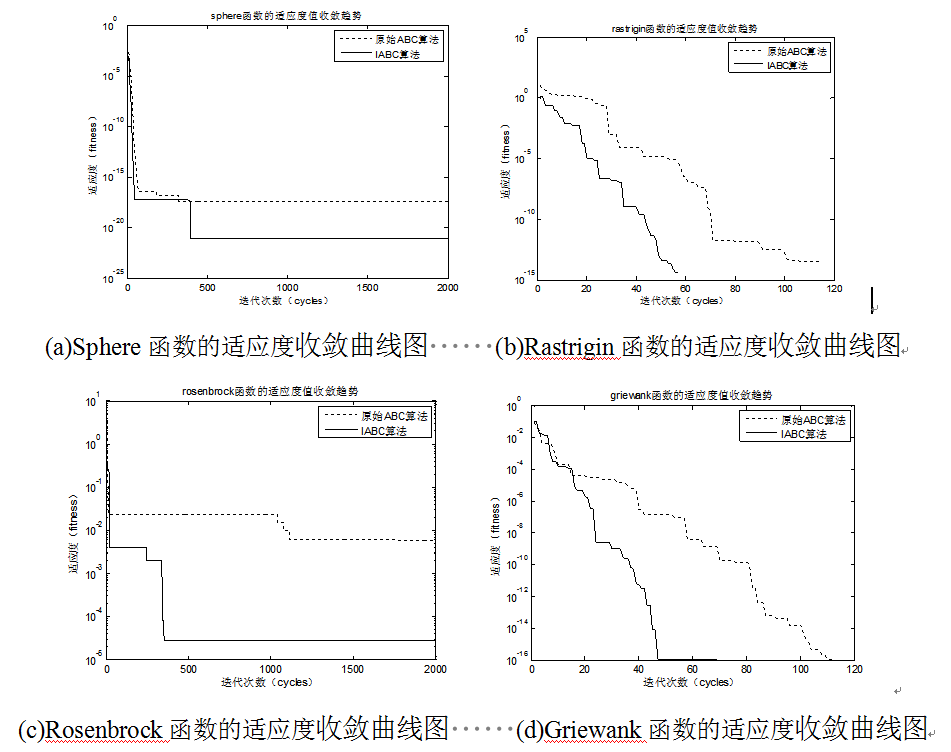
从图(a)-图(d)可以看出,原始ABC算法在四个标准测试函数上迭代寻优过程中都遇到了不同程度的迭代收敛速度缓慢和陷入了局部极值的情况,从(b)和(d)可以看出在达到相同局部最优解的过程中,原始ABC算法需要的经历更多次的迭代和较长的迭代时间花销;从(a)和(c)的适应度变化趋势可以发现,原始ABC算法在搜索最优解的精度和准确度上表现能力不足,改进前后的最优解相差好几个数量级。相比于原始ABC算法,改进后的ABC算法由于加入有目的性的初始化过程,并引入了全局引导因子,所以在迭代寻优搜索过程中,不论是单峰函数还是多峰函数,在搜索精度和收敛速度上明显高于原始ABC算法,体现了改进的有效性。
为了更好的体现改进算法的优越性,除了与原始ABC算法进行纵向比较,下面还将本文算法与文献[32](一种结合人工蜂群和K-均值的混合聚类算法)中的同类改进算法进行横向对比。原始ABC算法、文献[32]算法以及IABC算法在四个标准函数上的适应度变化趋势如图所示
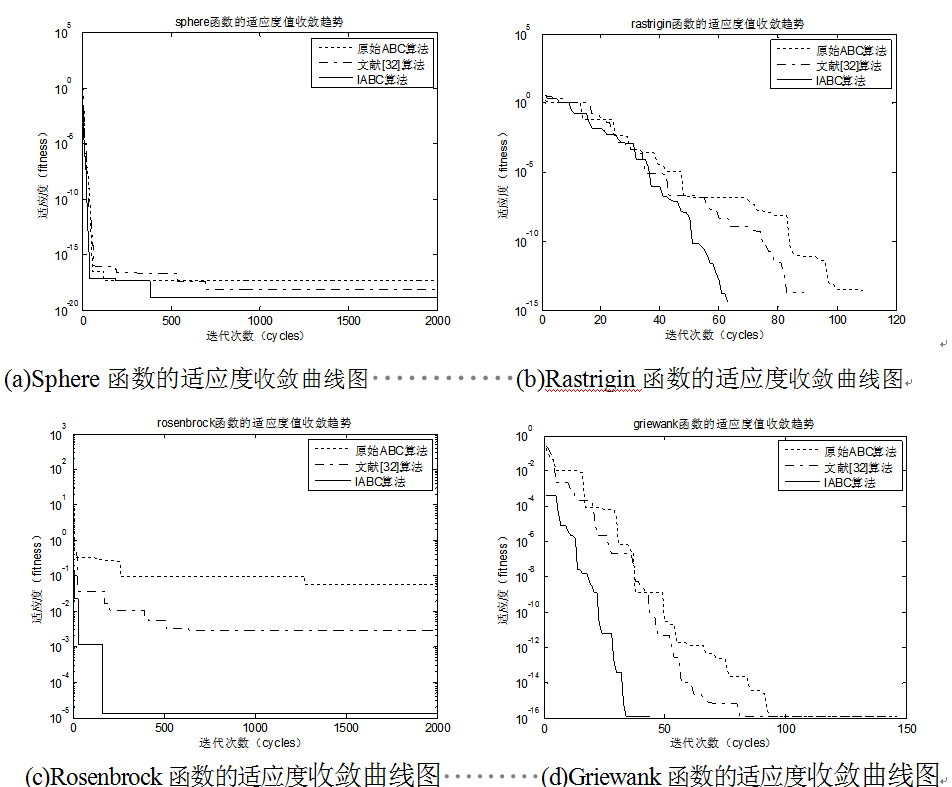
改进算法IABC-KMC的验证和效果展示
算法的参数设置如下
|
参数名称 |
数值 |
|
最大迭代次数 |
100 |
|
蜂群规模 |
20 |
|
Iris数据集聚类个数k |
3 |
|
Balance-scale数据集聚类个数k |
3 |
|
Glass数据集聚类个数k |
6 |
|
最大开采次数Limit |
10 |
K均值算法、ABC+KMC算法、文献[32]算法以及IABC-KMC算法在数据集上的分别测试验证并作对比分析,实验中相关指标如下表所示。
Iris数据聚类对比结果
|
算法名称 |
最差值 |
最优值 |
平均值 |
标准差 |
|
K均值 |
2.9545 |
4.4347 |
4.3096 |
1.4410 |
|
ABC+K均值 |
3.9517 |
4.5563 |
4.4554 |
0.0973 |
|
文献[32]算法 |
4.0694 |
4.6925 |
4.6432 |
0.0105 |
|
本文算法 |
4.7355 |
4.8095 |
4.8058 |
0.0011 |
Balance-scale数据聚类对比结果
|
算法名称 |
最差值 |
最优值 |
平均值 |
标准差 |
|
K均值 |
0.4262 |
1.1874 |
0.9761 |
1.7460 |
|
ABC+K均值 |
0.9075 |
1.2835 |
1.2442 |
0.0608 |
|
文献[32]算法 |
0.9488 |
1.3254 |
1.3059 |
0.0183 |
|
本文算法 |
1.1203 |
1.3337 |
1.3271 |
0.0034 |
Glass数据聚类对比结果
|
算法名称 |
最差值 |
最优值 |
平均值 |
标准差 |
|
K均值 |
5.6381 |
10.1543 |
8..6487 |
2.0293 |
|
ABC+K均值 |
7.8429 |
10.6544 |
9.9501 |
0.3741 |
|
文献[32]算法 |
7.7624 |
10.7215 |
10.6855 |
0.1626 |
|
本文算法 |
10.8526 |
11.8919 |
11.8897 |
0.0582 |
在上面三个表数据中,可以发现K均值算法聚类的标准差相对较大,容易陷入局部极值,全局寻优能力较弱,而且趋于稳定值所需的迭代次数多、耗时长,主要是因为K均值算法对于初始点选择比较敏感并容易陷入局部极值。ABC+KMC算法相较于K均值算法,标准误差有所减小,但由于原始ABC存在易早熟的不足,所以算法出现了后期收敛速度缓慢,耗费时间较长,常停滞于局部最优的情况。文献[32]算法通过引入了线性调整策略从而能够快速定位到最优解,但是全局搜索能力仍不突出,早熟问题很难避免。IABC-KMC算法具有较强的全局搜索能力特性,从而能够跳出局部极值,得到质量更高的解,所需迭代次数更少,收敛速度和聚类精确度都有显著提升,且整个迭代过程中标准差最小。
综上看来,IABC算法通过在四个测试函数上实现,发现不论是在效率还是准确率上都比原始ABC算法和文献[32]算法要高,解决了算法存在的易陷入局部极值和迭代后期收敛速度缓慢问题,提高了算法的健壮性和整体性能。IABC-KMC算法通过融入IABC算法与K均值算法,优势互补,增强了整个聚类过程的稳定性。
Github:https://github.com/DMinerJackie/IABC-KMC
1.代码中几乎每一行都有自己的注释,参看算法的思想和步骤再来看应该不难
2.相应的测试函数以及测试数据集也一并上传(Iris,Balance-scale,Glass),程序中写的是绝对路径,需要自己改下
3. 如果大家对此感兴趣,还将出一篇基于该改进算法的社区检测的介绍
怀恋当初写这篇论文的时候,从确定思路,到下载相关论文,再到代码编写以及实验数据整理以及后来的论文录用,整整花了一个月的时间,记得当时只是从网上down了一个人工蜂群算法原型,期间代码改写,加入改进的点以及调优,直到得到了理想的数据和图表,那是一段充实的时光,难忘的岁月,写在2017年第一天也是激励自己,不忘初心,砥砺前行!
如果您觉得阅读本文对您有帮助,请点一下“推荐”按钮,您的“推荐”将是我最大的写作动力!如果您想持续关注我的文章,请扫描二维码,关注JackieZheng的微信公众号,我会将我的文章推送给您,并和您一起分享我日常阅读过的优质文章。
友情赞助
如果你觉得博主的文章对你那么一点小帮助,恰巧你又有想打赏博主的小冲动,那么事不宜迟,赶紧扫一扫,小额地赞助下,攒个奶粉钱,也是让博主有动力继续努力,写出更好的文章^^。
1. 支付宝 2. 微信





 浙公网安备 33010602011771号
浙公网安备 33010602011771号