01背包问题

1.背包问题

(1)问题由来：给定n个重量为w1,w2..........wn，价值为v1,v2........,vn的物品和一个承重为W的背包，求这些物品中最有价值的一个子集，并要求能够装到背包中。这里假设所有的重量和包的承重都是正整数，而物品的总重量不必是整数。

(2)地推公式：为了设计一个动态规划算法，需要推导一个递推关系，用较小实例解的形式来表示背包问题的实例的解。接下来我们来考虑一个由前i个物品定义的实例，物品的重量分别w1,w2,w3,..wi，价值分别为v1,v2,.........vi，背包承受的重量为j(j>=1,j<=w)。设F(i,j)为该实例最优解的物品总价值，也就是说能够放进承重为j的背包中的前i个物品中最有价值自己的总价值。可以将前i个物品中能够放进承重为j的背包中的子集分为两个类别：包括第i个物品的子集和不包括第i个物品的子集。

(3)根据上面的描述有下面的结论：

　　根据定义，在不包括第i个物品的子集中，最优子集的价值为F(i-1,j)。

　　在包括第i个物品的子集中，最优子集是由该物品和前i-1个物品中能够放进承重为j-wi的背包的最优子集组成。这种最优子集的价值为vi+F(i-1,j-w)

(4)因此，在前i个物品中最优解的总价值为两个价值中的较大值。当然如果第i个物品不能够放进背包，则从前i个物品中选出的最优子集的总价值等于从前i-1个物品中选出的最优子集的总价值。这个结果又下面的递推公式。

我们可以比较容易的定义如下的初始条件：当j>=0的时候，F(0,j)=0；当i>=0的时候，F(i,0)=0

我们的目标是F(n,w)，即n个给定的物品中能够放进承受重量为w的背包中的子集的最大总价值以及最优子集本身。当i,j>0的时候，为了计算第i行第j列的单元格F(i,j)，我们拿前一行同一列的单元格与vi加上前一行左边wi列的单元格的和作比较，计算出两者的较大者。

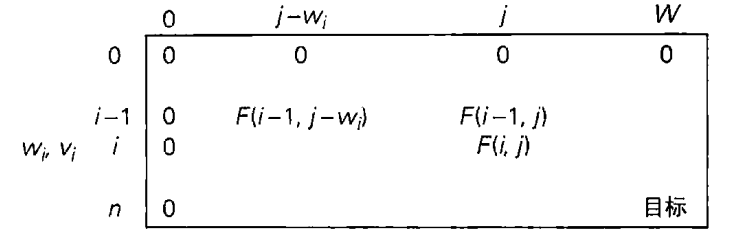
(5)实例：考虑下列数据给出的实例

下图给出了由动态规划公示计算的动态规划表

最大的总价值为F(4,5)=37可以通过上表回溯过程来求得最优子集元素，因为F(4,5)=37,F(3,5)=32，物品4填满背包余下5-2=3个单位承重量的一个最优子集都包括在最优解中。

(6)记忆化

 动态规划所涉及问题的解满足一个交叠子问题来表示递推关系。直接使用自顶向下的这样一个地推关系求解导致算法要不止一次的求解公共子问题，因此算法的效率比较低(一般来说是指数级的)，另一方面经典动态规划是自底向上工作的，它用所有较小的子问题来填充表格，但是每个子问题只解一次，这种方法无法令人满意的一面是，在求解给定问题时，有些较小子问题的解常常不是必须的。所以我们使用记忆法，该方法使用自顶向下的方式对给定问题进行求解，但是还需要维护一个类似自底向上动态规划算法使用的表格。算法思想如下：

 

 2.实例：

 

package com.nowcoder.dp;

import org.junit.Test;

public class Knapsack {
    public static void main(String[] args){

    }

    /**
     *
     * @param val 实例最优解的最大值
     * @param wight 物品的重量
     * @param w 背包容量
     * @return
     */

    public static int knapsack(int[] val,int[] wight,int w){
        int n = val.length;   //物品的总数量
        int[][] v= new int[n+1][w+1];   //创建背包矩阵
        //对于第0行所有的列来说，他们没有选择物品的权利不能选择物品，所以不管背包容量多少，总价值都是0
        for(int col = 0 ; col<= w ; col++){
          v[0][col] = 0;
        }
        //对于第0列所有的行来说，背包容量为0，不能再向背包中放任何物品
        for(int row = 0 ; row <= n ;row++){
            v[row][0]=0;
        }
        /**
         * 接下来填充记录表
         */
        for(int i = 1 ; i <=n;i++){//先一行一行的填充
            for(int j =1 ; j <= w ; j++){  //再在每一行中按列来填充
                if(wight[i-1]<=w){//如果当前物品的重量小于当前背包的重量
                    v[i][j] = Math.max(val[i-1]+v[i-1][w-wight[i-1]],v[i-1][w]);
                }else {//如果当前物品的重量大于当前背包中的重量
                    v[i][j] = v[i-1][j];

                }
            }
        }
        return v[n][w];
    }
    @Test
    public void test(){
        int[] val = {10, 40, 30, 50};
        int[] wight={5, 4, 6, 3};
        int w = 10 ;
        System.out.println(knapsack(val,wight,w));
    }
}