机器学习读书笔记第六章支持向量机(2):对偶问题

1.我们希望通过下式：最小化w的范数来得到最大间隔划分超平面对应的模型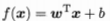，其中w和b是模型参数：

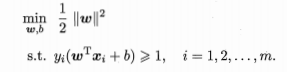
　　这里xi和yi都是已知的，约束条件有m个，每一个样本点有一个约束，有m个样本点有m个约束，w是一个变量，w和b是一个向量。

 2.对上式利用拉格朗日乘子法可以得到其对偶问题，即对上式每条约束添加一个拉格朗日乘子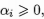，该问题可以写为：

　　

　　上式中第一项是目标函数，后面是利用拉格朗日乘子法。将上述问题转化为求导数为0(求函数极值)的问题：梯度是数值变化最大的方向

　　

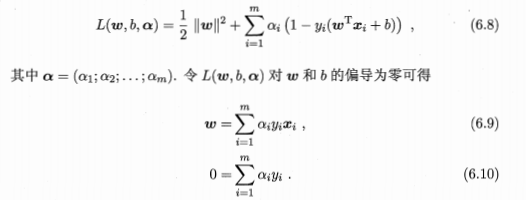
 3.拉格朗日乘子法的几何解释：

　　

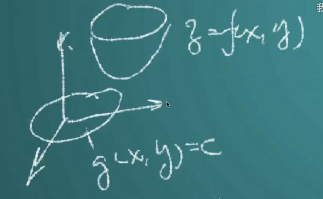
　　约束条件是g(x,y)=c，如果将其投影在平面上面那么看到的就是下面画的这张图，虚线是等高线，

 　　

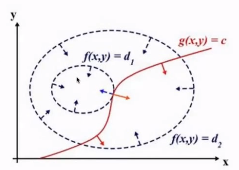
　　在刚接触的时候，约束条件和模型是相切的，垂直于切线的向量是垂直于梯度的，蓝色的向量是在这一点上的梯度，相切要求在同一根直线上。

　4.接下来要求minf(x,y)，约束条件是g(x,y)=c，如果要将其写成拉格朗日函数的话， 那么式子就可以写成：

　　L(x,y)=f(x,y)+λg(x,y-c)

　　那么这个函数取极值的条件是在梯度为0的时候取极值，

 　　

　　

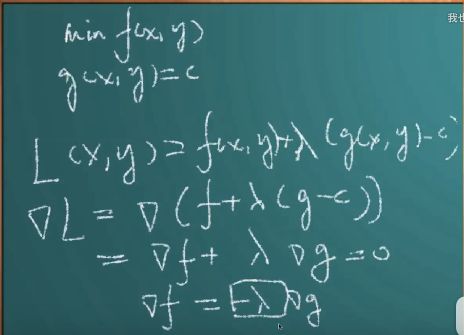
 5.Karush-Kuhn-Tucker最优条件(KKT条件)

　　6.进一步简化为对偶问题

　　　　(1)前一步得出的KKT条件中变量太多，为后续引入核函数模型准备，将前一步的梯度计算结果重新代入到拉格朗日函数，就将w和b消除了

　　　　

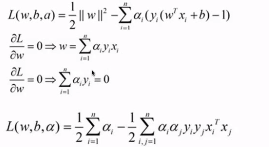
　　　　最后得到的是：有变量的ai和aj的式子。 

　　　　

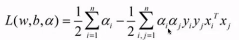
　　　　这就变成了原拉格朗日问题的对偶问题，将求解几何问题变成求解凸优化问题，凸优化问题通过KKT条件变成拉格朗日乘子法问题，把偏导数代进去就可以将拉格朗日乘子法变成一个对偶问题。

　　　　现在这里有一个约束，

　　

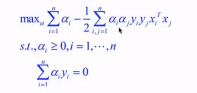
　　如果样本点是支持向量的话，那么αiyi不等于0，其他的不是支持向量的样本点的话αi全部等于0。，

　　在解出α之后，求出w和b，就可以得到模型：

　　　　

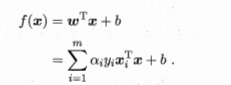
　　上述过程是满足KKT条件的，就是要求：

　　

　　

 

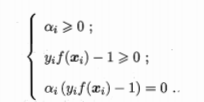
　　　7.线性不可分的情况：松弛变量与惩罚函数

　　　　(1):大部分情况都不是线性可分的，线性不可分的时候无法使用前面的数学技巧，但是可以使用添加惩罚函数的解决方法。

　　　　

　　　　(2)