机器学习读书笔记第六章支持向量机(1):间隔与支持向量

1.分类学习最基本的想法就是：基于一个训练集D在样本空间中找到一个划分超平面，将不同的类别样本分开。两类训练样本“正中间”超平面所产生的结果是最鲁棒的，对局部扰动容忍最好，对于未见的实例的泛化能力最强。

2.划分超平面可以由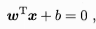：方程来描述，其中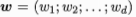为法向量，决定了超平面的方向，b为位移项，决定了超平面与原点之间的距离，划分超平面可以由法向量w和b决定，样本空间中任意一点x到超平面(w,b)之间的距离可以写为：

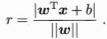
　　对于样本集中的(xi,yi)，若yi=+1，则有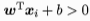，若yi=-1，则有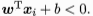，令：

　　

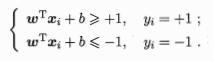
3.如下图所示，距离超平面最近的几个训练样本点使得等号成立，这三个样本点称为“支持向量”，两个异类支持向量到平面的距离之和为：

　　   

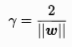
　　　这个量也称之为“间隔”

　　

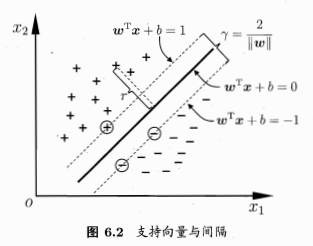
3.要找到“最大间隔”的划分超平面，就是要找到能满足上式中的约束参数w和b使得γ最大：

　显然为了最大化间隔，只要使得1/||w||最大化，就是使得最小化||w||^2，即：

　

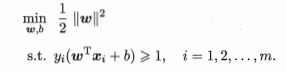
　　这就是支持向量机SVM的基本型