吴恩达机器学习：104核函数(1)

ki一、在这次课程中，我们将改造支持向量机算法，来构造比较复杂的非线性分类器，主要的技巧是称之为核(kernel)的东西，接下来我们看看核函数是什么以及如何使用它。

　　1.如果有一个这样的训练集，然后希望拟合一个非线性判别边界来区分正负样本示例，可能是下面这样的一个边界：一种方法是构造一个复杂多项式特征的集合，也就是像这样一个特征变量的集合，于是就得到一个假设x，得到下右边面式子，

 

　　

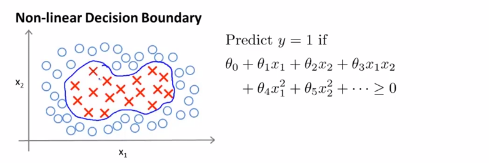
 　　为了说明一种写法，先引入一种会用到的新符号，我们可以把假设函数看成是用下式计算的决策边界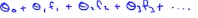，，我们用几个新符号即f1，f2，f3等等来表示新的特征变量，所以f1=x1，f2=x2，f3=x1x2，f4=x1^2，f5=x2^2等等以此类推，但是我们可以有很多不同的特征选择，或者存在比这些高阶的多项式很好的特征，因为我们并不清楚的知道，这些高阶项是不是我们真正需要的，当我们谈到计算机图像的时候，都是由一个大量像素组成的图像，我们也见到过高阶的多项式，运算量将会非常的巨大，高阶多项式的计算很消耗计算资源。

　　2.我们可以用来嵌入到不同的高阶多项式中去，有一个可以构造新特征的方法，高斯kernels函数(相似度函数)  k(x,l(i))，那么看一下核函数到底在做什么：

　　

　　在x特征下，在l(1),l(2)和l(3)的条件下计算显得特征，假设我们只是手动选取这三个点，这些点叫做标记，即我们所说的标记1，标记2，标记3。我们要做的是像这样的定义新特征，给定一个实例x，让我们将第一个特征的定义定义为：

 　　

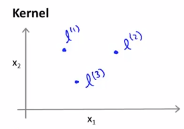
　　接下来我们将第一个特征f_1定义为一种相似度的度量，即度量训练样本x与第一个标记的相似度，这个我们用于相似度的度量，这个特殊的公式是这样的，||x||表示样本x的长度，||x-l(1)||表示欧氏距离取平方，就是点x与标记l之间的欧氏距离

　　(第一个特征)

　　第二个特征就是相似度函数，被定义为度量l(2)和x之间有多相似，那么这个f就被定义为如下的相似函数：其中e是负数

　　

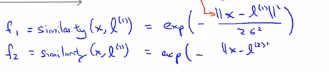
　　同理f3是被定义为x与l(3)之间的相似度。相似度函数就是一个核函数，即高斯核函数。

　　

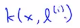
　　相似度函数就是高斯核函数，术语就是这样，概括起来就是这些不同的相似度函数就是核函数，我们可以有不同的相似度度量的函数，上面给的例子是高斯核函数，接下来看看和函数到底做了一些设么，为什么相似度函数的表达式是有意义的？kernels和相似度函数，x和l(1)之间的相似度表示如下：

　　

　　这是向量x和l之间元素对应的距离，在这部分中，我们暂时忽略x0，暂时先不管截距项x0，现在知道如何计算x和标记之间的相似度，接下来看看这个函数做了什么？假设x和其中一个标记点非常接近，那么这个式子的欧氏距离以及分子式之间就会接近0，所以特征f接近于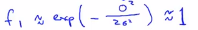：，相反的，如果x和l(1)距离很远，那么特征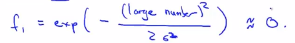，接下来画特征图。

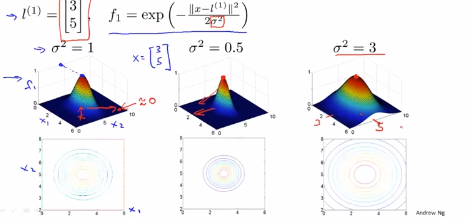
　　eg1:假设有特征变量x1和x2，假设有第一个标记l(1)位于[3,5]，现在假设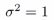，纵轴就是这个曲面的高度，f1的值是横轴，

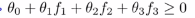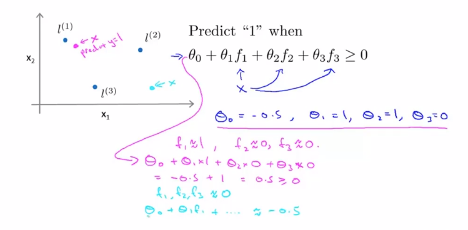
　在看完了特征的定义，　接下来看看能得到什么样的预测函数，给定一个训练样本x，我们要计算出三个特征变量，f1,f2和f3，预测函数的预测值将会等于1，如果，我们假定已经找到了一个学习算法，并且假定我们已经找到了参数的值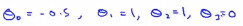，，如果我们有一个训练集，它的左边正好是洋红的点，假定有如下的预测函数x，我们想知道预测函数会给出怎样的预测结果，